
курсовая работа / полиномы лагранжа (масштабирование + оценка погрешности)
.docxМедведев Г.Н. гр.9587
Функция:
x=2*cos(2*T)+2*sin(sqrt(2)*T), T [27pi;28pi]
[27pi;28pi]
Нормированная функция: 2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi)), t [-1;1]
Описание сигнала по Лагранжу
Полином Лагранжа 0 порядка:


Полином Лагранжа 1 порядка:
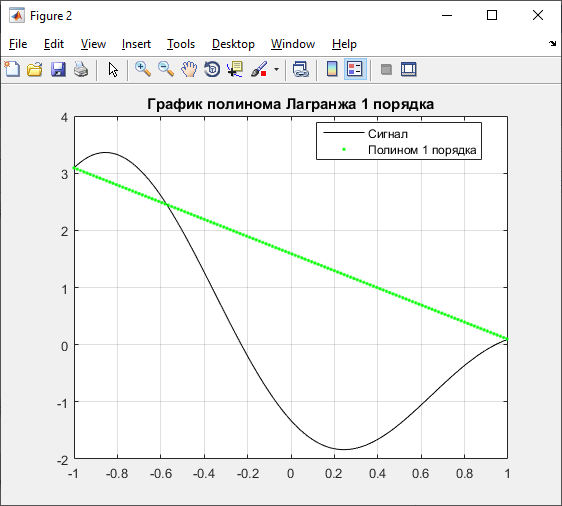

Полином Лагранжа 2 порядка:
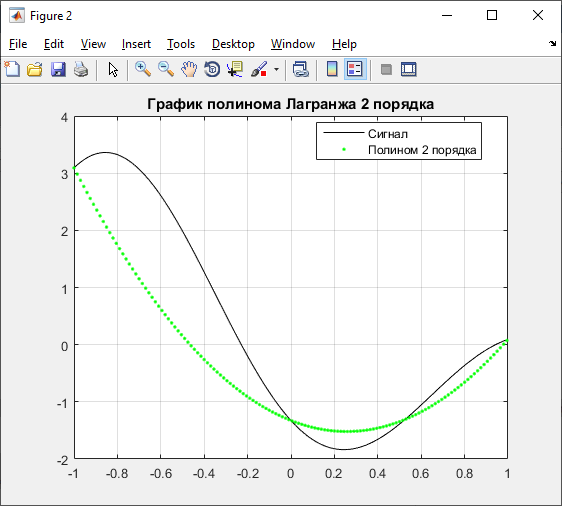

Полином Лагранжа 3 порядка:
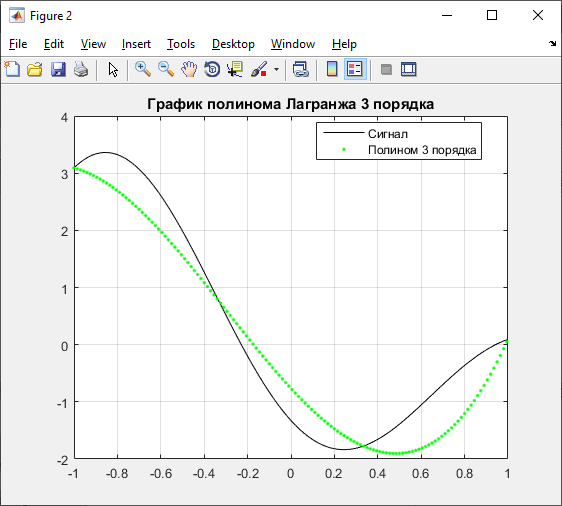

Коды программ
Полином Лагранжа 0 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=-1;%узловые точки
f0=3.0916;
p=f0;
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 0 порядка');
legend ('Сигнал','Полином 0 порядка','Location','Best');
ep0=xt-p;%эмпирическая погрешность
dx1=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
m1=max(abs(dx1));
q1=(t-t0);
es0=m1*max(abs(q1));
figure(3);
plot([-1 1], [es0 es0], 'k--');
hold on;
plot(t, ep0, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('0 порядок');
Полином Лагранжа 1 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=-1;%узловые точки
t1=1;
f0=3.0916;
f1=0.094;
p=(f0*(t-t1)/(t0-t1))+(f1*(t-t0)/(t1-t0));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 1 порядка');
legend ('Сигнал','Полином 1 порядка','Location','Best');
ep1=xt-p;%эмпирическая погрешность
dx2=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
m2=max(abs(dx2));
q2=(t-t0).*(t-t1);
es1=m2*max(abs(q2))/2;
figure(3);
plot([-1 1], [es1 es1], 'k--');
hold on;
plot(t, ep1, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('1 порядок');
Полином Лагранжа 2 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=-1;%узловые точки
t1=0;
t2=1;
f0=3.0916;
f1=-1.327;
f2=0.094;
p=(f0*(t-t1).*(t-t2))/((t0-t1).*(t0-t2))+(f1*(t-t0).*(t-t2))/((t1-t0).*(t1-t2))+(f2*(t-t0).*(t-t1))/((t2-t0).*(t2-t1));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 2 порядка');
legend ('Сигнал','Полином 2 порядка','Location','Best');
ep2=xt-p;%эмпирическая погрешность
dx3=-(pi^3)*(2*sin(pi*t)+1/2*sqrt(2)*cos(sqrt(2)*pi*(t+55)/2));%оценка сверху максимальной погрешности
m3=max(abs(dx3));
q3=(t-t0).*(t-t1).*(t-t2);
es2=m3*max(abs(q3))/(2*3);
figure(3);
plot([-1 1], [es2 es2], 'k--');
hold on;
plot(t, ep2, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('2 порядок');
Полином Лагранжа 3 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=-1;%узловые точки
t1=-1/3;
t2=1/3;
t3=1;
f0=3.0916;
f1=0.767;
f2=-1.7745;
f3=0.094;
p=(f0*(t-t1).*(t-t2).*(t-t3))/((t0-t1).*(t0-t2).*(t0-t3))+(f1*(t-t0).*(t-t2).*(t-t3))/((t1-t0).*(t1-t2).*(t1-t3))+(f2*(t-t0).*(t-t1).*(t-t3))/((t2-t0).*(t2-t1).*(t2-t3))+(f3*(t-t0).*(t-t1).*(t-t2))/((t3-t0).*(t3-t1).*(t3-t2));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 3 порядка');
legend ('Сигнал','Полином 3 порядка','Location','Best');
ep3=xt-p;%эмпирическая погрешность
dx4=pi^4/2*sin((sqrt(2)*pi*(t+55))/2)-pi^4*2*cos(pi*t);%оценка сверху максимальной погрешности
m4=max(abs(dx4));
q4=(t-t0).*(t-t1).*(t-t2).*(t-t3);
es3=m4*max(abs(q4))/(2*3*4);
figure(3);
plot([-1 1], [es3 es3], 'k--');
hold on;
plot(t, ep3, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('3 порядок');
Описание сигнала по Чебышеву
Полином 0 порядка:

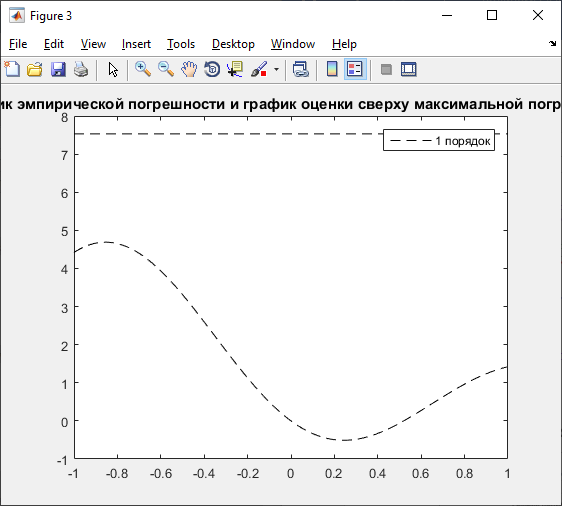
Полином 1 порядка:

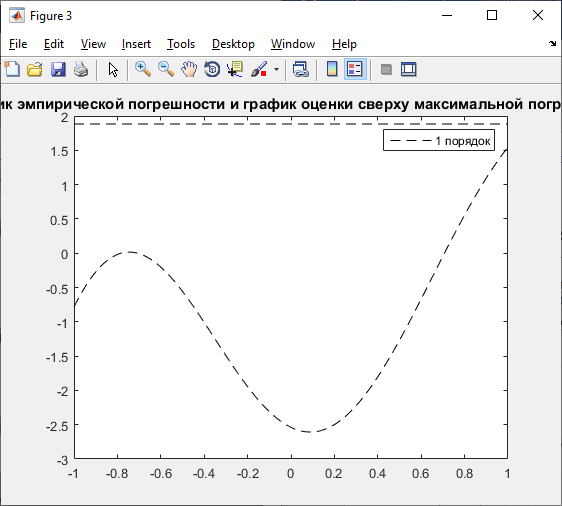
Полином 2 порядка:
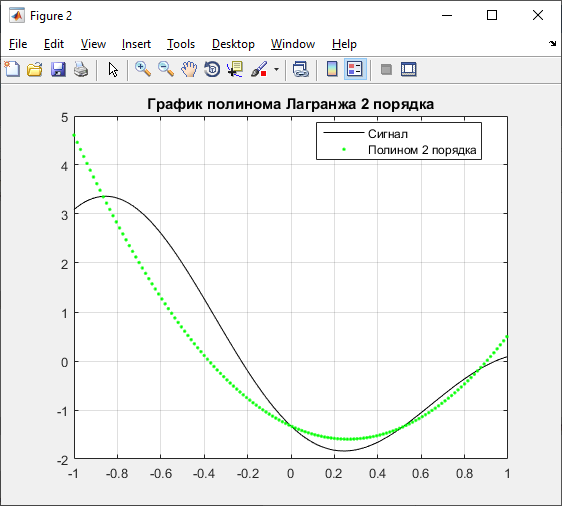

Полином 3 порядка:

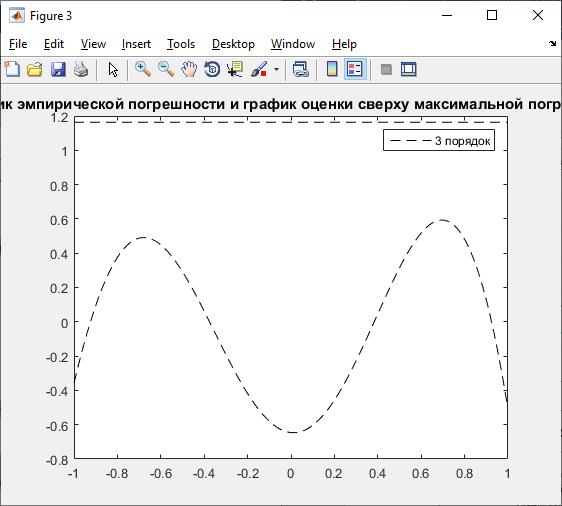
Узловые
точки:
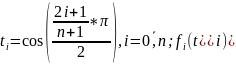
Порядок |
t0 |
t1 |
t2 |
t3 |
0 |
0 |
|
|
|
1 |
0.7071 |
-0.7071 |
|
|
2 |
0.8660 |
0 |
-0.8660 |
|
3 |
0.9239 |
0.3827 |
-0.3827 |
-0.9239 |
Порядок |
f0 |
f1 |
f2 |
f3 |
0 |
-1.3277 |
|
|
|
1 |
-0.6722 |
3.095 |
|
|
2 |
-0.1745 |
-1.3277 |
3.3605 |
|
3 |
-0.0376 |
-1.6921 |
1.1385 |
3.301 |
Из таблицы видно, что точки выбраны верно, т.к. соблюдается симметрия относительно нуля.
Реальная
погрешность:

Оценка
максимальной погрешности:
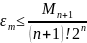
Из графиков видно, что значения реальной погрешности не превышают значения оценки максимальной погрешности, что свидетельствует о правильности вычислений.
Коды программ
Полином 0 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=0;%узловые точки, вычисленные по способы Чебышева
f0=-1.3277;
p=f0;
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 1 порядка');
legend ('Сигнал','Полином 1 порядка','Location','Best');
ep0=xt-p;%эмпирическая погрешность
dx1=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
m1=max(abs(dx1));
es0=m1/((1)*2^0);
figure(3);
plot([-1 1], [es0 es0], 'k--');
hold on;
plot(t, ep0, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('1 порядок');
Полином 1 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=0.7071;%узловые точки, вычисленные по способы Чебышева
t1=-0.7071;
f0=-0.6722;
f1=3.095;
p=(f0*(t-t1)/(t0-t1))+(f1*(t-t0)/(t1-t0));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 1 порядка');
legend ('Сигнал','Полином 1 порядка','Location','Best');
ep1=xt-p;%эмпирическая погрешность
dx2=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
m2=max(abs(dx2));
es1=m2/((2)*2^1);
figure(3);
plot([-1 1], [es1 es1], 'k--');
hold on;
plot(t, ep1, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('1 порядок');
Полином 2 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=0.866;%узловые точки, вычисленные по способы Чебышева
t1=0;
t2=-0.866;
f0=-0.1745;
f1=-1.3277;
f2=3.3605;
p=(f0*(t-t1).*(t-t2))/((t0-t1).*(t0-t2))+(f1*(t-t0).*(t-t2))/((t1-t0).*(t1-t2))+(f2*(t-t0).*(t-t1))/((t2-t0).*(t2-t1));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 2 порядка');
legend ('Сигнал','Полином 2 порядка','Location','Best');
ep2=xt-p;%эмпирическая погрешность
dx3=-(pi^3)*(2*sin(pi*t)+1/2*sqrt(2)*cos(sqrt(2)*pi*(t+55)/2));;%оценка сверху максимальной погрешности
m3=max(abs(dx3));
es2=m3/((2*3)*2^2);
figure(3);
plot([-1 1], [es2 es2], 'k--');
hold on;
plot(t, ep2, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('2 порядок');
Полином 3 порядка:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
figure(1);
plot(Tau,x,'k');
hold on;
grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
figure(2);
plot(t,xt,'k');
hold on;
grid on;
t0=0.9239;%узловые точки, вычисленные по способы Чебышева
t1=0.3827;
t2=-0.3827;
t3=-0.9239;
f0=-0.0376;
f1=-1.6921;
f2=1.1385;
f3=3.301;
p=(f0*(t-t1).*(t-t2).*(t-t3))/((t0-t1).*(t0-t2).*(t0-t3))+(f1*(t-t0).*(t-t2).*(t-t3))/((t1-t0).*(t1-t2).*(t1-t3))+(f2*(t-t0).*(t-t1).*(t-t3))/((t2-t0).*(t2-t1).*(t2-t3))+(f3*(t-t0).*(t-t1).*(t-t2))/((t3-t0).*(t3-t1).*(t3-t2));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 3 порядка');
legend ('Сигнал','Полином 3 порядка','Location','Best');
ep3=xt-p;%эмпирическая погрешность
dx4=pi^4/2*sin((sqrt(2)*pi*(t+55))/2)-pi^4*2*cos(pi*t);%оценка сверху максимальной погрешности
m4=max(abs(dx4));
es3=m4/((2*3*4)*2^3);
figure(3);
plot([-1 1], [es3 es3], 'k--');
hold on;
plot(t, ep3, 'k--');
title ('График эмпирической погрешности и график оценки сверху максимальной погрешности');
legend('3 порядок');
