
1.5 Описание сигнала по Лежандру
А) 0 порядок:









Рисунок 19 – Графики полинома и погрешностей 0 порядка
Б) 1 порядок:





Рисунок 20 – Графики полинома и погрешностей 1 порядка



Б) 2 порядок:





Рисунок 21 – Графики полинома и погрешностей 2 порядка



Б) 3 порядок:





Рисунок 22 – Графики полинома и погрешностей 3 порядка



Из графиков видно, что вычисления
сделаны верно, так как значения
 меньше максимальных значений эмпирических
погрешностей.
меньше максимальных значений эмпирических
погрешностей.
1.6 Описание сигнала по Уолшу



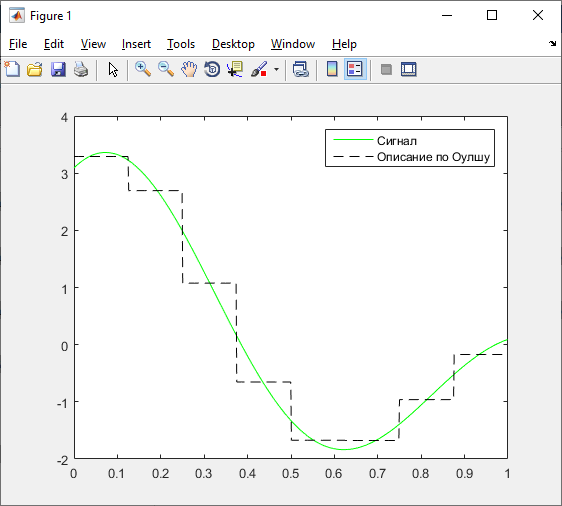
Рисунок 23 – Сигнал и описание сигнала по Уолшу


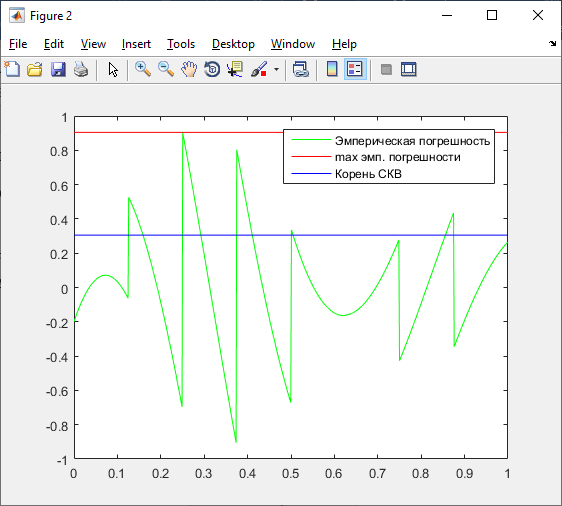
Рисунок 23 – График эмпирической, максимума эмпирической и СКВ погрешностей
1.6 Полиномы наилучшего приближения

Рисунок 24 – График полиномов наилучшего приближения 0 – 2 порядков
А) 0 порядок:


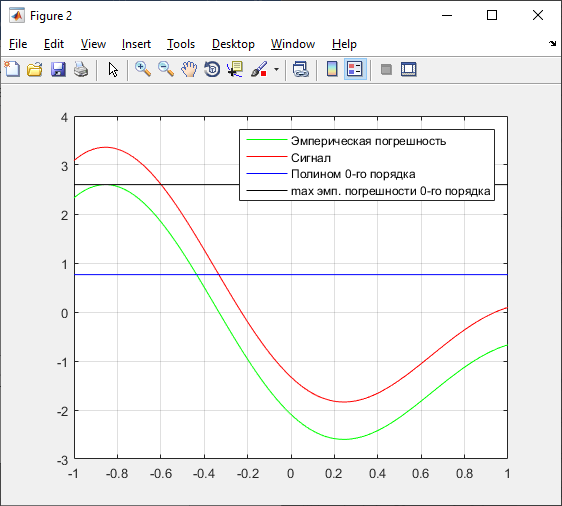
Рисунок 25 – График полинома наилучшего приближения 0 порядка
Б) 1 порядок:



Рисунок 26 – График полинома наилучшего приближения 1 порядка
В) 2 порядок:



Рисунок 27 – График полинома наилучшего приближения 2 порядка
Спектральное описание сигнала
Таблица 3 – Постоянные амплитуды
косинусов ( )
и синусов (
)
и синусов ( )
)
№ Гармоники |
a |
b |
№ Гармоники |
a |
b |
1 |
-1,5184 |
-1,9083 |
11 |
0,0020 |
-0,0871 |
2 |
-0,0688 |
0,5452 |
12 |
-0,0017 |
0,0798 |
3 |
0,0283 |
-0,3368 |
13 |
0,0014 |
-0,0736 |
4 |
-0,0155 |
0,2462 |
14 |
-0,0012 |
0,0683 |
5 |
-0,0098 |
-0,1947 |
15 |
0,0011 |
-0,0638 |
6 |
-0,0068 |
0,1613 |
16 |
-0,0009 |
0,0598 |
7 |
0,0050 |
-0,1377 |
17 |
-0,0008 |
-0,0562 |
8 |
-0,0038 |
0,1202 |
18 |
-0,0007 |
0,0531 |
9 |
0,0030 |
-0,1067 |
19 |
-0,0006 |
-0,0503 |
10 |
-0,0024 |
-0,0959 |
20 |
-0,0006 |
0,0478 |


Рисунок 28 – Амплитудный спектр сигнала.
Таблица 4 – Фаза
№ гармоники |
|
№ гармоники |
|
1 |
2,2429 |
11 |
1,5479 |
2 |
4,5869 |
12 |
4,6914 |
3 |
1,4869 |
13 |
1,5514 |
4 |
4,6494 |
14 |
4,6944 |
5 |
1,5204 |
15 |
1,5540 |
6 |
4,6703 |
16 |
4,6966 |
7 |
1,5348 |
17 |
1,5560 |
8 |
4,6809 |
18 |
4,6984 |
9 |
1,5428 |
19 |
1,5575 |
10 |
4,6872 |
20 |
4,6998 |
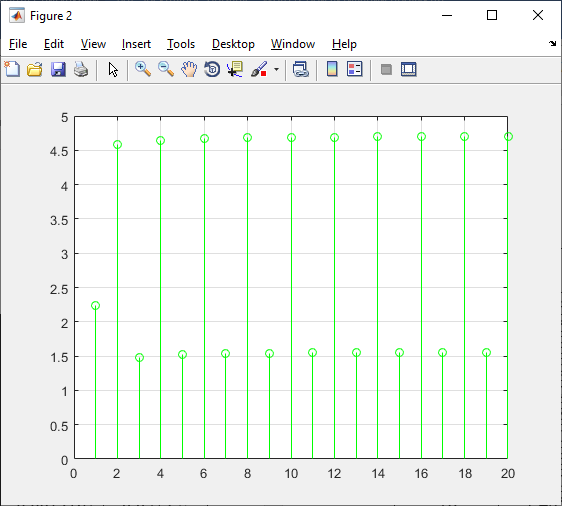
Рисунок 29 – Фазовый спектр сигнала.

Рисунок 30 – Восстановленный сигнал с помощью
спектрального описания.

Рисунок 31 – Погрешности описания.
Максимальная эмпирическая погрешность

СКВ

Вывод: в ходе выполнения курсовой работы были закреплены знания, полученные при изучении основных разделов курса «преобразование измерительных сигналов».
Исходный сигнал был масштабирован на интервале [-1, 1], были сделаны описания сигнала по Лагранжу, Чебышеву, Тейлору, Лежандру Уолшу и полиномами наилучшего приближения; также было построено спектральное описание сигнала. Были построены их графики.
Для всех описаний были найдены эмпирические погрешности и СКВ, были построены их графики. Там, где необходимо были приведены аналитические выражения полиномов, таблицы координат узловых точек, постоянных амплитуды косинусов ( ) и синусов ( ) и фазы.
Код программы:
Taun=27*pi;
deltaTau=0.015;
Tauv=28*pi;
Tau=Taun:deltaTau:Tauv;
x=2*cos(2*Tau)+2*sin(sqrt(2)*Tau);%исходный сигнал от Tau
%figure(1);
%plot(Tau,x,'k');
%hold on;
%grid on;
t=-1:deltaTau:1;
xt=2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi));%сигнал от t
%figure(2);
%plot(t,xt,'k');
%hold on;
%grid on;
%Описание сигнала по Лагранжу
%Полином Лагранжа 0 порядка
t00L=0;%узловые точки
f00L=-1.327;
p0L=f00L;
ep0L=xt-p0L;%эмпирическая погрешность
mep0L=max(abs(ep0L));
dx1L=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
m1L=max(abs(dx1L));
q1L=(t-t00L);
es0L=m1L*max(abs(q1L));
%Полином Лагранжа 1 порядка
t01L=-1;%узловые точки
t11L=1;
f01L=3.0916;
f11L=0.094;
p1L=(f01L*(t-t11L)/(t01L-t11L))+(f11L*(t-t01L)/(t11L-t01L));
ep1L=xt-p1L;%эмпирическая погрешность
mep1L=max(abs(ep1L));
dx2L=2*pi^2*cos(pi*t)-pi^2*sin(sqrt(2)*(pi*t/2+55/2*pi));%оценка сверху максимальной погрешности
m2L=max(abs(dx2L));
q2L=(t-t01L).*(t-t11L);
es1L=m2L*max(abs(q2L))/2;
%Полином Лагранжа 2 порядка
t02L=-1;%узловые точки
t12L=0;
t22L=1;
f02L=3.0916;
f12L=-1.327;
f22L=0.094;
p2L=(f02L*(t-t12L).*(t-t22L))/((t02L-t12L).*(t02L-t22L))+(f12L*(t-t02L).*(t-t22L))/((t12L-t02L).*(t12L-t22L))+(f22L*(t-t02L).*(t-t12L))/((t22L-t02L).*(t22L-t12L));
ep2L=xt-p2L;%эмпирическая погрешность
mep2L=max(abs(ep2L));
dx3L=-(pi^3)*(2*sin(pi*t)+1/2*sqrt(2)*cos(sqrt(2)*pi*(t+55)/2));%оценка сверху максимальной погрешности
m3L=max(abs(dx3L));
q3L=(t-t02L).*(t-t12L).*(t-t22L);
es2L=m3L*max(abs(q3L))/(2*3);
%Полином Лагранжа 3 порядка
t03L=-1;%узловые точки
t13L=-1/3;
t23L=1/3;
t33L=1;
f03L=3.0916;
f13L=0.767;
f23L=-1.7745;
f33L=0.094;
p3L=(f03L*(t-t13L).*(t-t23L).*(t-t33L))/((t03L-t13L).*(t03L-t23L).*(t03L-t33L))+(f13L*(t-t03L).*(t-t23L).*(t-t33L))/((t13L-t03L).*(t13L-t23L).*(t13L-t33L))+(f23L*(t-t03L).*(t-t13L).*(t-t33L))/((t23L-t03L).*(t23L-t13L).*(t23L-t33L))+(f33L*(t-t03L).*(t-t13L).*(t-t23L))/((t33L-t03L).*(t33L-t13L).*(t33L-t23L));
ep3L=xt-p3L;%эмпирическая погрешность
mep3L=max(abs(ep3L));
dx4L=pi^4/2*sin((sqrt(2)*pi*(t+55))/2)-pi^4*2*cos(pi*t);%оценка сверху максимальной погрешности
m4L=max(abs(dx4L));
q4L=(t-t03L).*(t-t13L).*(t-t23L).*(t-t33L);
es3L=m4L*max(abs(q4L))/(2*3*4);
%{
%Графики
figure(3);%график полинома 0 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p0L,'g.');
hold on;
title ('График полинома Лагранжа 0 порядка');
legend ('Сигнал','Полином 0 порядка','Location','Best');
figure(4);%график полинома 1 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p1L,'g.');
hold on;
title ('График полинома Лагранжа 1 порядка');
legend ('Сигнал','Полином 1 порядка','Location','Best');
figure(5);%график погрешностей 0 и 1 порядка
plot([-1 1],[es0L es0L],'g--');
hold on;
grid on;
plot(t,ep0L,'g');
hold on;
plot([-1 1],[mep0L mep0L],'-.g');
hold on;
plot([-1 1],[es1L es1L],'b--');
hold on;
plot(t,ep1L,'b');
hold on;
plot([-1 1],[mep1L mep1L],'-.b');
hold on;
title ('График погрешностей полиномов Лагранжа 0 и 1 порядка');
legend ('Оценка макс. погр. 0 порядок','Эмп. погр. 0 порядок','Макс. эмп. погр. 0 порядок','Оценка макс. погр. 1 порядок','Эмп. погр. 1 порядок','Макс. эмп. погр. 1 порядок','Location','Best');
figure(6);%график полинома 2 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p2L,'g.');
hold on;
title ('График полинома Лагранжа 2 порядка');
legend ('Сигнал','Полином 2 порядка','Location','Best');
figure(7);%график полинома 3 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p3L,'g.');
hold on;
title ('График полинома Лагранжа 3 порядка');
legend ('Сигнал','Полином 3 порядка','Location','Best');
figure(8);%график погрешностей 2 и 3 порядка
plot([-1 1],[es2L es2L],'g--');
hold on;
grid on;
plot(t,ep2L,'g');
hold on;
plot([-1 1],[mep2L mep2L],'-.g');
hold on;
plot([-1 1],[es3L es3L],'b--');
hold on;
plot(t,ep3L,'b');
hold on;
plot([-1 1],[mep3L mep3L],'-.b');
hold on;
title ('График погрешностей полиномов Лагранжа 2 и 3 порядка');
legend ('Оценка макс. погр. 2 порядок','Эмп. погр. 2 порядок','Макс. эмп. погр. 2 порядок','Оценка макс. погр. 3 порядок','Эмп. погр. 3 порядок','Макс. эмп. погр. 3 порядок','Location','Best');
%}
%Описание сигнала по Чебышеву
%Полином Лагранжа по точкам Чебышева 0 порядка
t00CH=0;%узловые точки, вычисленные по способы Чебышева
f00CH=-1.3277;
p0CH=f00CH;
ep0CH=xt-p0CH;%эмпирическая погрешность
mep0CH=max(abs(ep0CH));
dx1CH=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
m1CH=max(abs(dx1CH));
es0CH=m1CH/((1)*2^0);
%Полином Лагранжа по точкам Чебышева 1 порядка
t01CH=0.7071;%узловые точки, вычисленные по способы Чебышева
t11CH=-0.7071;
f01CH=-0.6722;
f11CH=3.095;
p1CH=(f01CH*(t-t11CH)/(t01CH-t11CH))+(f11CH*(t-t01CH)/(t11CH-t01CH));
ep1CH=xt-p1CH;%эмпирическая погрешность
mep1CH=max(abs(ep1CH));
dx2CH=2*pi^2*cos(pi*t)-pi^2*sin(sqrt(2)*(pi*t/2+55/2*pi));%оценка сверху максимальной погрешности
m2CH=max(abs(dx2CH));
es1CH=m2CH/((2)*2^1);
%Полином Лагранжа по точкам Чебышева 2 порядка
t02CH=0.866;%узловые точки, вычисленные по способы Чебышева
t12CH=0;
t22CH=-0.866;
f02CH=-0.1745;
f12CH=-1.3277;
f22CH=3.3605;
p2CH=(f02CH*(t-t12CH).*(t-t22CH))/((t02CH-t12CH).*(t02CH-t22CH))+(f12CH*(t-t02CH).*(t-t22CH))/((t12CH-t02CH).*(t12CH-t22CH))+(f22CH*(t-t02CH).*(t-t12CH))/((t22CH-t02CH).*(t22CH-t12CH));
ep2CH=xt-p2CH;%эмпирическая погрешность
mep2CH=max(abs(ep2CH));
dx3CH=-(pi^3)*(2*sin(pi*t)+1/2*sqrt(2)*cos(sqrt(2)*pi*(t+55)/2));%оценка сверху максимальной погрешности
m3CH=max(abs(dx3CH));
es2CH=m3CH/((2*3)*2^2);
%Полином Лагранжа по точкам Чебышева 3 порядка
t03CH=0.9239;%узловые точки, вычисленные по способы Чебышева
t13CH=0.3827;
t23CH=-0.3827;
t33CH=-0.9239;
f03CH=-0.0376;
f13CH=-1.6921;
f23CH=1.1385;
f33CH=3.301;
p3CH=(f03CH*(t-t13CH).*(t-t23CH).*(t-t33CH))/((t03CH-t13CH).*(t03CH-t23CH).*(t03CH-t33CH))+(f13CH*(t-t03CH).*(t-t23CH).*(t-t33CH))/((t13CH-t03CH).*(t13CH-t23CH).*(t13CH-t33CH))+(f23CH*(t-t03CH).*(t-t13CH).*(t-t33CH))/((t23CH-t03CH).*(t23CH-t13CH).*(t23CH-t33CH))+(f33CH*(t-t03CH).*(t-t13CH).*(t-t23CH))/((t33CH-t03CH).*(t33CH-t13CH).*(t33CH-t23CH));
ep3CH=xt-p3CH;%эмпирическая погрешность
mep3CH=max(abs(ep3CH));
dx4CH=pi^4/2*sin((sqrt(2)*pi*(t+55))/2)-pi^4*2*cos(pi*t);%оценка сверху максимальной погрешности
m4CH=max(abs(dx4CH));
es3CH=m4CH/((2*3*4)*2^3);
%{
%Графики
figure(9);%график полинома Лагранжа по точкам Чебышева 0 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p0CH,'g.');
hold on;
title ('График полинома Лагранжа по точкам Чебышева 0 порядка');
legend ('Сигнал','Полином 0 порядка','Location','Best');
figure(10);%график полинома Лагранжа по точкам Чебышева 1 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p1CH,'g.');
hold on;
title ('График полинома Лагранжа по точкам Чебышева 1 порядка');
legend ('Сигнал','Полином 1 порядка','Location','Best');
figure(11);%график погрешностей 0 и 1 порядка
plot([-1 1],[es0CH es0CH],'g--');
hold on;
grid on;
plot(t,ep0CH,'g');
hold on;
plot([-1 1],[mep0CH mep0CH],'-.g');
hold on;
plot([-1 1],[es1CH es1CH],'b--');
hold on;
plot(t,ep1CH,'b');
hold on;
plot([-1 1],[mep1CH mep1CH],'-.b');
hold on;
title ('График погрешностей полиномов Лагранжа по точкам Чебышева 0 и 1 порядка');
legend ('Оценка макс. погр. 0 порядок','Эмп. погр. 0 порядок','Макс. эмп. погр. 0 порядок','Оценка макс. погр. 1 порядок','Эмп. погр. 1 порядок','Макс. эмп. погр. 1 порядок','Location','Best');
figure(12);%график полинома Лагранжа по точкам Чебышева 2 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p2CH,'g.');
hold on;
title ('График полинома Лагранжа по точкам Чебышева 2 порядка');
legend ('Сигнал','Полином 2 порядка','Location','Best');
figure(13);%график полинома Лагранжа по точкам Чебышева 3 порядка
plot(t,xt,'k');
hold on;
grid on;
plot(t,p3CH,'g.');
hold on;
title ('График полинома Лагранжа по точкам Чебышева 3 порядка');
legend ('Сигнал','Полином 3 порядка','Location','Best');
figure(14);%график погрешностей 2 и 3 порядка
plot([-1 1],[es2CH es2CH],'g--');
hold on;
grid on;
plot(t,ep2CH,'g');
hold on;
plot([-1 1],[mep2CH mep2CH],'-.g');
hold on;
plot([-1 1],[es3CH es3CH],'b--');
hold on;
plot(t,ep3CH,'b');
hold on;
plot([-1 1],[mep3CH mep3CH],'-.b');
hold on;
title ('График погрешностей полиномов Лагранжа по точкам Чебышева 2 и 3 порядка');
legend ('Оценка макс. погр. 2 порядок','Эмп. погр. 2 порядок','Макс. эмп. погр. 2 порядок','Оценка макс. погр. 3 порядок','Эмп. погр. 3 порядок','Макс. эмп. погр. 3 порядок','Location','Best');
%}
%Описание сигнала по Тейлору
t0T=0;
f0T=2*cos(pi*0+55*pi)+2*sin(sqrt(2)*(pi*0/2+27.5*pi));
dx0T=f0T;%производные
dx1T=2*pi*sin(pi*t0T)+sqrt(2)*pi*cos(sqrt(2)*(pi*t0T/2+55*pi/2));
dx2T=2*pi^2*cos(pi*t0T)-pi^2*sin(sqrt(2)*(pi*t0T/2+55/2*pi));
dx3T=-(pi^3)*(2*sin(pi*t0T)+1/2*sqrt(2)*cos(sqrt(2)*pi*(t0T+55)/2));
p0T=dx0T;%полиномы Тейлора
p1T=dx0T+dx1T*t;
p2T=dx0T+dx1T*t+1/2*dx2T*t.^2;
p3T=dx0T+dx1T*t+1/2*dx2T*t.^2+1/6*dx3T*t.^3;
ep0T=xt-p0T;%эмпирическая погрешность
ep1T=xt-p1T;
ep2T=xt-p2T;
ep3T=xt-p3T;
mep0T=max(abs(ep0T));
mep1T=max(abs(ep1T));
mep2T=max(abs(ep2T));
mep3T=max(abs(ep3T));
dx1tT=2*pi*sin(pi*t)+sqrt(2)*pi*cos(sqrt(2)*(pi*t/2+55*pi/2));%оценка сверху максимальной погрешности
dx2tT=2*pi^2*cos(pi*t)-pi^2*sin(sqrt(2)*(pi*t/2+55/2*pi));
dx3tT=-(pi^3)*(2*sin(pi*t)+1/2*sqrt(2)*cos(sqrt(2)*pi*(t+55)/2));
dx4tT=pi^4/2*sin((sqrt(2)*pi*(t+55))/2)-pi^4*2*cos(pi*t);
m1T=max(abs(dx1tT));
es0T=m1T/(1);
m2T=max(abs(dx2tT));
es1T=m2T/(2);
m3T=max(abs(dx3tT));
es2T=m3T/(2*3);
m4T=max(abs(dx4tT));
es3T=m4T/(2*3*4);
%{
%Графики
figure(15);
plot(t,xt,'k');
hold on;
grid on;
plot(t,p0T,'g.');
hold on;
title ('График полинома Тейлора 0 порядка');
legend('Сигнал','П. Тейлора 0 порядка','Location','Best');
figure(16);
plot(t,xt,'k');
hold on;
grid on;
plot(t,p1T,'g.');
hold on;
title ('График полинома Тейлора 1 порядка');
legend('Сигнал','П. Тейлора 1 порядка','Location','Best');
figure(17);
plot(t,xt,'k');
hold on;
grid on;
plot(t,p2T,'g.');
hold on;
title ('График полинома Тейлора 2 порядка');
legend('Сигнал','П. Тейлора 2 порядка','Location','Best');
figure(18);
plot(t,xt,'k');
hold on;
grid on;
plot(t,p3T,'g.');
hold on;
title ('График полинома Тейлора 3 порядка');
legend('Сигнал','П. Тейлора 3 порядка','Location','Best');
figure(19);
plot([-1 1],[es0T es0T],'g--');
hold on;
grid on;
plot(t,ep0T,'g');
hold on;
plot([-1 1],[mep0T mep0T],'-.g');
hold on;
plot([-1 1],[es1T es1T],'b--');
hold on;
plot(t,ep1T,'b');
hold on;
plot([-1 1],[mep1T mep1T],'-.b');
hold on;
title ('График погрешностей полиномов Тейлора 0 и 1 порядка');
legend ('Оценка макс. погр. 0 порядок','Эмп. погр. 0 порядок','Макс. эмп. погр. 0 порядок','Оценка макс. погр. 1 порядок','Эмп. погр. 1 порядок','Макс. эмп. погр. 1 порядок','Location','Best');
figure(20);
plot([-1 1],[es2T es2T],'g--');
hold on;
grid on;
plot(t,ep2T,'g');
hold on;
plot([-1 1],[mep2T mep2T],'-.g');
hold on;
plot([-1 1],[es3T es3T],'b--');
hold on;
plot(t,ep3T,'b');
hold on;
plot([-1 1],[mep3T mep3T],'-.b');
hold on;
title ('График погрешностей полиномов Тейлора 2 и 3 порядка');
legend ('Оценка макс. погр. 2 порядок','Эмп. погр. 2 порядок','Макс. эмп. погр. 2 порядок','Оценка макс. погр. 3 порядок','Эмп. погр. 3 порядок','Макс. эмп. погр. 3 порядок','Location','Best');
%}
%Описание сигнала по Лежандру
p0Le=1;%полиномы Лежандра
p1Le=t;
p2Le=1/2*(3*t.*t-1);
p3Le=1/2*(5*t.*t.*t-3*t);
fun0Le=@(t) ((2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi)))*1);%Функции для интегрирования
fun1Le=@(t) ((2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi))).*t);
fun2Le=@(t) ((2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi))).*(1/2*(3*t.*t-1)));
fun3Le=@(t) ((2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi))).*(1/2*(5*t.*t.*t-3*t)));
c0Le=1/2*integral(fun0Le,-1,1);%Постоянные коэффициенты
c1Le=3/2*integral(fun1Le,-1,1);
c2Le=5/2*integral(fun2Le,-1,1);
c3Le=7/2*integral(fun3Le,-1,1);
f0Le=p0Le*c0Le;%Описание сигнала по Лежандру
f1Le=p0Le*c0Le+p1Le*c1Le;
f2Le=p0Le*c0Le+p1Le*c1Le+p2Le*c2Le;
f3Le=p0Le*c0Le+p1Le*c1Le+p2Le*c2Le+p3Le*c3Le;
ep0Le=xt-f0Le;%эмпирическая погрешность
ep1Le=xt-f1Le;
ep2Le=xt-f2Le;
ep3Le=xt-f3Le;
mep0Le=max(abs(ep0Le));
mep1Le=max(abs(ep1Le));
mep2Le=max(abs(ep2Le));
mep3Le=max(abs(ep3Le));
funLe=@(t) ((2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi))).*(2*cos(pi*t+55*pi)+2*sin(sqrt(2)*(pi*t/2+27.5*pi))));%ЕСКВ
iLe=integral(funLe,-1,1);
epsq0Le=1/2*(iLe-2*c0Le.*c0Le);
skv0Le=sqrt(epsq0Le);
epsq1Le=1/2*(iLe-(2/3*c1Le.*c1Le+2*c0Le.*c0Le));
skv1Le=sqrt(epsq1Le);
epsq2Le=1/2*(iLe-(2/5*c2Le.*c2Le+2/3*c1Le.*c1Le+2*c0Le.*c0Le));
skv2Le=sqrt(epsq2Le);
epsq3Le=1/2*(iLe-(2/7*c3Le.*c3Le+2/5*c2Le.*c2Le+2/3*c1Le.*c1Le+2*c0Le.*c0Le));
skv3Le=sqrt(epsq3Le);
%{
%Графики
figure(21);
plot(t,xt,'k');
hold on;
grid on;
plot([-1 1],[f0Le f0Le],'g');
hold on;
title ('График полинома Лежандра 0');
legend('Сигнал','П. Лежандра 0 порядка','Location','Best');
figure(22);
plot(t,xt,'k');
hold on;
grid on;
plot(t,f1Le,'g');
hold on;
title ('График полинома Лежандра 1');
legend('Сигнал','П. Лежандра 1 порядка','Location','Best');
figure(23);
plot(t,xt,'k');
hold on;
grid on;
plot(t,f2Le,'g');
hold on;
title ('График полинома Лежандра 2');
legend('Сигнал','П. Лежандра 2 порядка','Location','Best');
figure(24);
plot(t,xt,'k');
hold on;
grid on;
plot(t,f3Le,'g');
hold on;
title ('График полинома Лежандра 3');
legend('Сигнал','П. Лежандра 3 порядка','Location','Best');
figure(25);
plot(t,ep0Le,'g');
hold on;
grid on;
plot([-1 1],[mep0Le mep0Le],'-.g');
hold on;
plot([-1 1],[skv0Le skv0Le],'b');
hold on;
title ('График погрешностей полинома Лежандра 0 порядка');
legend ('Эмп. погр. 0 порядок','Макс. эмп. погр. 0 порядок','СКВ 0 порядок','Location','Best');
figure(26);
plot(t,ep1Le,'g');
hold on;
grid on;
plot([-1 1],[mep1Le mep1Le],'-.g');
hold on;
plot([-1 1],[skv1Le skv1Le],'b');
hold on;
title ('График погрешностей полинома Лежандра 1 порядка');
legend ('Эмп. погр. 1 порядок','Макс. эмп. погр. 1 порядок','СКВ 1 порядок','Location','Best');
figure(27);
plot(t,ep2Le,'g');
hold on;
grid on;
plot([-1 1],[mep2Le mep2Le],'-.g');
hold on;
plot([-1 1],[skv2Le skv2Le],'b');
hold on;
title ('График погрешностей полинома Лежандра 2 порядка');
legend ('Эмп. погр. 2 порядок','Макс. эмп. погр. 2 порядок','СКВ 2 порядок','Location','Best');
figure(28);
plot(t,ep3Le,'g');
hold on;
grid on;
plot([-1 1],[mep3Le mep3Le],'-.g');
hold on;
plot([-1 1],[skv3Le skv3Le],'b');
hold on;
title ('График погрешностей полинома Лежандра 3 порядка');
legend ('Эмп. погр. 3 порядок','Макс. эмп. погр. 3 порядок','СКВ 3 порядок','Location','Best');
%}
clear();
%Описание сигнала по Уолшу
Tdown=27*pi; %Нижняя граница ИО
Tup=28*pi; %Верхняя граница ИО
dt=0.0015;
%Масштабирование
tau = Tdown:dt:Tup;
tn=0.00001:dt:1;
T0 = (tn ) * (Tup - Tdown) + Tdown;
T0_alt = 2 * (tau - Tdown) / (Tup - Tdown) - 1;
X = (2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)));
%Описание
r1=(sign(sin(2*pi*tn)));
r2=(sign(sin(4*pi*tn)));
r3=(sign(sin(8*pi*tn)));
walt0=1;
walt1=r1;
walt2=r1.*r2;
walt3=r2;
walt4=r2.*r3;
walt5=r1.*r2.*r3;
walt6=r1.*r3;
walt7=r3;
%Коэфы обэмы
C0fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown))))*walt0);
C0 =integral(C0fun,0,1);
C1fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(2*pi*tn))));
C1 =integral(C1fun,0,1);
C2fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(2*pi*tn))).*(sign(sin(4*pi*tn))));
C2 =integral(C2fun,0,1);
C3fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(4*pi*tn))));
C3 =integral(C3fun,0,1);
C4fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(4*pi*tn))).*(sign(sin(8*pi*tn))));
C4 =integral(C4fun,0,1);
C5fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(2*pi*tn))).*(sign(sin(4*pi*tn))).*(sign(sin(8*pi*tn))));
C5 =integral(C5fun,0,1);
C6fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(2*pi*tn))).*(sign(sin(8*pi*tn))));
C6 =integral(C6fun,0,1);
C7fun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).*(sign(sin(8*pi*tn))));
C7 =integral(C7fun,0,1);
F=(C0*walt0+C1*walt1+C2*walt2+C3*walt3+C4*walt4+C5*walt5+C6*walt6+C7*walt7);
%Погрешности
e=X-F;
g=max(abs(e));
sumC=C0*C0+C1*C1+C2*C2+C3*C3+C4*C4+C5*C5+C6*C6+C7*C7;
Ffun=@(tn) (((2 * cos (2*((tn ) * (Tup - Tdown) + Tdown)) + 2 * sin(sqrt(2)*((tn ) * (Tup - Tdown) + Tdown)))).^2);
Fail=integral(Ffun,0,1);
Ekv=Fail-sumC;
sqrtEkv=sqrt(Ekv);
figure(1);
plot(tn, X, 'g');
hold on;
plot(tn, F, '--k');
legend('Сигнал','Описание по Оулшу');
hold on;
figure(2);
plot(tn, e, 'g');
hold on;
plot([0 1], [g g], 'r');
hold on;
plot([0 1], [sqrtEkv sqrtEkv], 'b');
hold on;
legend('Эмперическая погрешность','max эмп. погрешности','Корень СКВ');
hold on;
clear();
%Полином наилучшего приблежения
Tdown=27*pi; %Нижняя граница ИО
Tup=28*pi; %Верхняя граница ИО
dt=0.0015;
%Масштабирование
tau = Tdown:dt:Tup;
T0 = 2 * (tau - Tdown) / (Tup - Tdown) - 1;
T0kv=(2 * (tau - Tdown) / (Tup - Tdown) - 1).^2;
X = 2 * cos (2 * ((T0+ 1) * (pi) / 2 + Tdown)) + 2 * sin(sqrt(2) * ((T0 + 1) * (pi) / 2 + Tdown));
XT0=X.*(2 * (tau - Tdown) / (Tup - Tdown) - 1);
P0 = (max(X)-abs(min(X)))/2;
coef=polyfit(T0,X,2);
Xpol=7.195*T0.*T0+1.6552*T0-2.9516;
Y=1.0391119*T0-0.3235143;
%Построение n=0 n=1 n=2
X1=2*cos(2*T0)+2*sin(T0*sqrt(2));
figure(1);
plot(T0, X, 'r');
hold on;
plot([-1 1], [P0 P0], 'g');
hold on;
plot(T0, Y, 'b');
hold on;
plot(T0, Xpol, 'k');
hold on;
legend('Сигнал','Полином 0-го порядка','Полином 1-го порядка','Полином 2-го порядка');
%Эмперическая
e0=X-P0;
e1=X-Y;
e2=X-Xpol;
g1=max(abs(e2));
g2=max(abs(e1));
g3=max(abs(e0));
%Графики погрешностей
figure(2);
plot(T0,e0,'g');
hold on;
plot(T0, X, 'r');
hold on;
plot([-1 1], [P0 P0], 'b');
hold on;
plot([-1 1], [g3 g3], 'k');
hold on;
legend('Эмперическая погрешность','Сигнал','Полином 0-го порядка','max эмп. погрешности 0-го порядка');
grid on;
hold on;
%
figure(3);
plot(T0,e1,'g');
hold on;
plot(T0, X, 'r');
hold on;
plot(T0, Y, 'b');
hold on;
plot([-1 1], [g2 g2], 'k');
hold on;
legend('Эмперическая погрешность','Сигнал','Полином 1-го порядка','max эмп. погрешности 1-го порядка');
grid on;
hold on;
%
figure(4);
plot(T0,e2,'g');
hold on;
plot(T0, X, 'r');
hold on;
plot(T0, Xpol, 'b');
hold on;
plot([-1 1], [g1 g1], 'k');
hold on;
legend('Эмперическая погрешность','Сигнал','Полином 2-го порядка','max эмп. погрешности 2-го порядка');
grid on;
hold on;
%ГрафоАнал Метод
em=max(X)-max(Y);
clear();
Tdown= 27*pi;
Tup= 28 * pi;
n=20;
dt=0.0005;
tau = Tdown:dt:Tup;
T0 = 2 * (tau - Tdown) / (Tup - Tdown) - 1;
X = 2 * cos (2 * ((T0+ 1) * (pi) / 2 + Tdown)) + 2 * sin(sqrt(2) * ((T0 + 1) * (pi) / 2 + Tdown));
w0 = 2 * pi / (1 -(-1));
T=1-(-1);
F=@(T0)(2 * cos (2 * ((T0+ 1) * (pi) / 2 + Tdown)) + 2 * sin(sqrt(2) * ((T0 + 1) * (pi) / 2 + Tdown)));
a0=(1/T) * integral(F,-1,1);
aosqrt=sqrt(a0^2);
b0=0;
q0=-atan(b0/a0);
for k=1:1:n
fcos=@(T0) ((2 * cos (2 * ((T0+ 1) * (pi) / 2 + Tdown)) + 2 * sin(sqrt(2) * ((T0 + 1) * (pi) / 2 + Tdown))).*(cos((k)*w0*T0)));
fsin=@(T0) ((2 * cos (2 * ((T0+ 1) * (pi) / 2 + Tdown)) + 2 * sin(sqrt(2) * ((T0 + 1) * (pi) / 2 + Tdown))).*(sin((k)*w0*T0)));
a(k)=(2/T)*(integral(fcos,-1,1));
b(k)=(2/T)*(integral(fsin,-1,1));
end
Fk=a0;
for k=1:1:n
A(k)=sqrt((b(k)^2)+(a(k)^2));
if (a(k)>=0)
q(k)=(-atan(b(k)/a(k)));
else
q(k)=(-atan(b(k)/(a(k)))+pi);
end
if (q(k)>(2*pi))
q(k)=q(k)-2*pi;
end
Fk=Fk+A(k) * cos(k*w0*T0+q(k));
end
F1=@(T0)((2 * cos (2 * ((T0 + 1) * (pi) / 2 + Tdown)) + 2 * sin(sqrt(2) * ((T0 + 1) * (pi) / 2 + Tdown))).^2);
F1s=(1/T) * integral(F1,-1,1);
a0s=a0^2;
for i = 1: 1: n
an = A(i);
a0s = a0s + (an^2) / 2;
end
Escv=sqrt(1-a0s/F1s)*100;
figure(1);
stem(0, a0,'g');
hold on;
stem(1: 1: n, A, 'g');
hold on;
grid on;
figure(2);
stem(1: 1: n, q,'g');
hold on;
grid on;
emp=max(abs(X - Fk));
figure(3);
plot(T0, Fk,'r');
hold on;
grid on;
hold on;
plot(T0, X, 'g');
hold on;
legend('Восстановленный сигнал','Сигнал');
hold on;
figure(4)
plot([-1 1],[emp emp],'r')
hold on;
grid on;
plot([-1 1], [Escv Escv],'g');
hold on;
plot(T0, X - Fk, 'b');
legend('Максимум эмпирической погрешности','СКВ','Эмпирическая погрешность')

