МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИИСТ
КУРСОВАЯ РАБОТА
по дисциплине «Преобразование измерительных сигналов»
Тема: Временное описание сигналов
Вариант № 27
Студент гр. 9587 |
|
Медведев Г.Н. |
Преподаватель |
|
Романцова Н.В. |
Санкт-Петербург
2022
Временное описание сигнала
1.1 Масштабирование сигнала
Исходный сигнал:
Описание сигналов удобнее вести не в
реальном времени
,
а в нормированной безразмерной переменной
t интервале [-1, 1], для этого
масштабирования необходимо произвести
линейное преобразование аргумента.
Переменная t и переменная связаны зависимостью:
где
и
– постоянные коэффициенты, определяемые
из условия
Отсюда следует, что
Нормированный сигнал:
Рисунок 1 – Графики исходного и нормированного сигналов
1.2 Описание сигнала по Лагранжу
Описание сигнала
по Лагранжу осуществляется с помощью
интерполяционного полинома Лагранжа,
который имеет вид:
где n – порядок описывающего
полинома,
– порядковые номера узловых точек
(узлов интерполяции),
– координаты узловых точек.
Аналитическое выражение для полиномов Лагранжа представляется в виде:
где
– постоянные коэффициенты.
Полиномы:
А) 0 порядок:
Рисунок 2 – График полинома Лагранжа 0 порядка
Б) 1 порядок:
Рисунок 2 – График полинома Лагранжа 1 порядка
В) 2 порядок:
Рисунок 3 – График полинома Лагранжа 2 порядка
Г) 3 порядок:
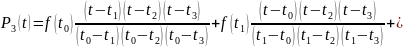
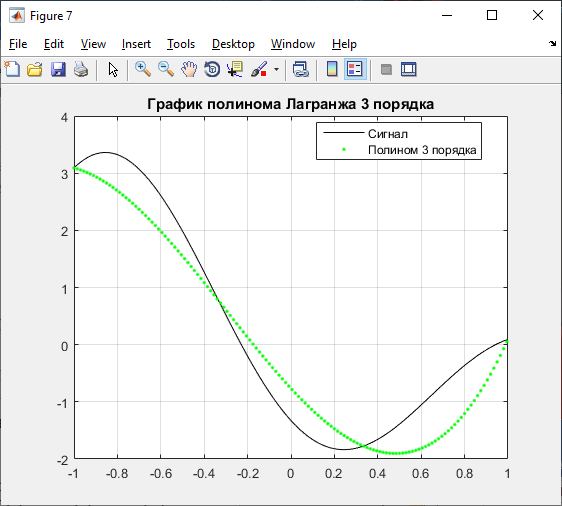
Рисунок 4 – График полинома Лагранжа 3 порядка
Таблица 1 – Координаты узловых точек
Порядок |
t0 |
t1 |
t2 |
t3 |
0 |
0 |
|
|
|
1 |
-1 |
1 |
|
|
2 |
-1 |
0 |
1 |
|
3 |
-1 |
-1/3 |
1/3 |
1 |
Порядок |
f0 |
f1 |
f2 |
f3 |
0 |
-1.3277 |
|
|
|
1 |
3.0916 |
0.094 |
|
|
2 |
3.0916 |
-1.327 |
0.094 |
|
3 |
3.0916 |
0.767 |
-1.7745 |
0.094 |
Эмпирическая погрешность, найденная из графиков для i-го полинома:
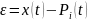
Оценка максимальной погрешности для i-го полинома:
где
– модуль-максимум (
)-й
производной сигнала на рассматриваемом
интервале.
Рисунок 5 – Графики погрешностей полиномов 0 и 1 порядков
Рисунок 6 – Графики погрешностей полиномов 2 и 3 порядков
Из графиков видно, что значения эмпирической погрешности не превышают значения оценки максимальной погрешности, что свидетельствует о правильности вычислений.