1.5 Описание сигнала по Лежандру
Полиномы Лежандра представляют собой
систему функций, ортогональных на
интервале
.
Общее выражение для полиномов Лежандра:
А) 0 порядок:
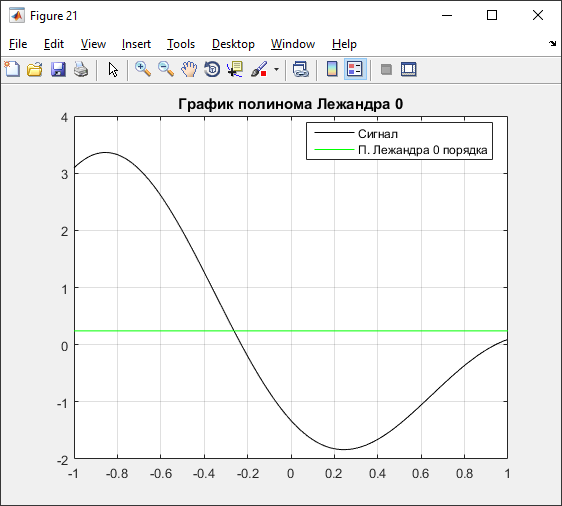
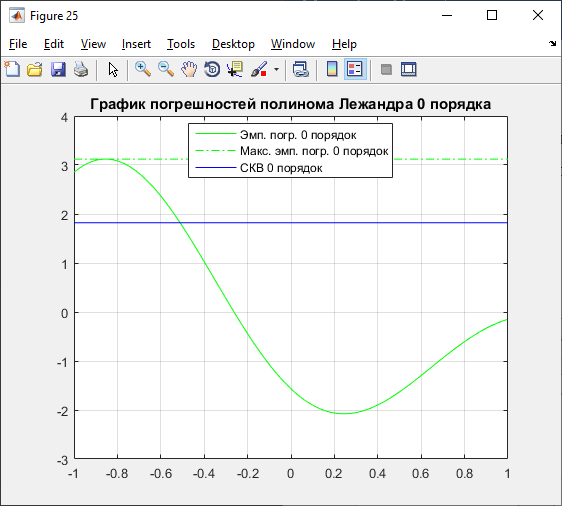
Рисунок 19 – Графики полинома и погрешностей 0 порядка
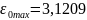
Б) 1 порядок:
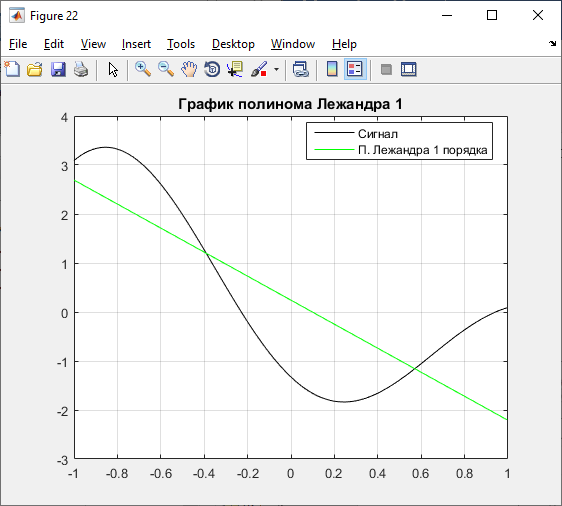
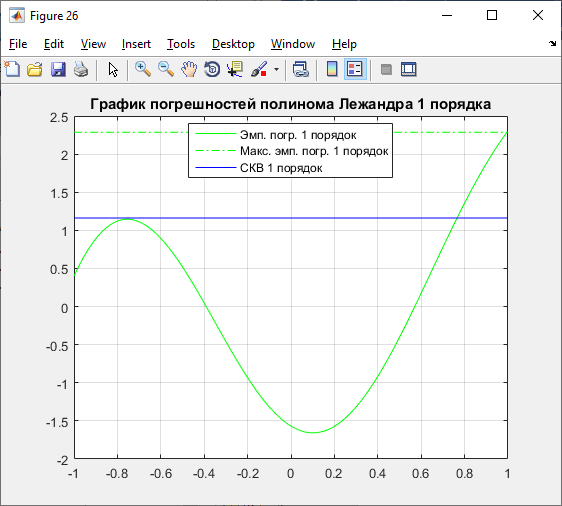
Рисунок 20 – Графики полинома и погрешностей 1 порядка
Б) 2 порядок:
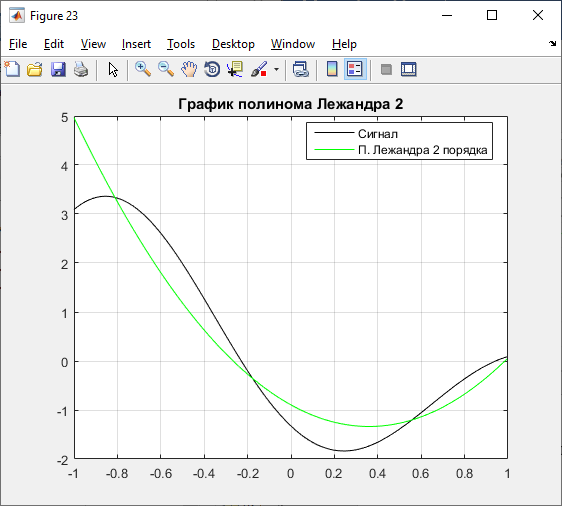
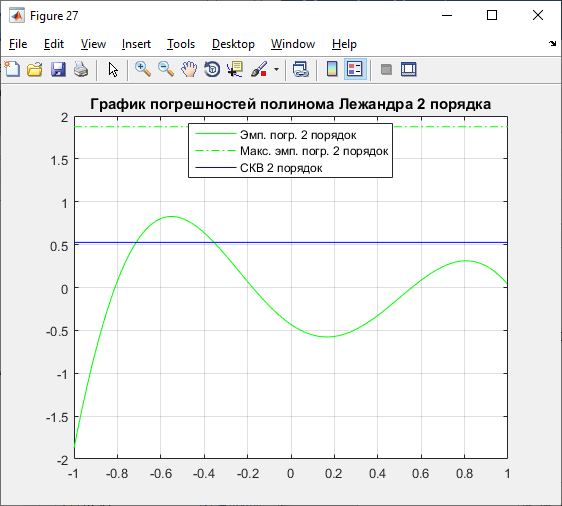
Рисунок 21 – Графики полинома и погрешностей 2 порядка
Б) 3 порядок:
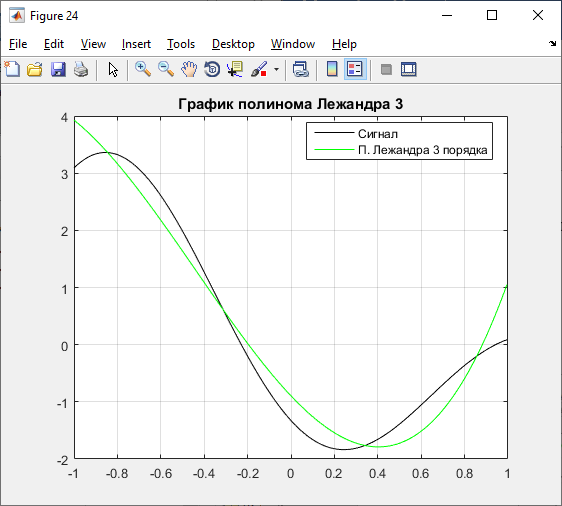
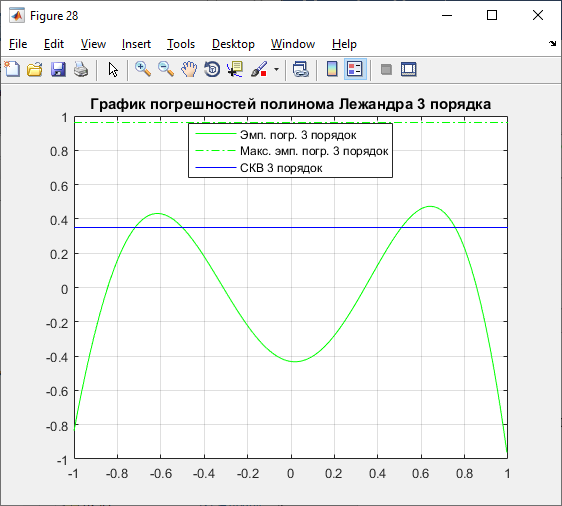
Рисунок 22 – Графики полинома и погрешностей 3 порядка
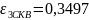
Из графиков видно, что вычисления сделаны
верно, так как значения
меньше максимальных значений эмпирических
погрешностей.
1.6 Описание сигнала по Уолшу
Функции Уолша ортогональны на интервале
Особенность функции Уолша заключается
в том, что они могут принимать только
два значения
или
.
Функции Уолша можно получить из функции
Радемахера, которые определяются на
интервале
выражением:
Из первых K функций Радемахера можно получить первые функции Уолша. Ортогональность функций Уолша можно использовать для описания сигналов в виде:
где коэффициенты
определяются выражением:
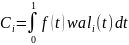
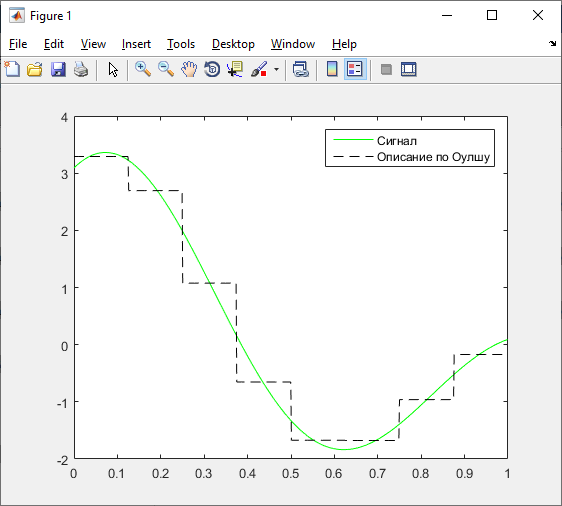
Рисунок 23 – Сигнал и описание сигнала по Уолшу
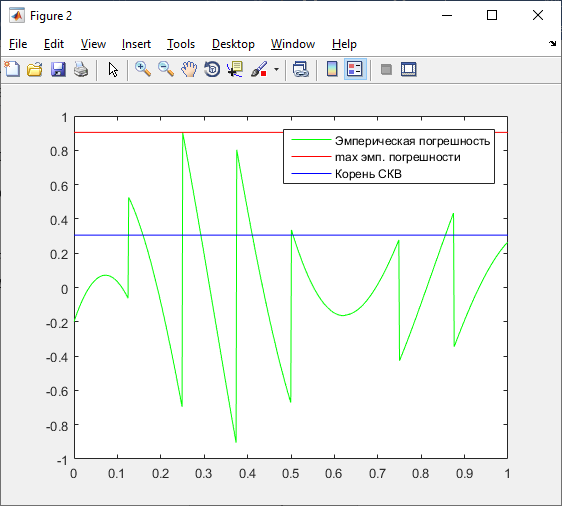
Рисунок 23 – График эмпирической, максимума эмпирической и СКВ погрешностей
1.7 Полиномы наилучшего приближения
Система уравнений, необходимая для
нахождения коэффициентов
полинома:
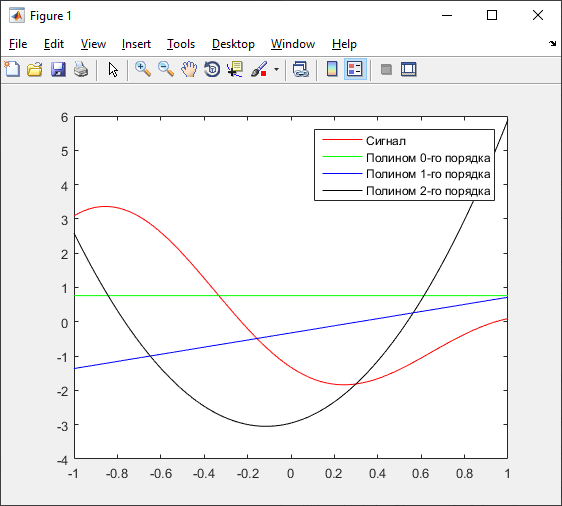
Рисунок 24 – График полиномов наилучшего приближения 0 – 2 порядков
А) 0 порядок:
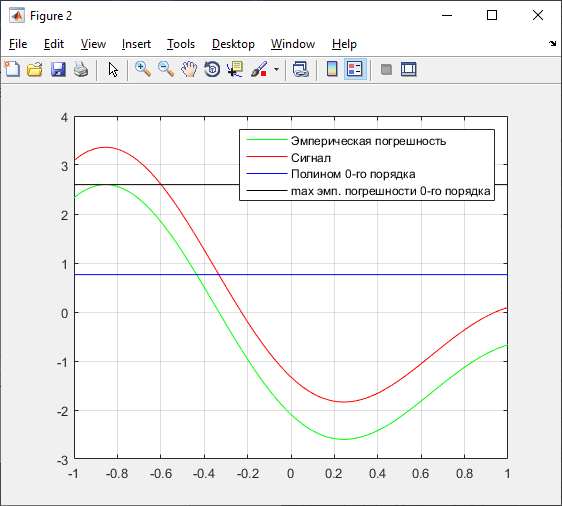
Рисунок 25 – График полинома наилучшего приближения 0 порядка
Б) 1 порядок:
Рисунок 26 – График полинома наилучшего приближения 1 порядка
В) 2 порядок:
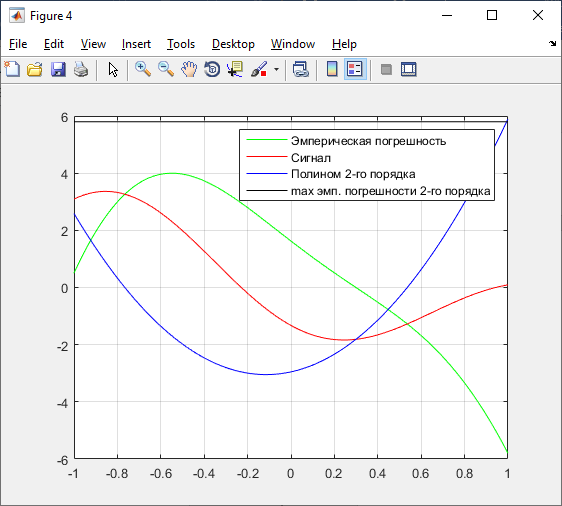
Рисунок 27 – График полинома наилучшего приближения 2 порядка
2. Спектральное описание сигнала
Для расчета спектра необходимо представить сигнал тригонометрическим рядом Фурье, использующим ортогональные функции:
Частота определяется через длину интервала:
Постоянная составляющая
,
амплитуды косинусов
и
определяется по формулам:
Сигнал можно представить рядом:
где
– постоянная составляющая,
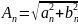– амплитуда
– й гармоники,
– фаза
– й гармоники.
Таблица 5 – Постоянные амплитуды
косинусов (
)
и синусов (
)
№ Гармоники |
a |
b |
№ Гармоники |
a |
b |
1 |
-1,5184 |
-1,9083 |
11 |
0,0020 |
-0,0871 |
2 |
-0,0688 |
0,5452 |
12 |
-0,0017 |
0,0798 |
3 |
0,0283 |
-0,3368 |
13 |
0,0014 |
-0,0736 |
4 |
-0,0155 |
0,2462 |
14 |
-0,0012 |
0,0683 |
5 |
-0,0098 |
-0,1947 |
15 |
0,0011 |
-0,0638 |
6 |
-0,0068 |
0,1613 |
16 |
-0,0009 |
0,0598 |
7 |
0,0050 |
-0,1377 |
17 |
-0,0008 |
-0,0562 |
8 |
-0,0038 |
0,1202 |
18 |
-0,0007 |
0,0531 |
9 |
0,0030 |
-0,1067 |
19 |
-0,0006 |
-0,0503 |
10 |
-0,0024 |
-0,0959 |
20 |
-0,0006 |
0,0478 |
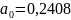
Рисунок 28 – Амплитудный спектр сигнала.
Таблица 6 – Фаза
№ гармоники |
|
№ гармоники |
|
1 |
2,2429 |
11 |
1,5479 |
2 |
4,5869 |
12 |
4,6914 |
3 |
1,4869 |
13 |
1,5514 |
4 |
4,6494 |
14 |
4,6944 |
5 |
1,5204 |
15 |
1,5540 |
6 |
4,6703 |
16 |
4,6966 |
7 |
1,5348 |
17 |
1,5560 |
8 |
4,6809 |
18 |
4,6984 |
9 |
1,5428 |
19 |
1,5575 |
10 |
4,6872 |
20 |
4,6998 |
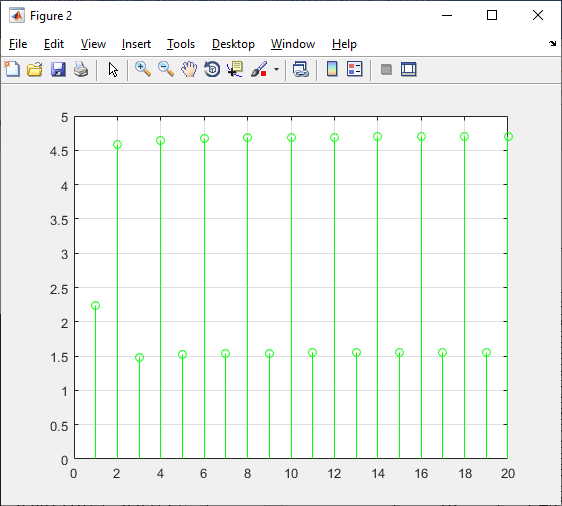
Рисунок 29 – Фазовый спектр сигнала.
Рисунок 30 – Восстановленный сигнал с помощью
спектрального описания.
Рисунок 31 – Погрешности описания.
Максимальная эмпирическая погрешность
СКВ
