
- •Содержание
- •Аннотация
- •Введение
- •1. Временное описание сигнала
- •1.1 Масштабирование сигнала
- •1.2 Описание сигнала по Лагранжу
- •1.3 Описание сигнала по Чебышеву
- •1.4 Описание сигнала по Тейлору
- •1.5 Описание сигнала по Лежандру
- •1.6 Описание сигнала по Уолшу
- •1.7 Полиномы наилучшего приближения
- •2. Спектральное описание сигнала
- •Заключение
- •Список использованных источников
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИИСТ
КУРСОВАЯ РАБОТА
по дисциплине «Преобразование измерительных сигналов»
Тема: Временное описание сигналов
Вариант № 27
Студент гр. 9587 |
|
Медведев Г.Н. |
Преподаватель |
|
Романцова Н.В. |
Санкт-Петербург
2022
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Студент: Медведев Г.Н. |
||
Группа 9587 |
||
Тема работы: Временное описание сигналов |
||
Исходные данные:
Вариант № 27 Описать
сигнал на интервале
1) Лагранжа; 2) Лагранжа с использованием узловых точек Чебышева; 3) Тейлора; 4) Лежандра; 5) Уолша; 6) Полиномом наилучшего приближения; 7) Спектральным описанием сигнала; |
||
Содержание пояснительной записки: «Содержание», «Введение», «Заключение», «Список использованных источников». |
||
Предполагаемый объем пояснительной записки: Не менее 15 страниц. |
||
Дата выдачи задания: 11.10.2022 |
||
Дата сдачи отчёта: |
||
Дата защиты отчёта: |
||
Студент |
|
Медведев Г.Н. |
Преподаватель |
|
Романцова Н.В. |
Содержание
Y
Аннотация
Целью курсовой работы является изучение различных методов временного описания сигналов. В ходе выполнения курсовой работы сигнал был описан с помощью полиномов Лагранжа, Тейлора, Лежандра, наилучшего приближения, по Чебышеву, по Уолшу и спектральным описанием. Для расчетов и построения графиков была выбрана среда программирования Matlab. В результате были построены графики, посчитаны погрешности и сделаны выводы.
SUMMARY
The purpose of the course work is to study various methods of time description of signals. During the course work, the signal was described using Lagrange, Taylor, Legendre polynomials, the best approximation, Chebyshev, Walsh and spectral description. The Matlab programming environment was chosen for calculations and plotting. As a result, graphs were constructed, errors were calculated and conclusions were drawn.
Введение
Изучение различных методов временного описания сигналов позволяет закрепить знания, полученные при изучении основных разделов курса «преобразование измерительных сигналов».
1. Временное описание сигнала
1.1 Масштабирование сигнала
Исходный сигнал:

Описание сигналов удобнее вести не в
реальном времени
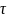 ,
а в нормированной безразмерной переменной
t интервале [-1, 1], для этого
масштабирования необходимо произвести
линейное преобразование аргумента.
,
а в нормированной безразмерной переменной
t интервале [-1, 1], для этого
масштабирования необходимо произвести
линейное преобразование аргумента.
Переменная t и переменная связаны зависимостью:
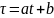
где
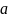 и
и
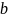 – постоянные коэффициенты, определяемые
из условия
– постоянные коэффициенты, определяемые
из условия

Отсюда следует, что

Нормированный сигнал:


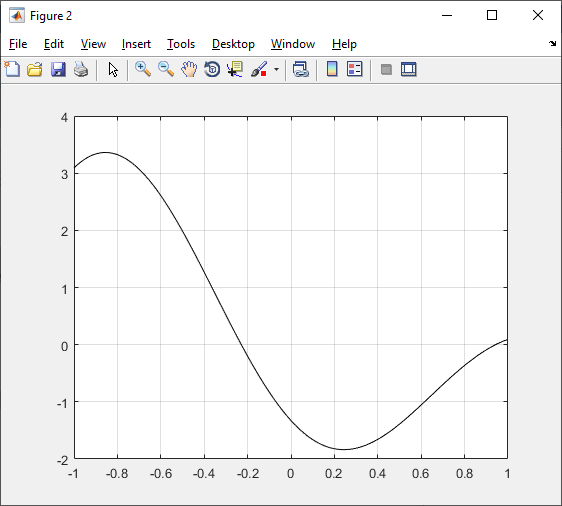
Рисунок 1 – Графики исходного и нормированного сигналов
1.2 Описание сигнала по Лагранжу
Описание сигнала
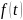 по Лагранжу осуществляется с помощью
интерполяционного полинома Лагранжа,
который имеет вид:
по Лагранжу осуществляется с помощью
интерполяционного полинома Лагранжа,
который имеет вид:
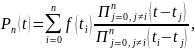
где n – порядок описывающего
полинома,
 – порядковые номера узловых точек
(узлов интерполяции),
– порядковые номера узловых точек
(узлов интерполяции),
 – координаты узловых точек.
– координаты узловых точек.
Аналитическое выражение для полиномов Лагранжа представляется в виде:

где
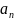 – постоянные коэффициенты.
– постоянные коэффициенты.
Полиномы:
А) 0 порядок:
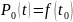
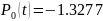

Рисунок 2 – График полинома Лагранжа 0 порядка
Б) 1 порядок:

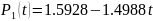
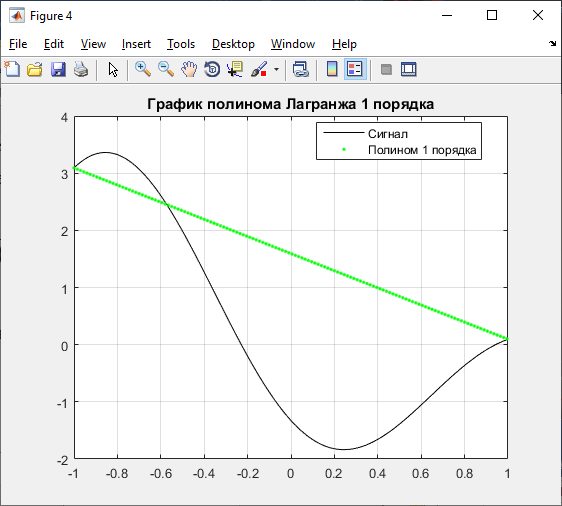
Рисунок 2 – График полинома Лагранжа 1 порядка
В) 2 порядок:



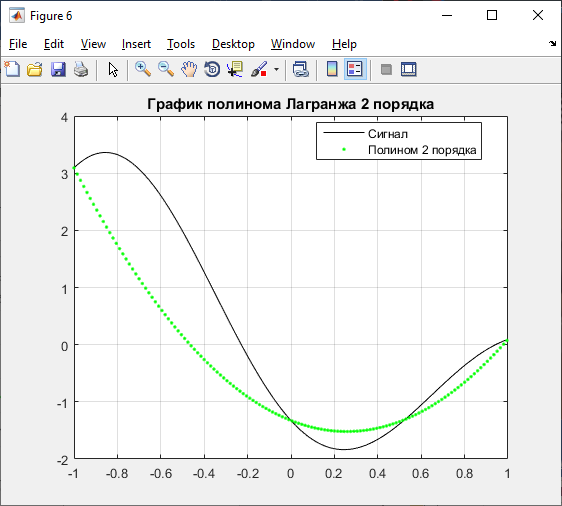
Рисунок 3 – График полинома Лагранжа 2 порядка
Г) 3 порядок:
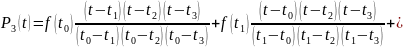
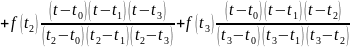

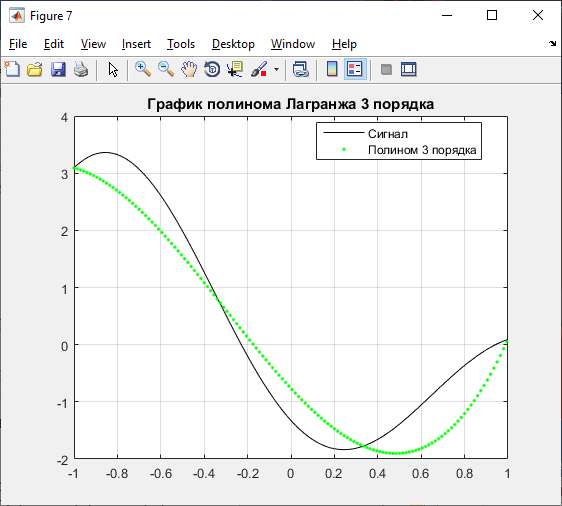
Рисунок 4 – График полинома Лагранжа 3 порядка
Таблица 1 – Координаты узловых точек
Порядок |
t0 |
t1 |
t2 |
t3 |
0 |
0 |
|
|
|
1 |
-1 |
1 |
|
|
2 |
-1 |
0 |
1 |
|
3 |
-1 |
-1/3 |
1/3 |
1 |
Порядок |
f0 |
f1 |
f2 |
f3 |
0 |
-1.3277 |
|
|
|
1 |
3.0916 |
0.094 |
|
|
2 |
3.0916 |
-1.327 |
0.094 |
|
3 |
3.0916 |
0.767 |
-1.7745 |
0.094 |
Эмпирическая погрешность, найденная из графиков для i-го полинома:
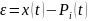
Оценка максимальной погрешности для i-го полинома:

где
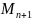 – модуль-максимум (
– модуль-максимум ( )-й
производной сигнала на рассматриваемом
интервале.
)-й
производной сигнала на рассматриваемом
интервале.
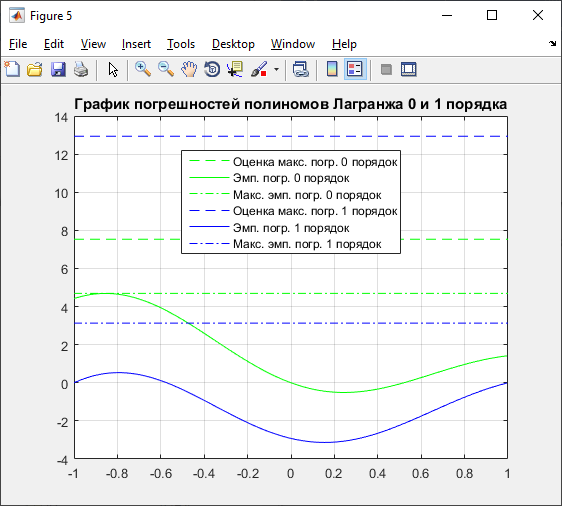
Рисунок 5 – Графики погрешностей полиномов 0 и 1 порядков
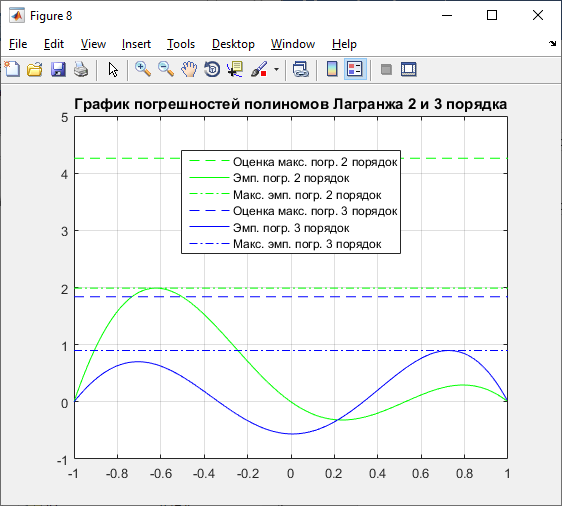
Рисунок 6 – Графики погрешностей полиномов 2 и 3 порядков
Таблица 2 – Максимумы эмпирической погрешности и оценка максимальной погрешности
Порядок |
Максимум эмпирической погрешности |
Оценка максимальной погрешности |
0 |
4.6886 |
7.5322 |
1 |
3.1309 |
12.9383 |
2 |
1.9893 |
4.2611 |
3 |
0.8978 |
1.8386 |
Из графиков видно, что значения эмпирической погрешности не превышают значения оценки максимальной погрешности, что свидетельствует о правильности вычислений.


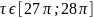 следующими методами:
следующими методами: