лаба5

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИИСТ

отчет

по лабораторной работе №5

по дисциплине «Преобразование измерительных сигналов»

Тема: СПЕКТРАЛЬНОЕ ОПИСАНИЕ СИГНАЛОВ В MATLAB.

ПОИСК КОМПЛЕКСНОГО СПЕКТРА И СПЕКТРАЛЬНОЙ ПЛОТНОСТИ

Студенты гр. 9587		Медведев Г.Н.
		Постникова Е.И.
Преподаватель		Романцова Н.В.

Санкт-Петербург

2022

Цель работы:

Ознакомиться с комплексным спектром сигнала и спектральной плотностью, приобрести навыки их нахождения и построения в MATLAB.

Основные теоретические положения.

Экспоненциальный ряд Фурье имеет вид:

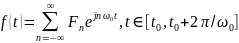
Коэффициенты разложения являются комплексными числами и определяются из выражения:

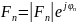
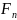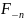Для фазы вектора выполняется условие , таким образом, комплексные числа и на положительных и отрицательных частотах отличаются только знаком фазы и являются комплексно-сопряженными числами.

Коэффициент экспоненциального ряда можно записать следующим образом:

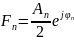
Значение комплексных коэффициентов вычисляется следующим образом:

Спектральная плотность – это непрерывная функция частоты:

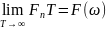
Спектральная плотность вычисляется по формуле:

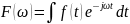
Обработка результатов

Код программы:

T1 = 0;

T2 = pi;

t = T1: 0.01: T2;

w0 = 2 * pi / (T2 - T1);

T = T2 - T1;

j = sqrt(-1);

a0 = 1 / T * integral(@f, T1, T2);

n = 20;

for i = 1: 1: n+1

cosn = @(t) (-1+5*sin(2*t+90)-3*cos(4*t+10)+0.09*t.^2) .* cos((i) * t * w0);

sinn = @(t) (-1+5*sin(2*t+90)-3*cos(4*t+10)+0.09*t.^2) .* sin((i) * t * w0);

a(i) = 2 / T * integral(cosn, T1, T2);

b(i) = 2 / T * integral(sinn, T1, T2);

end

F = a0;

for i = 1: 1: n

An(i) = sqrt(a(i)^2 + b(i)^2);

if (a(i) >=0)

fin(i) = -atan(b(i) / a(i));

else

fin(i) = -atan(b(i)/a(i)) + pi;

end

F = F + An(i) * cos(i * w0 * t + fin(i));

end

for i = 1: 1: n

FnMod(i) = An(i)/2;

Fn(i) = 1/T * integral(@(t) (-1+5*sin(2*t+90)-3*cos(4*t+10)+0.09*t.^2).*exp(-j*i*w0*t), T1, T2);

end

for i = 1: 1: 2 * n +1

if(i<21)

finLong(i) = -fin(0 - (i - 1 - n));

FnModLong(i) = FnMod(0 - (i - 1 - n));

FnLong(i) = Fn(0 - (i - 1 - n));

elseif(i>21)

finLong(i) = fin(i - n - 1);

FnModLong(i) = FnMod(i - n - 1);

FnLong(i) = Fn(i - n - 1);

else

finLong(i) = 0;

FnModLong(i) = a0;

FnLong(i) = a0;

end

end

figure(1);

stem(0, a0, '-b');

hold on;

stem(1: 1: n, An, '-b');

hold on;

stem(-20: 1: 20, FnModLong, '-.r', 'LineWidth', 1);

hold on;

grid on;

figure(2);

stem(-20 :1 : 20, finLong);

hold on;

grid on;

figure(3);

hold on;

grid on;

hold on;

ff = a0;

for i = 1: 1: 20

ff = ff + 2 * Fn(i) * exp(j * w0 * i * t);

end

ex = a0^2;

for i = 1: 1: n

an = An(i);

ex = ex + (an^2) / 2;

end

es = sqrt((1 - ex / (1/T * integral(@f2, T1, T2))).^2);

plot(t, f(t), 'y','LineWidth', 3);

hold on;

plot(t, ff, ':b','LineWidth', 3);

hold on;

legend('Сигнал', 'Восстановленный сигнал');

figure(4);

plot(t, f(t) - ff);

hold on;

e0 = max(abs(real(f(t) - ff)));

plot([T1 T2], [e0 e0], '--g');

hold on;

plot([T1 T2], [es es], '--b');

hold on;

legend('Эмпирическая погрешность', 'Максимум эмпирической погрешности', 'СКВ погрешность');

function y = f(t)

y = -1+5*sin(2*t+90)-3*cos(4*t+10)+0.09*t.^2;

end

function y = f2(t)

y = (-1+5*sin(2*t+90)-3*cos(4*t+10)+0.09*t.^2).^2;

end

Результаты выполнения программы:

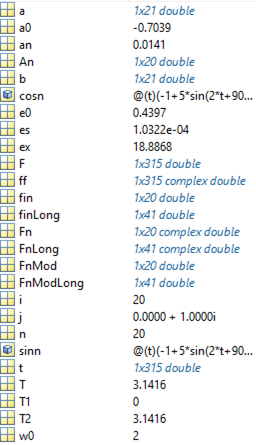
Рисунок 1 – Рабочее пространство программы

Рисунок 1 – График комплексно – амплитудного спектра сигнала

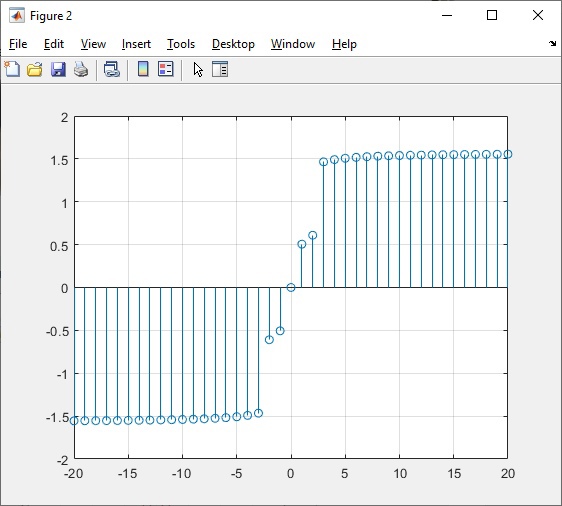
Рисунок 2 – График фазового спектра сигнала

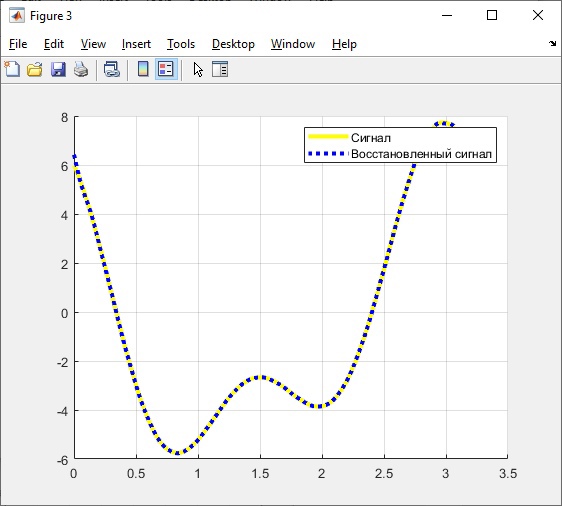
Рисунок 3 – График первоначального и восстановленного сигнала

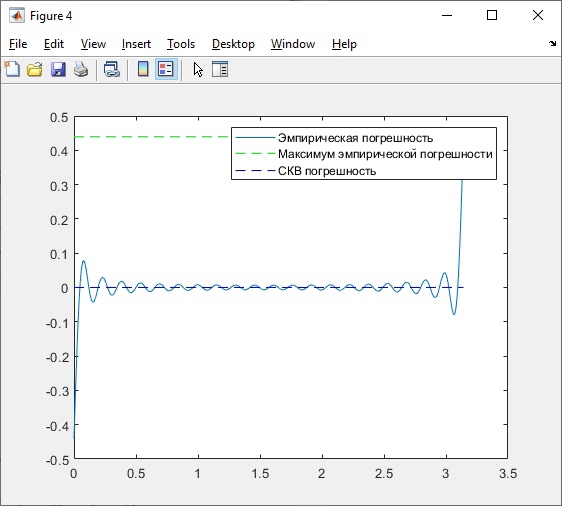
Рисунок 4 – График эмпирической погрешности и СКВ

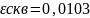
Выводы: в ходе выполнения лабораторной работы было произведено ознакомление с комплексным спектром сигнала и спектральной плотностью, были построены графики комплексно – амплитудного спектра сигнала, фазового спектра сигнала, первоначального и восстановленного сигнала, эмпирической погрешности и СКВ, по графику были определены 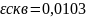и .