лаб1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИИСТ

отчет

по лабораторной работе №1

по дисциплине «Преобразование измерительных сигналов»

Тема: Описание сигнала полиномами Лагранжа в графические программирования LabView

Студент гр. 9587		Медведев Г.Н.
Преподаватель		Романцова Н.В.

Санкт-Петербург

2022

Цель работы.

Ознакомиться с математическим аппаратом полиномов Лагранжа в среде графического программирования LabVIEW.

Основные теоретические положения

Полиномом Лагранжа n-го порядка называется многочлен вида

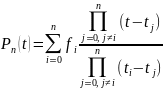
Полином Лагранжа содержит значения сигнала в (n + 1) узловой точке (точки, в которых описание должно совпасть с сигналом) 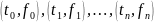, где все 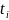различны; i, j – порядковые номера узлов интерполяции.

Основные достоинства описания:

1. Построенная функция имеет непрерывные производные любого порядка в каждой точке.

2. Отсутствует необходимость предварительных расчетов (выражение для полинома записывается сразу по координатам узловых точек).

3. Математический аппарат Лагранжа исключительно удобен при одновременном обслуживание большого количества параметров и удачном выборе параметрической переменной.

Основные недостатки описания:

1. При росте числа узловых точек (степени полинома Лагранжа) необходим полный пересчет многочлена (полином Ньютона исключает данный недостаток, помогая сохранить расчеты при увеличении количества узловых точек).

2. Замена даже одной точки из массива узловых точек приводит к перерасчету полинома.

3. Требует значительных временных затрат.

Оценка сверху максимальной погрешности описания сигнала полиномом Лагранжа n-го порядка 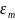рассчитывается по формуле:

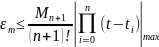
где 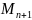– модуль-максимум (n+1)-й производной сигнала f(t) на рассматриваемом интервале.

Максимальное значение погрешности описания сигнала рассчитывается по формуле:

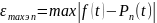
где n – порядок полинома, описывающего сигнал, t принадлежит интервалу описания сигнала.

Обработка результатов эксперимента

1. Приведем формулы, выведенные для описания сигнала полиномами Лагранжа 0-ого, 1-ого, 2-ого и 3-ого порядков соответственно:

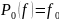
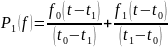
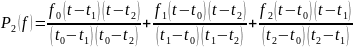
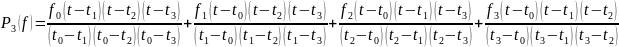
2. Приведем лицевую панель (с графиком) и блок диаграмму (с кодом программы) в LabView для полиномов Лагранжа 0-ого, 1-ого, 2-ого и 3-ого порядков:

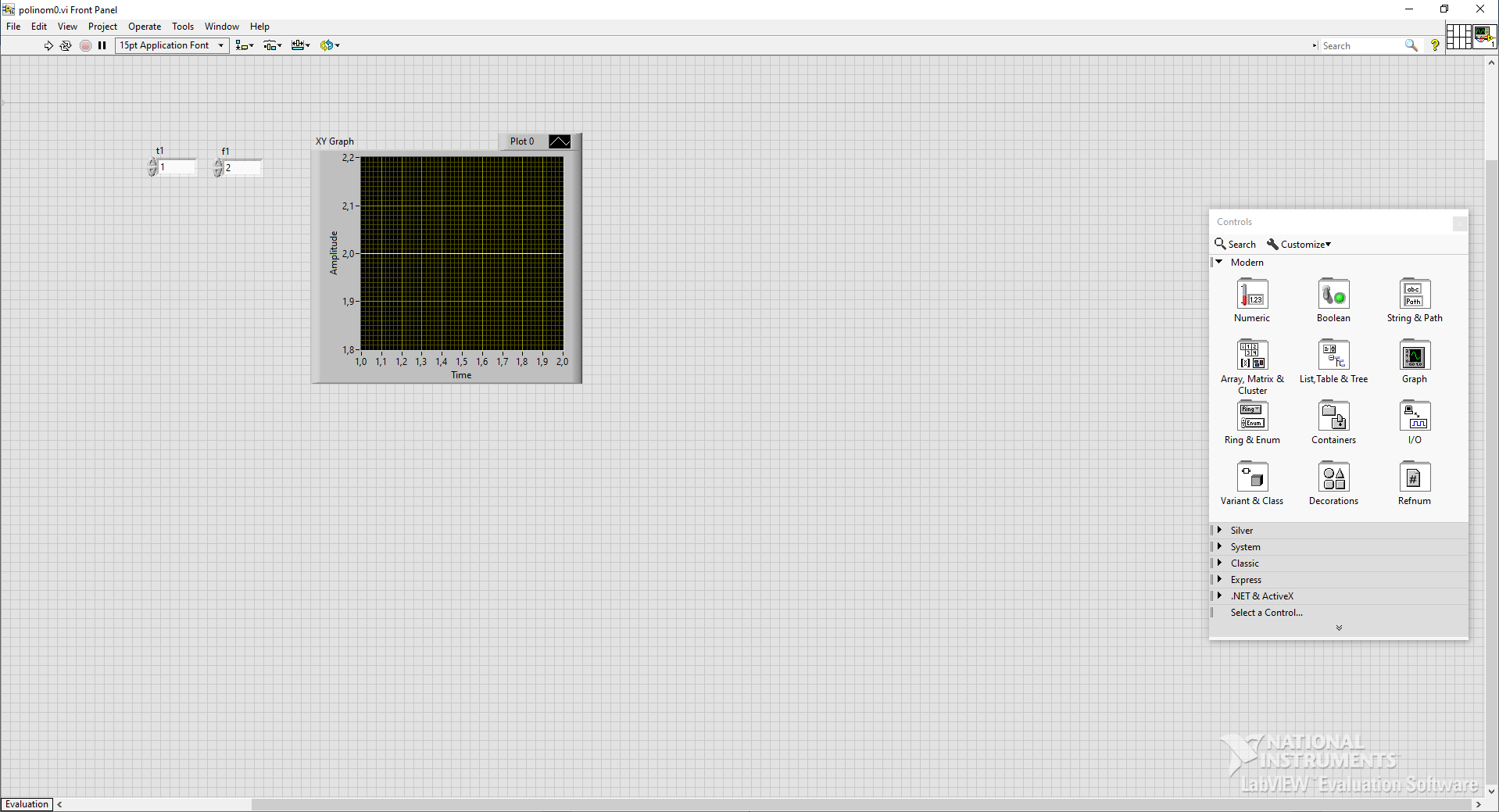
Рисунок 1 – лицевая панель с графиком полинома Лагранжа 0-ого порядка

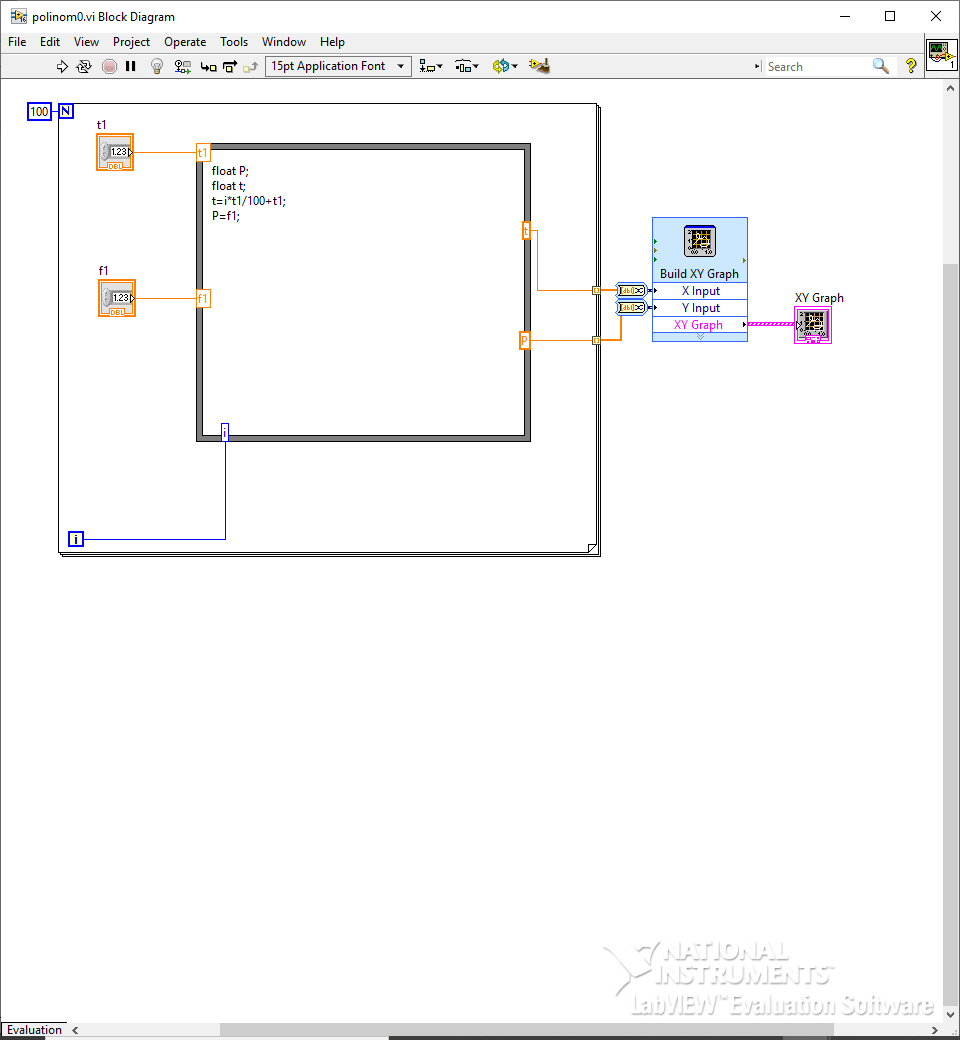
Рисунок 2 – блок диаграмма с кодом полинома Лагранжа 0-ого порядка

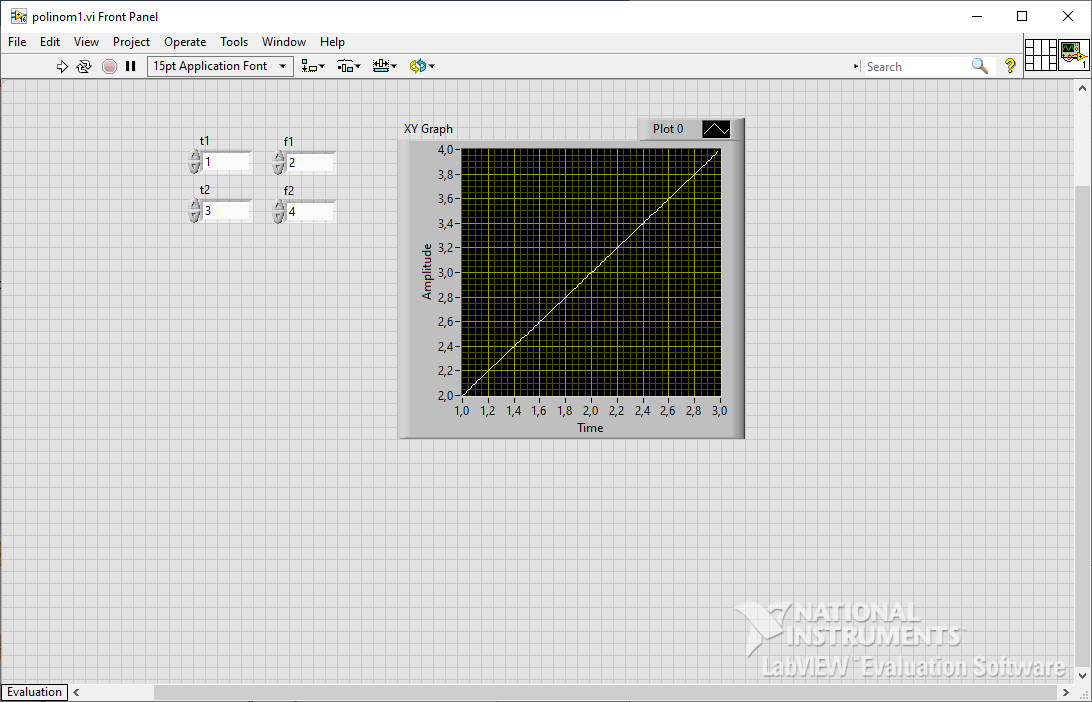
Рисунок 3 – лицевая панель с графиком полинома Лагранжа 1-ого порядка

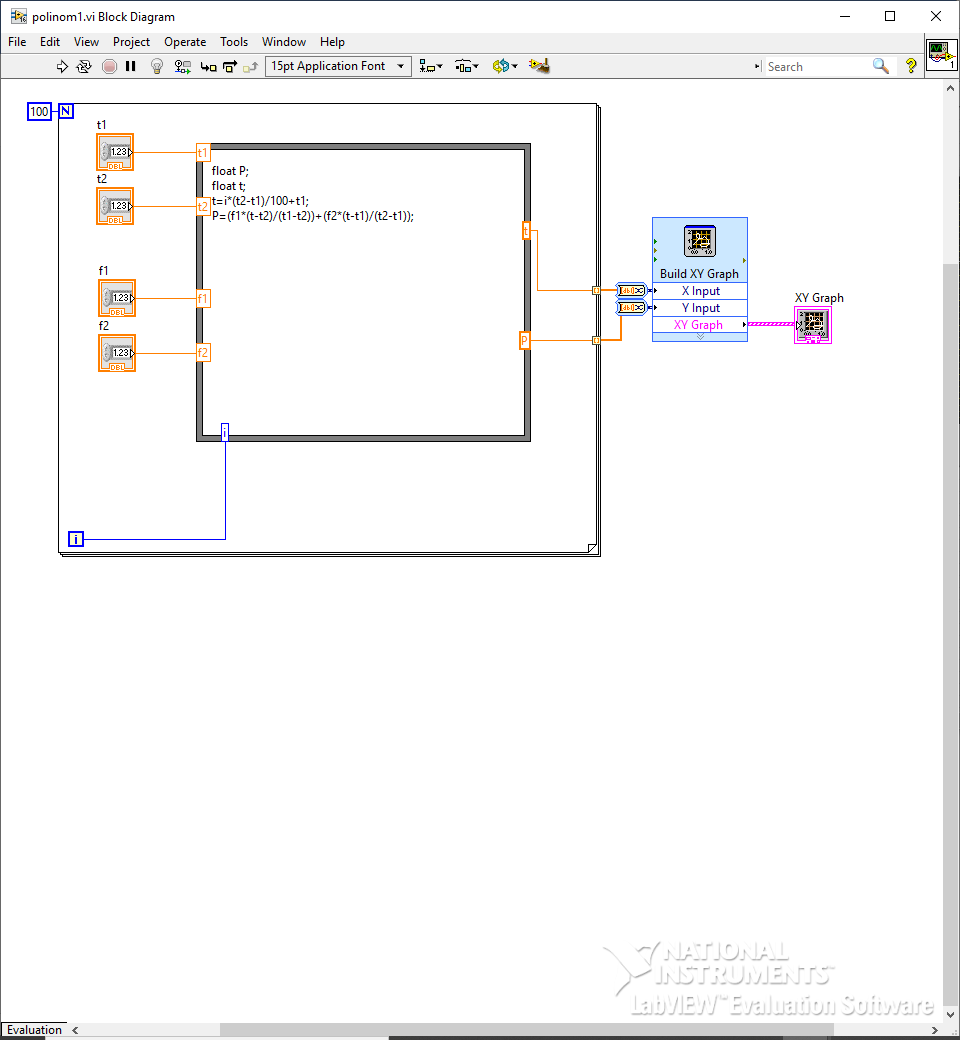
Рисунок 4 – блок диаграмма с кодом полинома Лагранжа 1-ого порядка

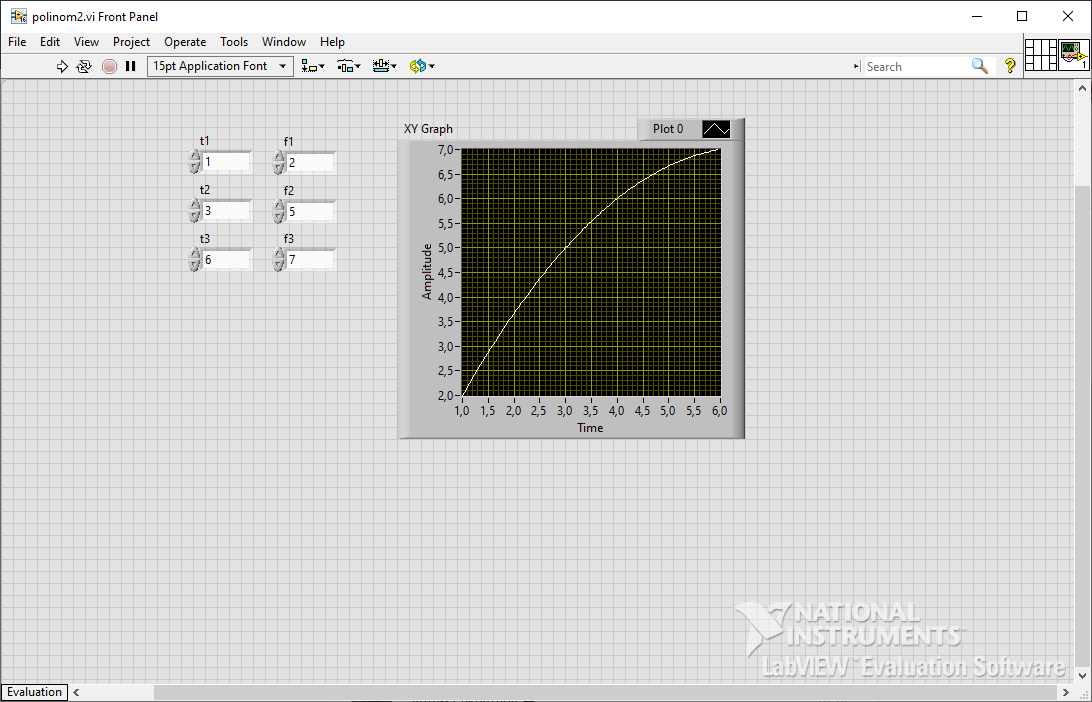
Рисунок 5 – лицевая панель с графиком полинома Лагранжа 2-ого порядка

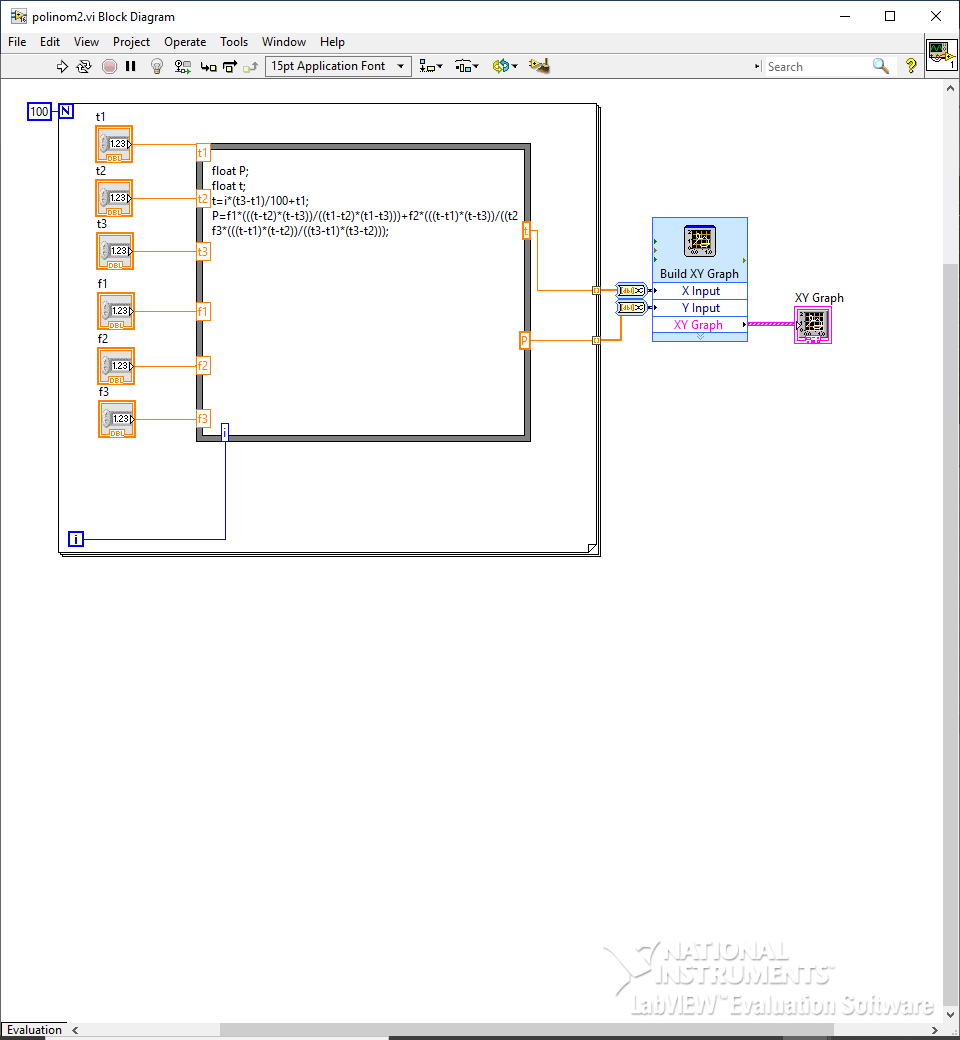
Рисунок 6 – блок диаграмма с кодом полинома Лагранжа 2-ого порядка

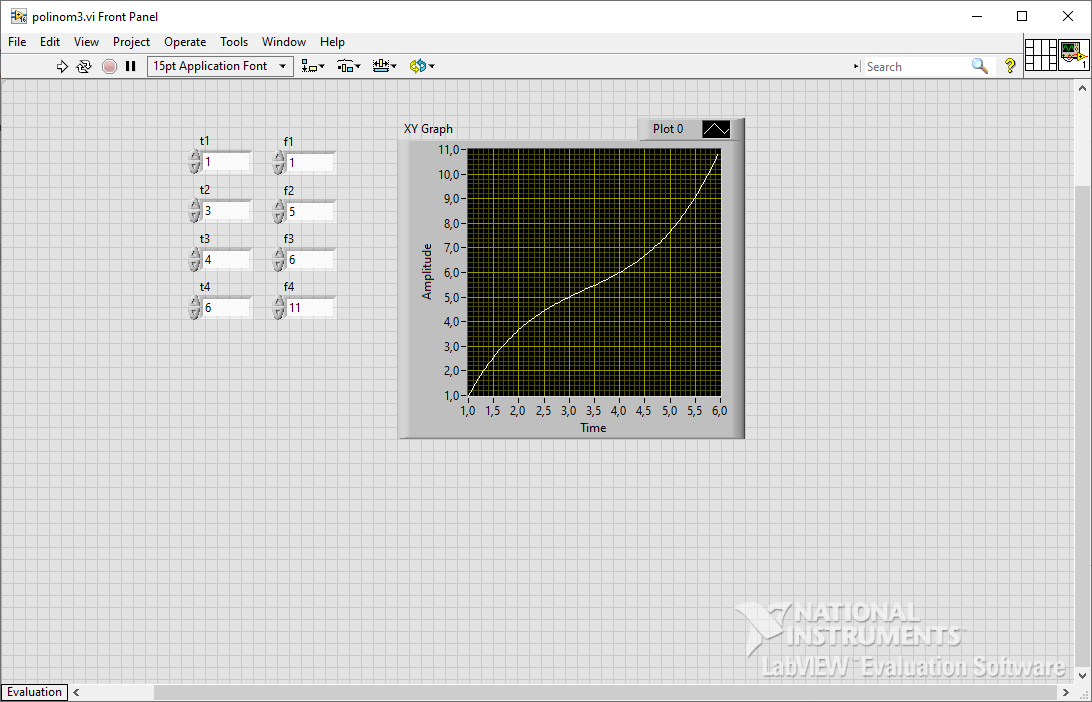
Рисунок 7 – лицевая панель с графиком полинома Лагранжа 3-ого порядка

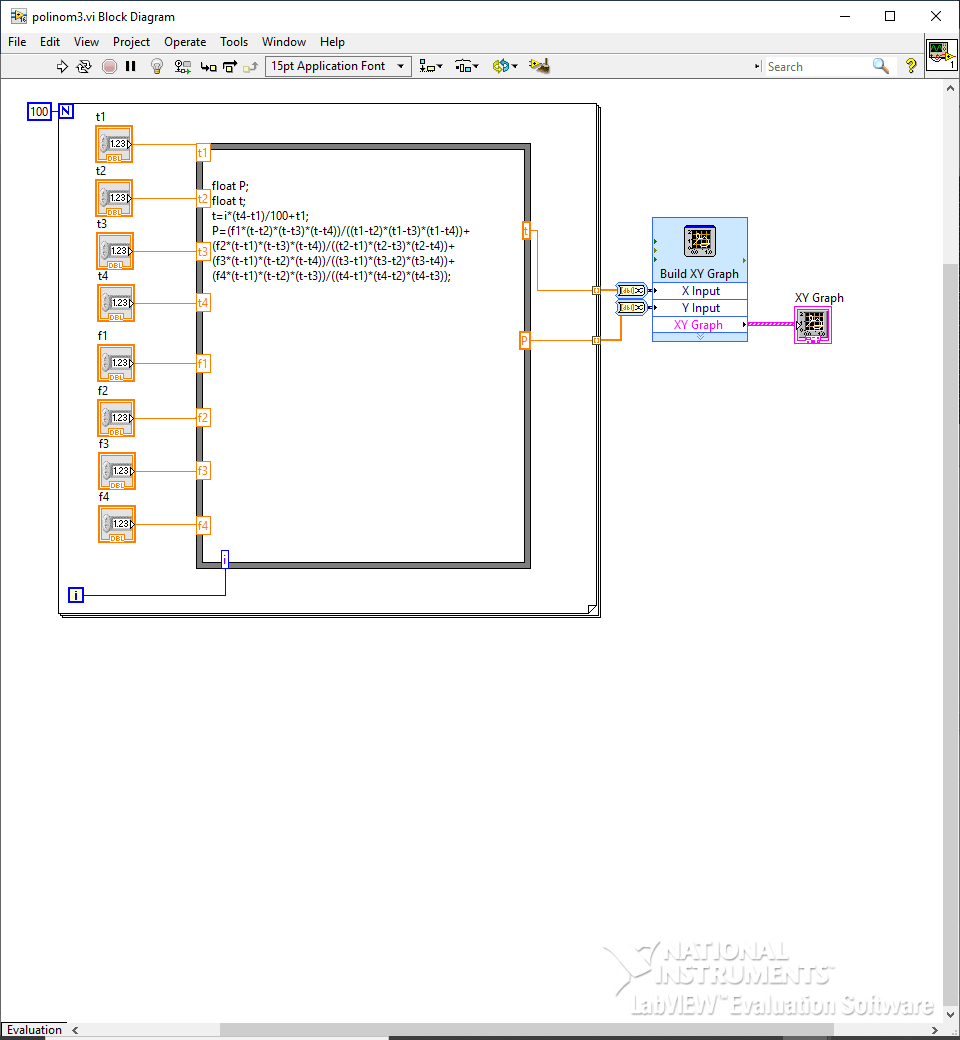
Рисунок 8 – блок диаграмма с кодом полинома Лагранжа 3-ого порядка

Вывод: в ходе выполнения лабораторной работы было произведено ознакомление с математическим аппаратом полиномов Лагранжа в среде графического программирования LabView; были сделаны программы для построения полиномов Лагранжа 0-ого, 1-ого, 2-ого и 3-ого порядков; были приведены коды программ и графики полиномов.