28. Условия неискаженной передачи сигналов.

1) АЧХ = const

2) Линейность ФЧХ

tg(α) ФЧХ будет определять задержку сигнала.

Если выполнится первое условие, то выполнится и второе.

Считается, что сигнал x(t) проходит через некоторую систему без искажения, если происходит только изменение масштаба и сдвиг во времени. При этом форма сигнала не изменяется. Если начало отсчета времени отнести к моменту возникновения входного сигнала x(t), то неискаженный сигнал на выходе системы должен иметь вид y=k*x(t-τ), где k - постоянный коэффициент.

Учитывая свойства линейности и временного сдвига, найдем спектральную характеристику выходного сигнала:

Следовательно, неискажающая система должна иметь частотную передаточную функцию

Из этого выражения видно, что система, удовлетворяющая условиям неискаженного преобразования сигнала, имеет не зависящую от частоты амплитудно-частотную характеристику (АЧХ = const)

и фазо-частотную характеристику, линейно изменяющую с частотой (линейность ФЧХ):

Частотные характеристики, построенные по выражениям.

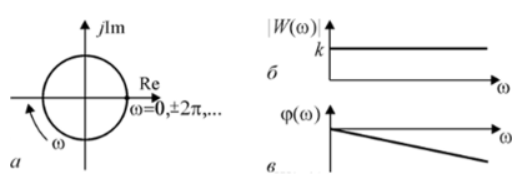
Частотные характеристики системы, передающей сигнал без искажения: а - АФЧХ; б - АЧХ, в – ФЧХ

Задержка τ гармонического сигнала, создаваемая системой с частотной передаточной функцией, определяется наклоном ФЧХ:

29. Методы нахождения частотных характеристик.

Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного сигнала, называются частотными характеристиками (ЧХ). Анализ ЧХ системы с целью исследования ее динамических свойств называется частотным анализом.

По аналогии с передаточной функцией можно записать:

.

W(j), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией.

W(j) есть комплексная функция, поэтому:

где P() - вещественная ЧХ (ВЧХ); Q() - мнимая ЧХ (МЧХ); А() - амплитудная ЧХ (АЧХ):  () - фазовая ЧХ (ФЧХ). АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной:

Если W(j) изобразить вектором на комплексной плоскости, то при изменении  от 0 до +   его конец будет вычерчивать кривую, называемую годографом вектора W(j), или амплитудно-фазовую частотную характеристику (АФЧХ). 

Логарифмические частотные характеристики (ЛЧХ): логарифмическая амплитудная ЧХ (ЛАЧХ) L() и логарифмическая фазовая ЧХ (ЛФЧХ)  (). Они получаются путем логарифмирования передаточной функции:

ЛАЧХ: L() = 20lgA().

lg(P₂/P₁) = lg(A₂²/A₁²) = 20lg(A₂/A₁).

22