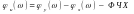- •1. Описание сигналов по Лагранжу. Оценка погрешности.
- •2. Описание сигналов по Ньютону. Оценка погрешности.
- •3. Описание сигналов по Тейлору. Оценка погрешности.
- •4. Оценка погрешности полиномиального описания сигналов в равномерной метрике.
- •5. Полиномы Чебышева. Свойство старших коэффициентов и свойство корней.
- •6. Полиномы Чебышева. Свойство экстремумов и фундаментальное свойство.
- •7. Описание сигналов по Чебышеву. Погрешность описания.
- •9. Описание сигналов в среднеквадратической метрике. Ортогональные функции.
- •10. Погрешность описания сигналов ортогональными функциями.
- •11. Ортогональные функции Уолша.
- •12. Действительный спектр сигналов.
- •13. Комплексный спектр сигналов.
- •20. Свойство временного и частотного сдвига. Теорема о модуляции.
- •21. Свойство. Дифференцирования.
- •22. Свойство свёртки во времени.
- •23. Свёртка сигналов с предварительным дифференцированием.
- •24. Свойство свёртки по частоте.
- •25. Свойство интегрирования.
- •26. Спектральная плотность энергии и мощности сигналов.
- •27. Частотные характеристики линейных измерительных цепей.
- •28. Условия неискаженной передачи сигналов.
- •29. Методы нахождения частотных характеристик.
21. Свойство. Дифференцирования.
Если f(t) F() , то d/dt f(t) j F().
Доказательство: так как по обратному преобразованию Фурье
![]()
то дифференцируя это выражение по t и меняя порядок дифференцирования и интегрирования, получаем:
внесение знака дифференцирования под интеграл возможно, так как интегрирование ведется по переменной в то время, как дифференцирование осуществляется по переменной t. Что и требовалось доказать.
При n-кратном дифференцировании:
Свойство дифференцирования широко используется для нахождения спектральных плотностей кусочно-линейных сигналов.
22. Свойство свёртки во времени.
Путем свертки двух известных сигналов f1(t), f2(t) можно получить сигнал f(t). Процедура свертки символически обозначается «*». При перестановке индексов 1 и 2 в записи операции свертки результат не меняется, однако меняется промежуточные записи интегралов:
![]()
Операция свертки – это интегральная операция:
Во временной области принято использовать переменную t, в интегралах свертки буква t формально заменяется на τ.
Конкретные пределы интегрирования определяются видом сигналов. Считая, что сигналы существуют во времени t >0 и учитывая, что бесконечные пределы интегрирования символически показывают, что свертку необходимо рассматривать на бесконечном сдвиге t, операцию свертки можно записать в следующем виде:
Свойство свертки:
Спектральная плотность свертки двух сигналов рана произведению спектральных плотностей.
Строгое доказательство:
23. Свёртка сигналов с предварительным дифференцированием.
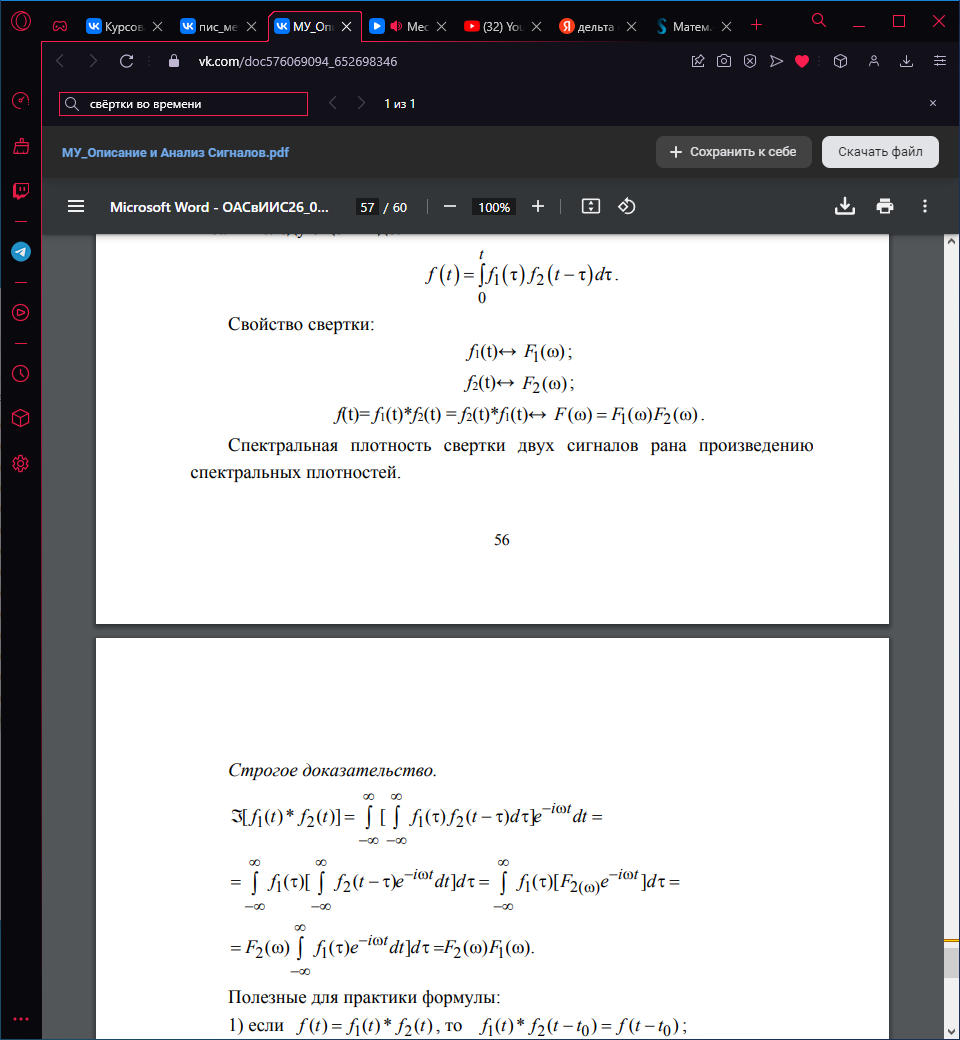
Свертка с δ(t) – самая простая для расчета. Продифференцируем один из прямоугольных импульсов, получим две δ(t) на возрастающем и убывающих фронтах. Получим свертку прямоугольных сигналов.

Продифференцируем прямоугольник f2(t). Свернем сигнал f1(t) с f'2(t).
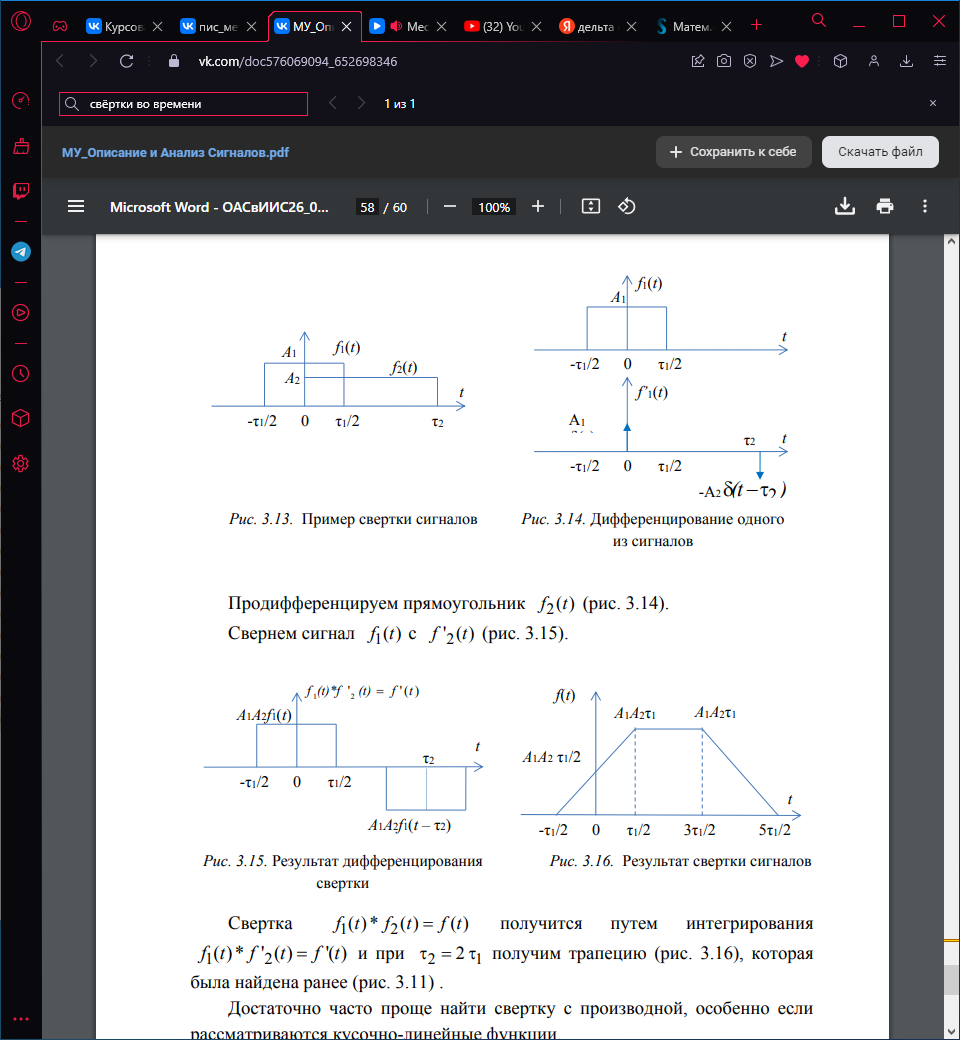
Свертка f1(t) * f2(t) = f(t) получится путем интегрирования f1(t) * f'2(t) = f' (t) и при 2 2 1 получим трапецию.
Достаточно часто проще найти свертку с производной, особенно если рассматриваются кусочно-линейные функции.
24. Свойство свёртки по частоте.
Если
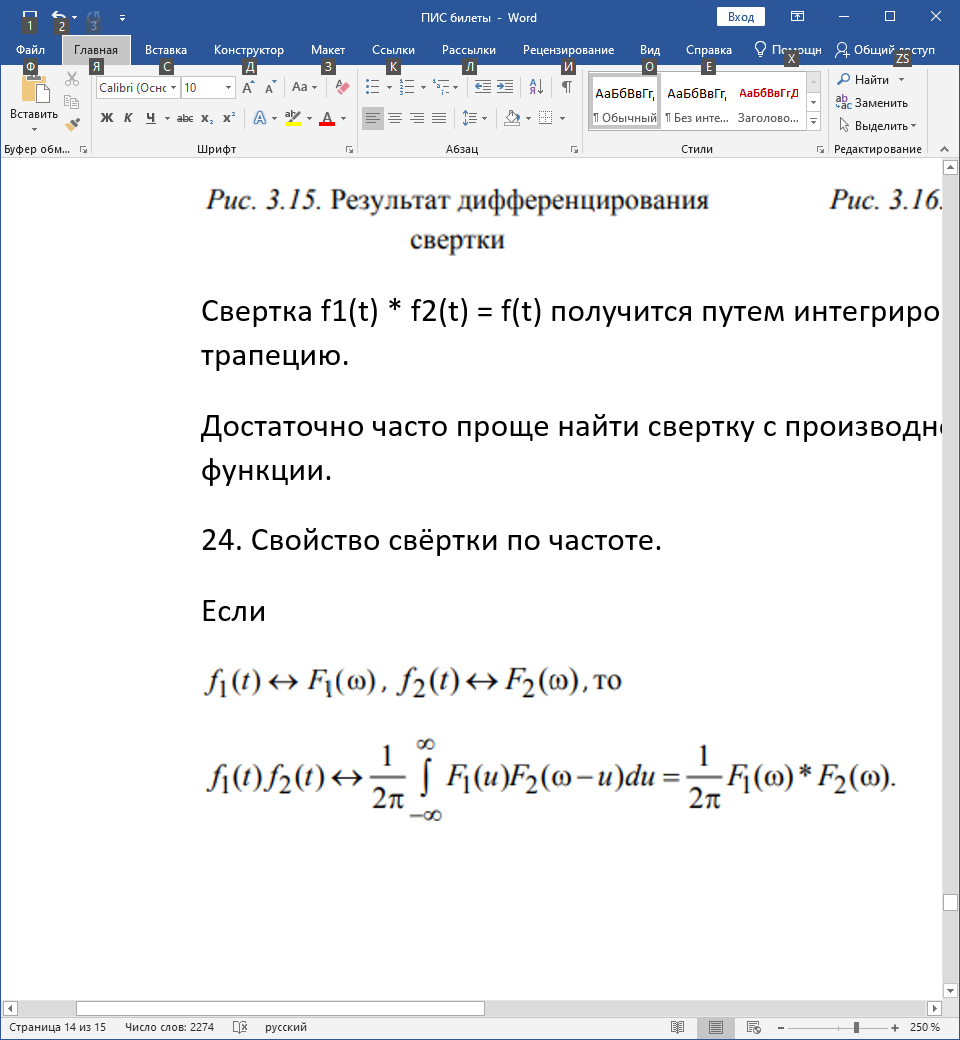
Доказательство:

25. Свойство интегрирования.
Если
![]()
Доказательство: рассмотрим свертку 1(t) и f(t):
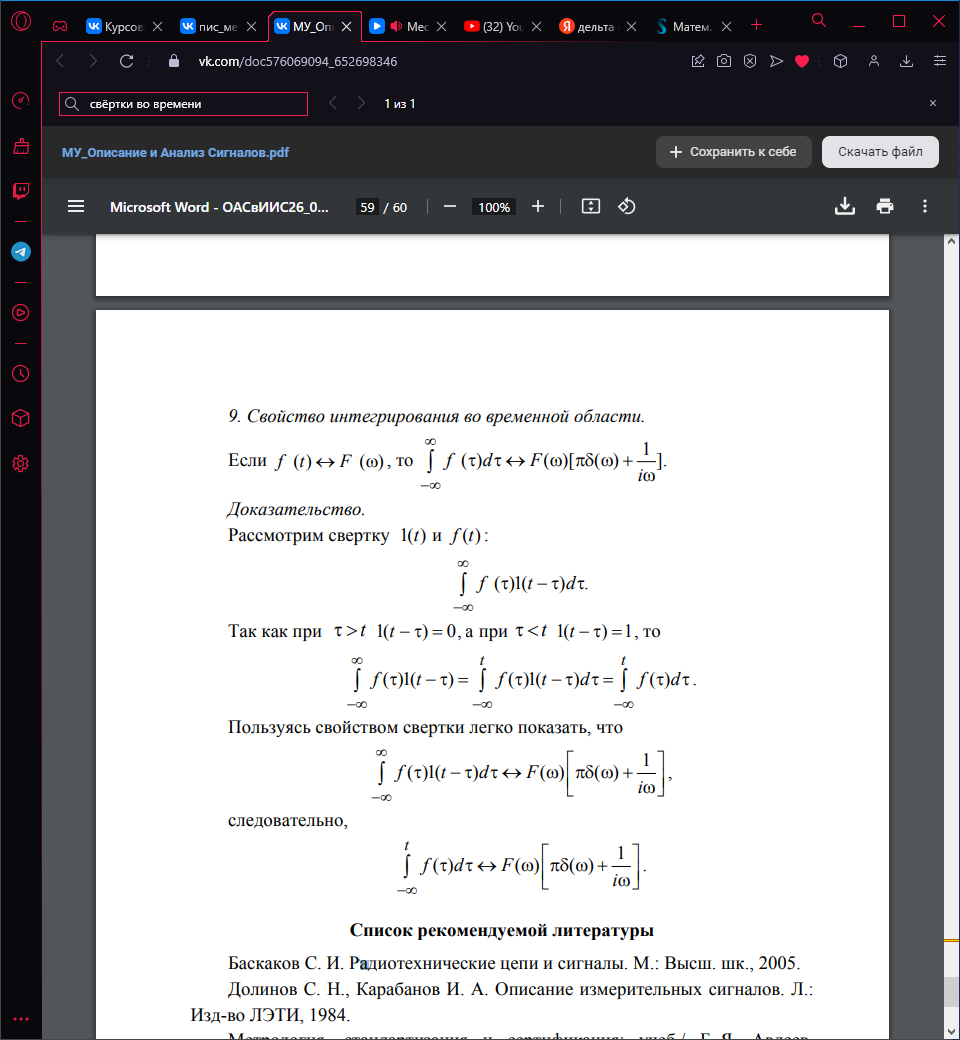
Так как при t: 1(t ) 0, а при t: 1(t ) 1, то
Пользуясь свойством свертки легко показать, что
следовательно,
26. Спектральная плотность энергии и мощности сигналов.
Спектральная плотность - функция, описывающая распределение энергии (мощности) сигнала в зависимости от частоты, то есть энергия (мощность), приходящаяся на единичный интервал частоты.
Энергия сигнала


Имеем
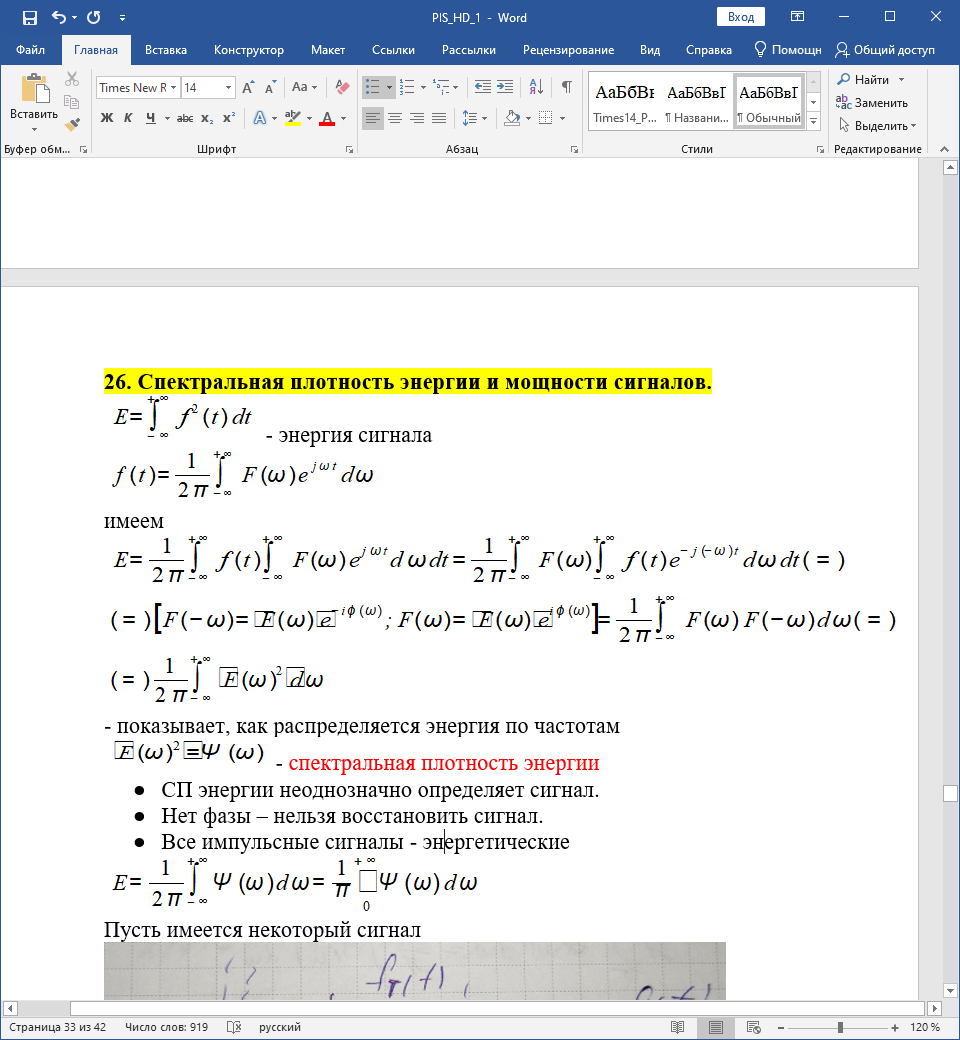
- выражение показывает, как распределяется энергия по частотам
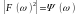
- спектральная плотность энергии
СП энергии неоднозначно определяет сигнал.
Нет фазы – нельзя восстановить сигнал.
Все импульсные сигналы - энергетические
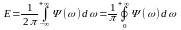
Пусть имеется некоторый сигнал
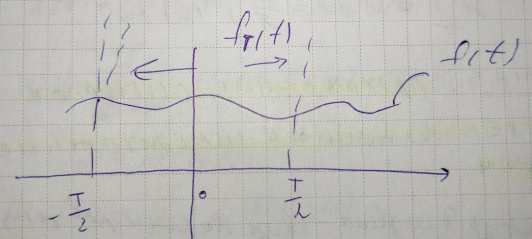
для fт(t):

На ∞ E = ∞. Для таких сигналов определяют среднюю мощность.
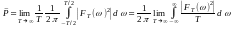
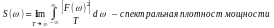
- определяет распределение мощности по частотам
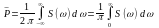
27. Частотные характеристики линейных измерительных цепей.
Для линейных цепей выполняется принцип суперпозиции:
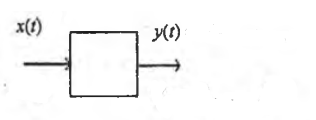
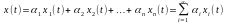
выходной сигнал можно представить в виде:
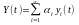
это справедливо только для линейных цепей.
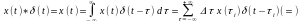
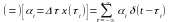

где h(t) – реакция цепи на δ – функцию

H(ω) – частотные характеристики – показывает насколько хорошо или плохо передается сигнал