13. Комплексный спектр сигналов.

Комплексный спектр сигнала можно получить из действительного спектра и формулы Эйлера:

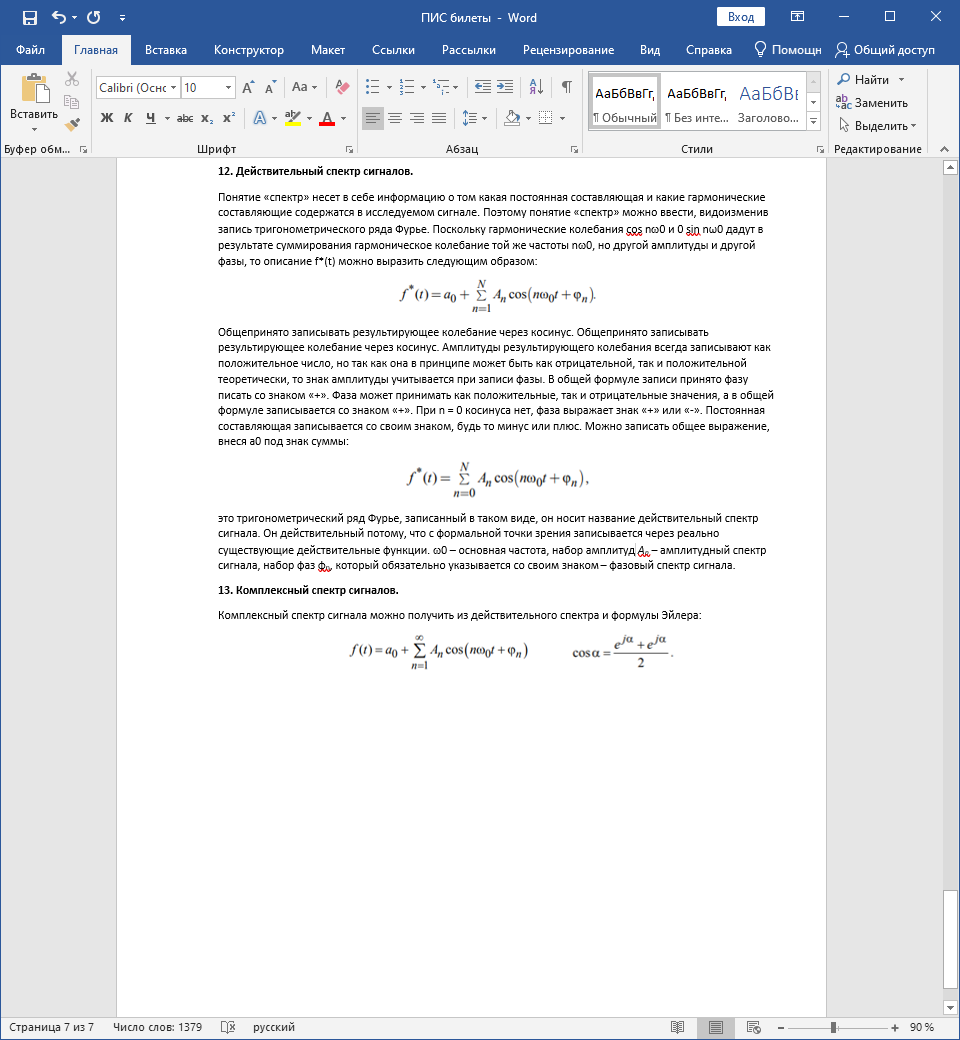
Получим:

Функцию f(t) можно предоставить в виде ряда, который называют экспоненциальным рядом Фурье:

где Fn – коэффициенты разложения, являются комплексными числами и определяются из выражения

для фазы вектора выполняется условие n  n, таким образом, комплексные числа Fn и Fn на положительных и отрицательных частотах отличаются только знаком фазы и являются комплексно-сопряженными числами.

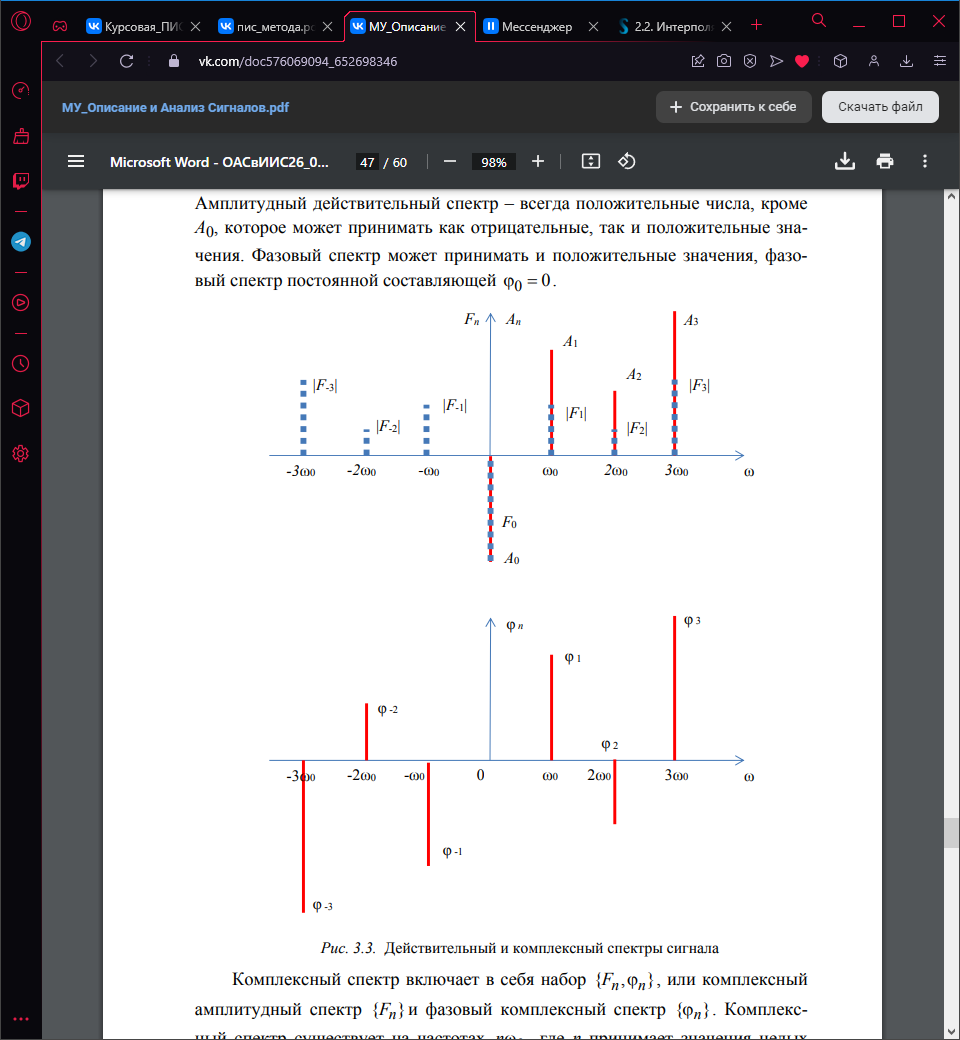
Комплексный спектр включает в себя набор {Fn,n}, или комплексный амплитудный спектр { Fn } и фазовый комплексный спектр {n }. Комплексный спектр существует на частотах nω0, где n принимает значения целых чисел от  до   . Амплитудный комплексный спектр в два раза меньше, чем амплитуда действительного спектра, кроме постоянной составляющей |F0|= A0, значения амплитуд комплексного спектра на отрицательных частотах, равно значению амплитуд комплексного спектра на положительных частотах |Fn|=|F-n|.

Амплитудный комплексный спектр {Fn} является четной функцией. Фазы комплексного спектра на положительных частотах равны значению фаз действительного спектра, фазы комплексного спектра на отрицательных частотах равны по модулю и противоположны по знаку фазам комплексного спектра на положительных частотах. Комплексный фазовый спектр {n} является нечетной функцией.

14. Спектральная плотность непериодических сигналов.

Спектральная плотность – это непрерывная функция частоты (спектр будет сплошной, а не линейный):

где F() – непрерывная функция, которая называется спектральной плотностью.

Таким образом:

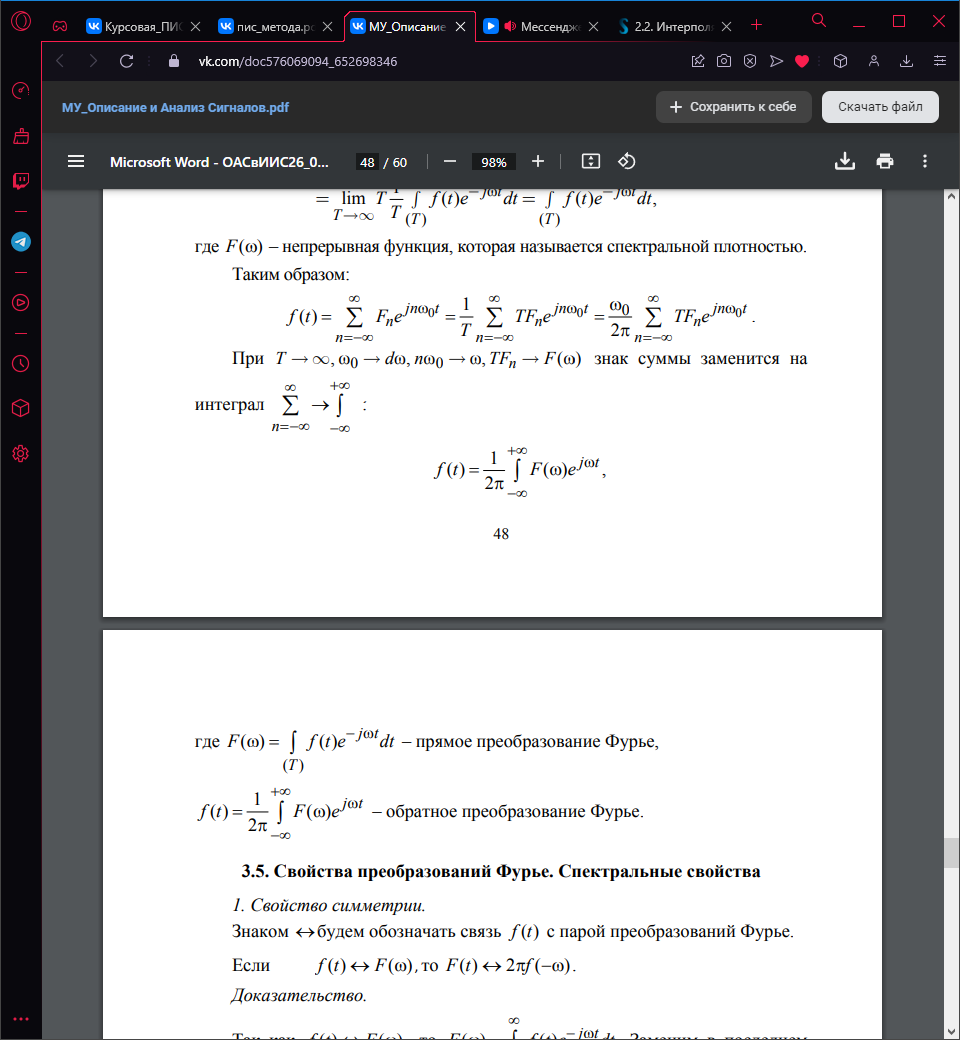
При T∞, ω0dω, nω0ω, TFnF(ω) знак суммы заменится на интеграл

15. Свойство симметрии.

Знаком будем обозначать связь f (t) с парой преобразований Фурье.

Если f (t)  F (), то F(t)  2f() .

Доказательство: так как f (t)  F (), то

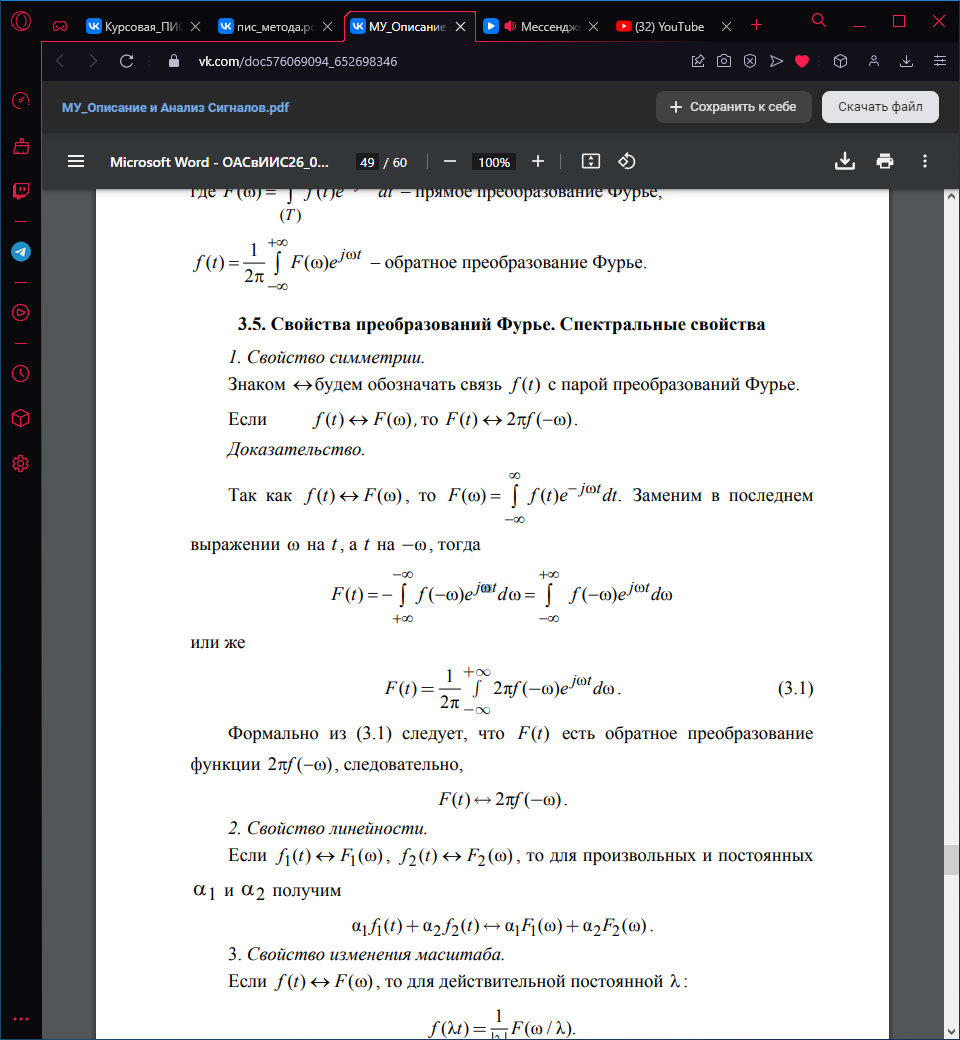
Заменим в последнем выражении  на t, а t на -ω, тогда

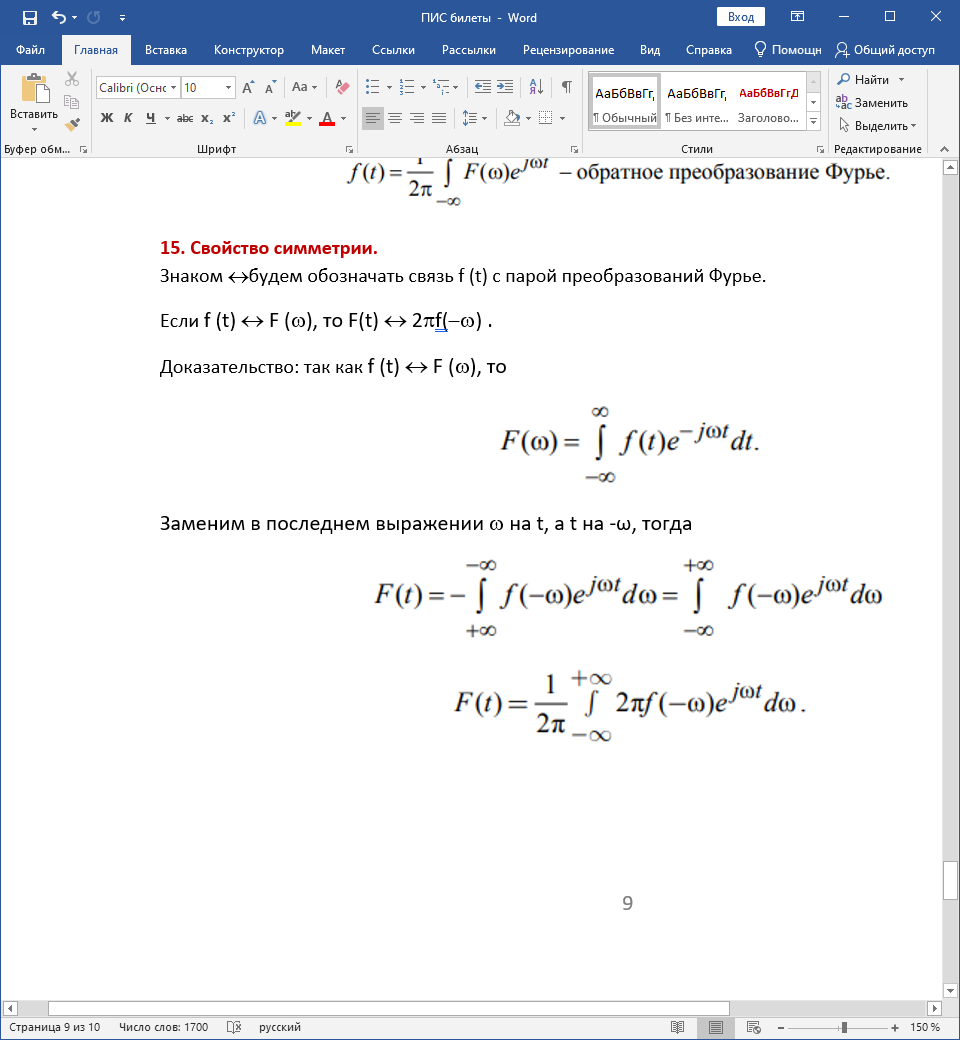
Формально из этого следует, что F(t) есть обратное преобразование функции 2f (), следовательно,

16. Дельта-импульс. Его свойства. Спектральная плотность Дельта-импульса.

ẟ функция позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.

Прямое преобразование Фурье:

Это спектральная плотность дельта функции

19. Свойство изменения масштаба.

Если f (t)  F (), то для действительной постоянной  :

Доказательство: пусть   0. Так как

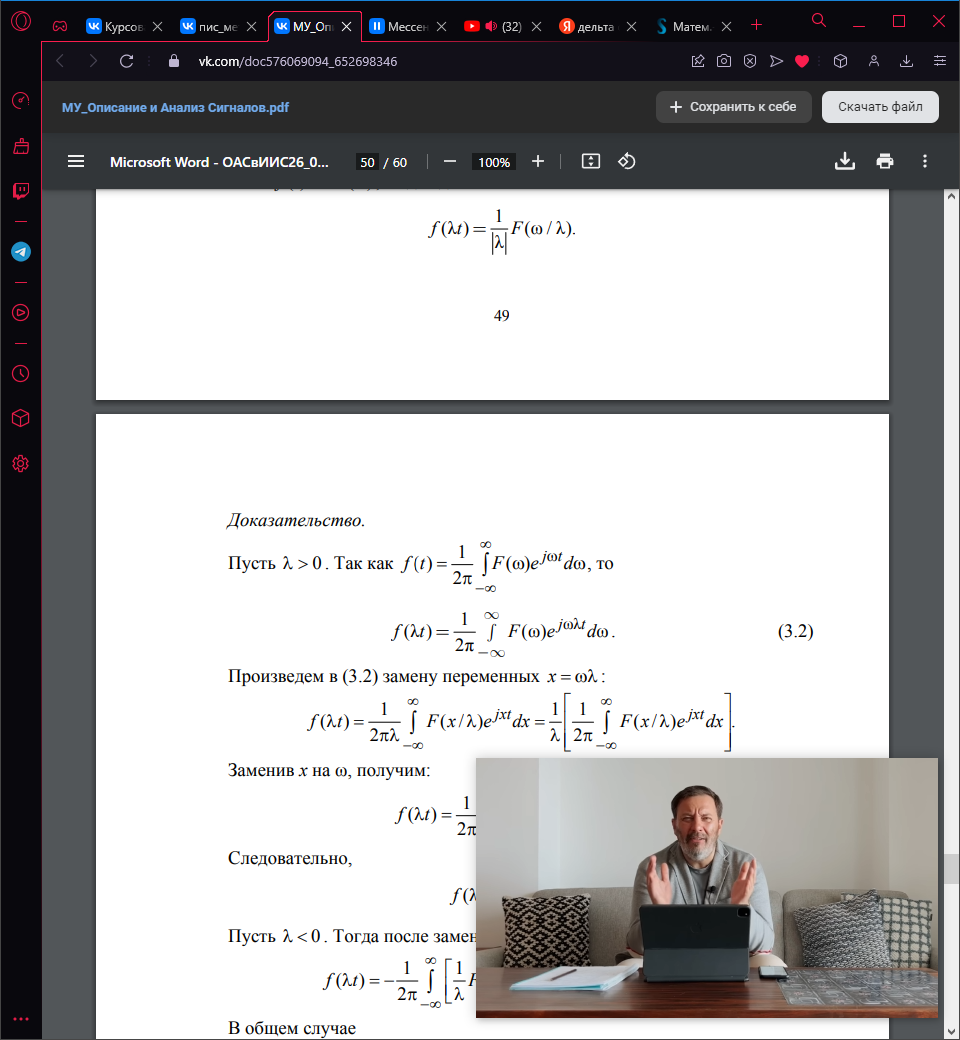
Произведем замену переменных x   :

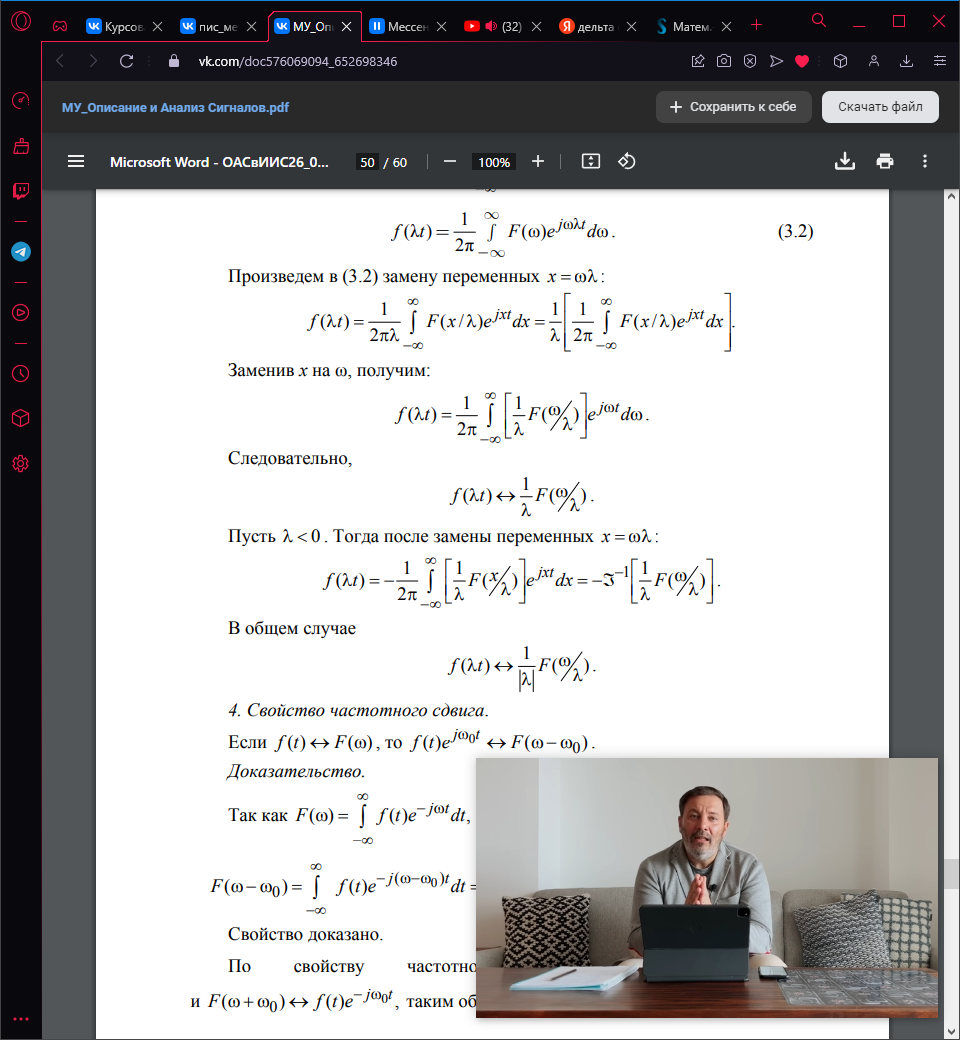
Заменив x на ω, получим:

Следовательно,

Пусть   0. Тогда после замены переменных x   :

В общем случае

Таким образом, при изменении масштаба времени в  раз масштаб частот для спектра меняется в 1/[| раз. Значит, увеличение длительности сигнала приводит к сужению его спектра. И наоборот, чем короче сигнал по времени, тем шире его спектр.

20. Свойство временного и частотного сдвига. Теорема о модуляции.

Свойство временного сдвига (теорема запаздывания)

Если f (t)  F (), то f (t-t0)  F () e^-jwt0, где t0 – время запаздывания.

Доказательство: пусть f (t)  F (), тогда

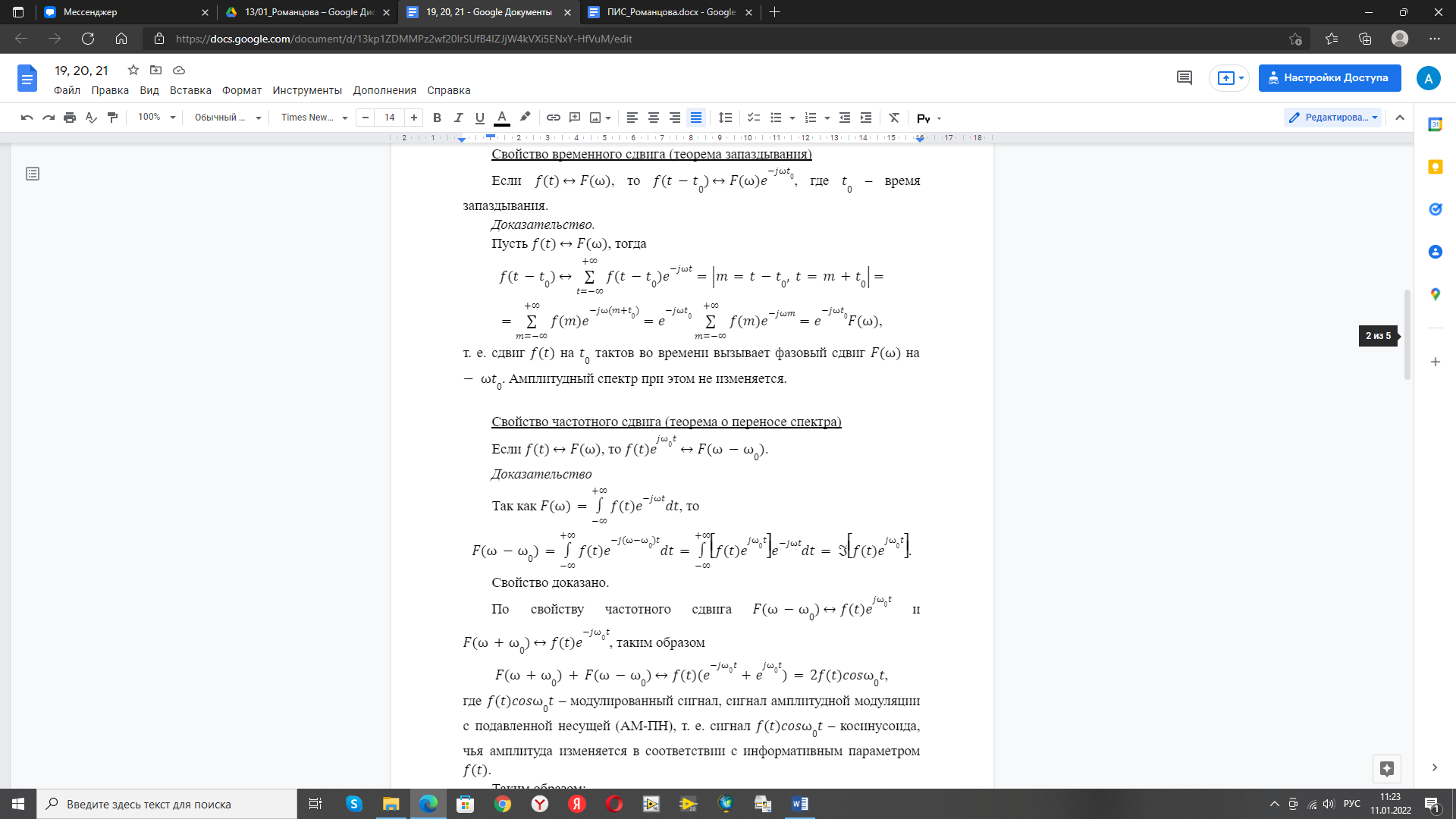
т.е. сдвиг f(t) на t0 тактов во времени вызывает фазовый сдвиг F () на -t0. Амплитудный спектр при этом не изменяется.

Свойство частотного сдвига (теорема о переносе спектра)

Если f (t)  F (), то f (t) e^jw0t  F ( - 0).

Доказательство: так как

Свойство доказано.

По свойству частотного сдвига

где f(t)cos w0t – модулированный сигнал, сигнал амплитудной модуляции с подавленной несущей (АМ-ПН), т.е. сигнал f(t)cos w0t - косинусоида, чья амплитуда изменяется в соответствии с информативным параметром f(t).

Таким образом:

Теорема о модуляции: модулированному сигналу f(t)cos w0t соответствует спектральная плотность

Данная теорема позволяет анализировать спектры модулированных сигналов.