3. Описание сигналов по Тейлору. Оценка погрешности.

Для описания сигнала по Тейлору полиномом n-го порядка необходимо знать в одной точке значения сигнала и его производных до n-го порядка включительно.

В качестве такой точке на интервале [-1, 1] берется точка

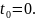
Формула Тейлора:(вместо х поставить t)

где 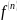- n-я производная сигнала.

Следует обратить внимание, что формула Тейлора очень хорошо описывает сигнал вблизи узловой точки. Однако о удалением от этой точки погрешность резко возрастает.

Эмпирическая погрешность, находится из графиков для i-го полинома:

Оценка максимальной погрешности для i-го полинома:

где – модуль-максимум ( )-й производной сигнала на рассматриваемом интервале

4. Оценка погрешности полиномиального описания сигналов в равномерной метрике.

Эмпирическая погрешность, находится из графиков для i-го полинома:

Оценка максимальной погрешности для i-го полинома:

где – модуль-максимум ( )-й производной сигнала на рассматриваемом интервале

5. Полиномы Чебышева. Свойство старших коэффициентов и свойство корней.

Полиномы Чебышева были найдены как результат решения системы дифференциальных уравнений. Алгебраическая форма записи полиномов Чебышева выглядит следующим образом:

Целое число n – определяет порядок полинома Чебышева. По формуле для n = 0, 1, 2, … возможно получить в общем виде полиномы Чебышева 0, 1, 2… порядков, причем формула рассматривается на интервале t [1;1] и все свойства полиномов Чебышева справедливы на данном интервале.

Тригонометрическая форма полинома Чебышева:

Рекуррентная формула:

Свойство старших коэффициентов: старшие коэффициенты по порядкам от 0 можно записать как: 2⁰, 2¹, 2², 2³ … откуда следует общее правило, называемое свойством старшего коэффициента:

Возможно записать полином Чебышева с любым старшим коэффициентом. Полином Чебышева не изменит формы, изменится лишь его масштаб.

Полином Чебышева с произвольным an старшим коэффициентом:

Свойство корней: корни полиномов ищут, приравнивая полином к нулю и решая соответствующее уравнение. Полином степени n имеет n корней, при больших n решение уравнения, превращается в громоздкую и трудоемкую процедуру. Задача отыскания корней полинома Чебышева проста, если выразить полином Чебышева через переменную α и приравнять выражение к 0:

Точки обращения косинусоиды в ноль известны, полином Чебышева обращается в ноль, если:

Переменная t [1,1], таким образом, t  cos на этом диапазоне будет располагаться симметрично относительно нуля, косинус отрицательного и положительного значений одинаков, следовательно, корни полинома Чебышева слева и справа от нуля одни и те же. Полиномы Чебышева четного порядка всегда четные функции, полиномы Чебышева нечетного порядка всегда нечетные функции.

6. Полиномы Чебышева. Свойство экстремумов и фундаментальное свойство.

Свойство экстремумов: все экстремумы полиномов Чебышева равны по величине и последовательно чередуются по знаку.

Полиному Чебышева со старшим коэффициентом 2^n1 соответствуют экстремумы, равные  1; у полиномов Чебышева с единичным старшим коэффициентом экстремумы равны  1/2^n1

Экстремумы полинома Чебышева находят по следующей формуле:

Полином Чебышева n-го порядка имеет (n1) экстремум.

Фундаментальное свойство: полиномы Чебышева являются наименее уклоняющимися от 0, по сравнению с любым другим полиномом того же порядка и тем же старшим коэффициентом.