Оглавление

1. Описание сигналов по Лагранжу. Оценка погрешности. 1

2. Описание сигналов по Ньютону. Оценка погрешности. 2

3. Описание сигналов по Тейлору. Оценка погрешности. 3

4. Оценка погрешности полиномиального описания сигналов в равномерной метрике. 4

5. Полиномы Чебышева. Свойство старших коэффициентов и свойство корней. 4

6. Полиномы Чебышева. Свойство экстремумов и фундаментальное свойство. 5

7. Описание сигналов по Чебышеву. Погрешность описания. 5

9. Описание сигналов в среднеквадратической метрике. Ортогональные функции. 6

10. Погрешность описания сигналов ортогональными функциями. 7

11. Ортогональные функции Уолша. 8

12. Действительный спектр сигналов. 10

13. Комплексный спектр сигналов. 11

14. Спектральная плотность непериодических сигналов. 12

15. Свойство симметрии. 12

16. Дельта-импульс. Его свойства. Спектральная плотность Дельта-импульса. 13

19. Свойство изменения масштаба. 13

20. Свойство временного и частотного сдвига. Теорема о модуляции. 14

21. Свойство. Дифференцирования. 15

22. Свойство свёртки во времени. 16

23. Свёртка сигналов с предварительным дифференцированием. 16

24. Свойство свёртки по частоте. 17

25. Свойство интегрирования. 17

26. Спектральная плотность энергии и мощности сигналов. 18

27. Частотные характеристики линейных измерительных цепей. 19

28. Условия неискаженной передачи сигналов. 20

29. Методы нахождения частотных характеристик. 21

1. Описание сигналов по Лагранжу. Оценка погрешности.

Описание сигнала по Лагранжу осуществляется с помощью интерполяционного полинома Лагранжа (интерполяция позволяет узнать, какие значения принимает функция в точках, не являющихся ее узлами), который имеет вид:

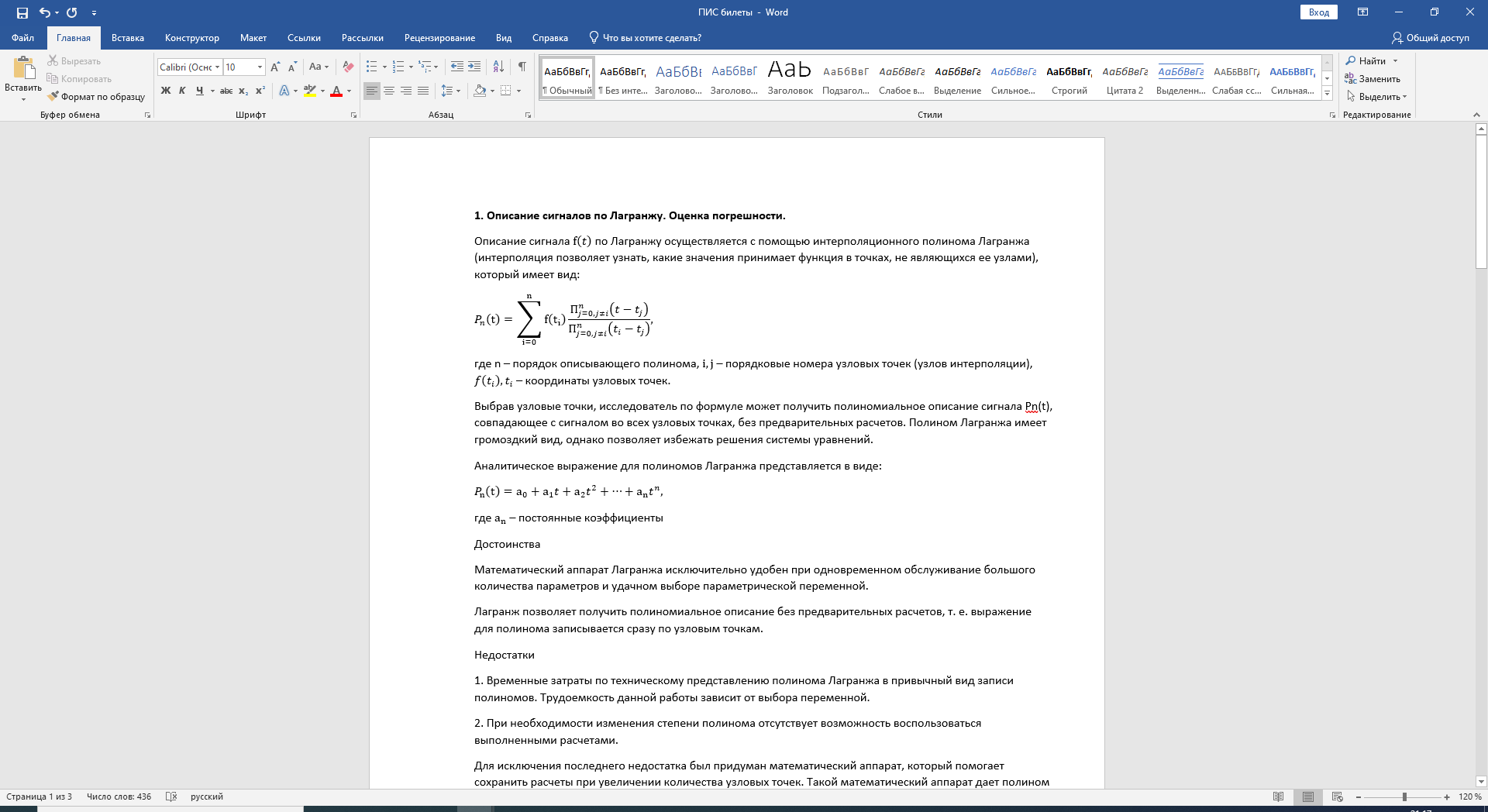
где n – порядок описывающего полинома, – порядковые номера узловых точек (узлов интерполяции), – координаты узловых точек.

Выбрав узловые точки, исследователь по формуле может получить полиномиальное описание сигнала Pn(t), совпадающее с сигналом во всех узловых точках, без предварительных расчетов. Полином Лагранжа имеет громоздкий вид, однако позволяет избежать решения системы уравнений.

Аналитическое выражение для полиномов Лагранжа представляется в виде:

где – постоянные коэффициенты

Достоинства

Математический аппарат Лагранжа исключительно удобен при одновременном обслуживание большого количества параметров и удачном выборе параметрической переменной.

Лагранж позволяет получить полиномиальное описание без предварительных расчетов, т. е. выражение для полинома записывается сразу по узловым точкам.

Недостатки

1. Временные затраты по техническому представлению полинома Лагранжа в привычный вид записи полиномов. Трудоемкость данной работы зависит от выбора переменной.

2. При необходимости изменения степени полинома отсутствует возможность воспользоваться выполненными расчетами.

Для исключения последнего недостатка был придуман математический аппарат, который помогает сохранить расчеты при увеличении количества узловых точек. Такой математический аппарат дает полином под названием «полином Ньютона».

Полиномы:

Эмпирическая погрешность, находится из графиков для i-го полинома:

Оценка максимальной погрешности для i-го полинома:

где – модуль-максимум ( )-й производной сигнала на рассматриваемом интервале

2. Описание сигналов по Ньютону. Оценка погрешности.

Полином Ньютона в отличие от полинома Лагранжа требует некоторых предварительных расчетов. В общем виде полином Ньютона записывается следующим образом:

Для нахождения описания сигналов при помощи полинома Ньютона необходимо знать координаты узловых точек. Для определения коэффициентов B требуется произвести элементарные расчеты.

Поиск коэффициентов при использовании таблицы происходит сверху вниз и слева направо. Полином Ньютона, который находится по данной схеме, носит название «нисходящий полином Ньютона».

Полином Ньютона, в отличие от полинома Лагранжа, создает возможность сохранить расчеты при переходе от полинома более низкого порядка к порядку выше. Недостаток полинома Ньютона – необходимость предварительных расчетов.

В практических расчетах при описании сигналов степенными полиномами стараются обойтись наиболее низкой степенью полинома, но такое описание может привести к большой погрешности описания. При увеличении степени полинома появляется дополнительная узловая точка. При использовании полинома Ньютона появление новой узловой точки не приводит к необходимости пересчитывать заново все коэффициенты формулы, к сумме добавляется еще одно слагаемое.

Эмпирическая погрешность, находится из графиков для i-го полинома:

Оценка максимальной погрешности для i-го полинома:

где – модуль-максимум ( )-й производной сигнала на рассматриваемом интервале