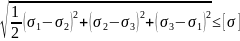- •Первая практическая задача
- •Вторая практическая задача
- •Список теоретических вопросов к/р лекц.
- •Что спросит на защите курсовой?
- •В методе сил объяснить как нашли по этому методу неизвестные. Спрашивать будет компоненты уравнения.
- •В методе начальных параметров будет спрашивать про компоненты уравнений и как применяли.
- •Некоторые термины из лекционной контрольной!. Подготовка к курсовой работе
Список теоретических вопросов к/р лекц.
Хрупкость - свойство материала разрушаться при небольшой (преимущественно упругой) деформации под действием напряжений, средний уровень которых ниже предела текучести. Образование хрупкой трещины и развитие процесса хрупкого разрушения связано с образованием малых зон пластической деформации .
Пластичность -механическое свойство материалов под влиянием внешней нагрузки изменять форму и размер, а после того как нагрузка перестает действовать — сохранять ее в измененном виде.
Прочность конструкции – свойство конструкции сопротивляться разрушению (разделению на части) под действием внешних нагрузок.
Жесткость конструкции – способность конструкции сопротивляться образованию деформации, не превышающих допустимых значений.
Деформация тела – изменение формы и размеров конструкции или ее элементов в результате внешнего воздействия.
В
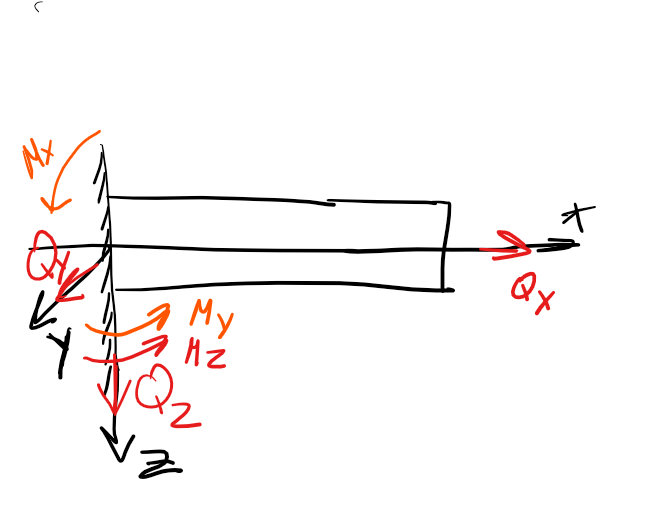 нутренняя
сила (или второе название внутренний
силовой фактор). Силы отвечают за
перемещение.
нутренняя
сила (или второе название внутренний
силовой фактор). Силы отвечают за
перемещение.
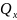 -
продольная сила.
-
продольная сила.
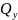 -
поперечная сила.
-
поперечная сила.
Моменты отвечают
за вращение тела:
-
поперечная сила.
-
поперечная сила.
Моменты отвечают
за вращение тела:
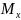 -крутящий
момент.
-крутящий
момент.
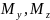 -
изгибающие моменты. (на рисунки к примеру
Mx вращается вокруг оси
x).
-
изгибающие моменты. (на рисунки к примеру
Mx вращается вокруг оси
x).
Г
 лавные
напряжения.
При растяжении сжатия
-
лавные
напряжения.
При растяжении сжатия
-
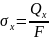 Напряжение
в теле находится в прямой зависимости
от внутренней величины
Напряжение
в теле находится в прямой зависимости
от внутренней величины
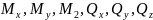 …. Зависит какой тип деформации стоит
в задаче. Еще зависит от геометрии тела
и свойств материала. Соответственно
чем толще тело, тем сложнее разломить.
Вектор
напряжений можно разложить на проекции.
На рисунке нормаль к данной площадке
ось X. Поэтому
…. Зависит какой тип деформации стоит
в задаче. Еще зависит от геометрии тела
и свойств материала. Соответственно
чем толще тело, тем сложнее разломить.
Вектор
напряжений можно разложить на проекции.
На рисунке нормаль к данной площадке
ось X. Поэтому
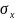 будет называться нормальным напряжением,
а остальные будут касаться -
будет называться нормальным напряжением,
а остальные будут касаться -
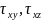 –
касательные.
Рассмотрим ситуацию,
когда ось y смотрит на
нас. Тогда будет
–
касательные.
Рассмотрим ситуацию,
когда ось y смотрит на
нас. Тогда будет
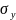 – нормальные. Остальные аналогично
касательные.
Немного про тензор
немного: по главной диагонали идут
нормальные напряжения. Главное
напряжение – это нормальные напряжение,
которые максимальны. Будет максимальным
когда вектор ляжет с осью. Всего
существует три главных напряжения.
Первое напряжение по первой оси. Если
для первого рисунка касательное
напряжение равно 0, то
– нормальные. Остальные аналогично
касательные.
Немного про тензор
немного: по главной диагонали идут
нормальные напряжения. Главное
напряжение – это нормальные напряжение,
которые максимальны. Будет максимальным
когда вектор ляжет с осью. Всего
существует три главных напряжения.
Первое напряжение по первой оси. Если
для первого рисунка касательное
напряжение равно 0, то
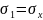 .
Для второго если касательные равны 0,
то
.
Для второго если касательные равны 0,
то
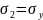 .
.


 Схематизация закрепления.
Реакция
опоры – запрет на перемещение на
вращение тела.
Жесткая заделка:
Шарнирно-неподвижное(или
подвижное) закрепление:
Схематизация закрепления.
Реакция
опоры – запрет на перемещение на
вращение тела.
Жесткая заделка:
Шарнирно-неподвижное(или
подвижное) закрепление:

Правило знаков для сил и для моментов. Если проекция силы на какую-то определённую ось направлена в противоположную сторону, чем на ось на которую направлена проекция данная сила будет отрицательна, а если проекция силы будет совпадать с проекцией, то данная сила положительна – Патрина Т.А. Правило: Если внешняя нормаль к поперечному сечению стержня совпадает с положительным направлением оси x, силы положительны, если совпадают по направлению с соответствующими осями координат; Моменты положительны, если создают вращение против часовой стрелки при взгляде с положительного конца соответствующей оси.
Физический смысл коэффициента Пуассона . Коэффициент Пуассона – это отношение относительного удлинения в поперечном к относительному удлинению в продольном. Коэффициент Пуассона для всех материалов лежит в пределах от 0 до 0,5 и зависит только от свойств самого материала.
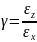


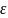 – понимать что за напряжение и как
направлены.
Относительное удлинение
показывается разницу между удлинением
и первоначальном длинной.
– понимать что за напряжение и как
направлены.
Относительное удлинение
показывается разницу между удлинением
и первоначальном длинной.
Закон парности касательных напряжений. На двух взаимно перпендикулярных площадках касательные напряжения, перпендикулярные к линии пересечения площадок, равны между собой:
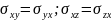 . Это свойство называется свойством
парности касательных напряжений. Таким
образом, тензор напряжений имеет всего
6 независимых компонентов.
. Это свойство называется свойством
парности касательных напряжений. Таким
образом, тензор напряжений имеет всего
6 независимых компонентов.Теорема Кастилиана: Рисунок и как применять. Когда нужно найти прогиб допустим в стержне. После того как стала действовать нагрузка стержень прогнулся. Соответственно на сколько произошел прогиб по Y например. Позволяет найти теорема Кастилиано.
 Формулировка:
Производная потенциальной энергии
деформации тела по одной из независимых
внешних сил равна перемещению
соответствующей силы. Обобщенное
перемещение при изгибе находится по
формуле:
Формулировка:
Производная потенциальной энергии
деформации тела по одной из независимых
внешних сил равна перемещению
соответствующей силы. Обобщенное
перемещение при изгибе находится по
формуле:
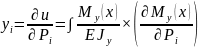 При
поперечном изгибе My. При
растяжение сжатие заменяется на N(x).
Если было бы кручение то потенциальная
энергия раскрывается через полярный
момент, а не осевой.
Если у нас угол
поворота:
При
поперечном изгибе My. При
растяжение сжатие заменяется на N(x).
Если было бы кручение то потенциальная
энергия раскрывается через полярный
момент, а не осевой.
Если у нас угол
поворота:
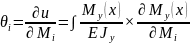 Пример:
Пример:
 По
теореме сечение делаем справо налево(
с конца) и длинна отсеченной части равна
x. Для силы положительной
силы P плечо отрицательно
.
По
теореме сечение делаем справо налево(
с конца) и длинна отсеченной части равна
x. Для силы положительной
силы P плечо отрицательно
.
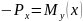 .
.
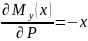 (взяли производную от прошлого
выражения)
Идем с конца. Сила P
действует в координате 0 и до силы L.
Интеграл соответственно расставляем.
В итоге:
(взяли производную от прошлого
выражения)
Идем с конца. Сила P
действует в координате 0 и до силы L.
Интеграл соответственно расставляем.
В итоге:
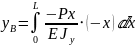 Пример
2:
Пример
2:

Формула Максвелла Мора. Перемещение от приложенной силы равно : Нужно найти интеграл ( в той точки где действует сила и до конца стержня), и сечение делается всегда с конца стержня.
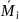 -
момент вызванный единичной обобщенной
силой.
M- момент от
заданной нагрузки. (момент от силы
P).
(В этой формуле
используется замена переменных.
Закрепления стержня заменяем на
обобщенные силы и черта обозначает,
что сила равна единицы.)
-
момент вызванный единичной обобщенной
силой.
M- момент от
заданной нагрузки. (момент от силы
P).
(В этой формуле
используется замена переменных.
Закрепления стержня заменяем на
обобщенные силы и черта обозначает,
что сила равна единицы.)
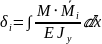
Формула Журавского. (написано в Поперечном изгибе) В произвольной точке прямоугольного поперечного сечения балки касательное напряжение определяют по формуле Д. И. Журавского:

Принцип Сен-Венана. Если размеры области приложения внешней нагрузки невелики по сравнению с размерами поперечного сечения стержня, то в сечениях, достаточно удаленных от места приложения нагрузки, напряжения и деформации мало зависят от способа реализации нагрузки.
Знание трех типов деформации тела: Знать какие внутренние силы возникают. Растяжение и сжатие: Будет только одна сила - , а
 .
Кручение:
Будет Mx, а
.
Кручение:
Будет Mx, а
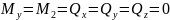 Поперечный
изгиб – Действует сила
Поперечный
изгиб – Действует сила
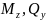 , а остальные 4 равны 0.
Сложное
сопротивление – Могут быть
, а остальные 4 равны 0.
Сложное
сопротивление – Могут быть
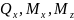 ,
а то есть все возможные внутренние
силы.
Эпюры – график зависимости
величины внутренний силы от значения
величины длины стержня.
,
а то есть все возможные внутренние
силы.
Эпюры – график зависимости
величины внутренний силы от значения
величины длины стержня.
 Закон
Гука линейного типа.
Закон говорит
нам о том, что связи между деформацией
и напряжением одинаковы в любой точки
и главные оси деформации совпадают с
нормалям к главным площадкам.
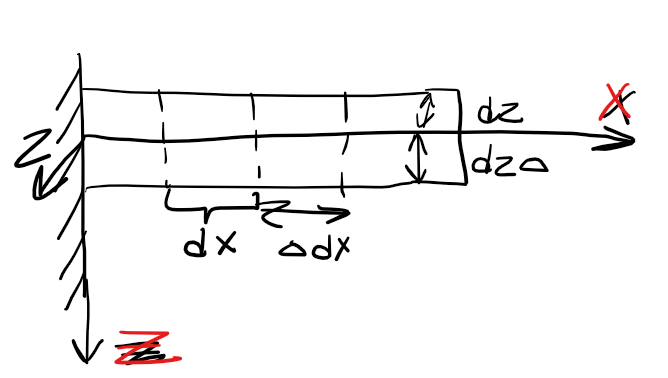
Рассмотрим
с вами стержнем и его деформацию с
течением времени. Имеем участок dx
и растянулось на участок
Закон
Гука линейного типа.
Закон говорит
нам о том, что связи между деформацией
и напряжением одинаковы в любой точки
и главные оси деформации совпадают с
нормалям к главным площадкам.
Рассмотрим
с вами стержнем и его деформацию с
течением времени. Имеем участок dx
и растянулось на участок
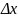 . Ось x проходим через
центр тяжести. Выделим участок в
поперечном сечении dz, то
допустим с течением времени произошла
деформация
. Ось x проходим через
центр тяжести. Выделим участок в
поперечном сечении dz, то
допустим с течением времени произошла
деформация
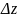 .
В поперечном это называется относительное
удлинение
.
В поперечном это называется относительное
удлинение
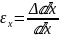 .
А
если рассмотрим в поперечном
.
А
если рассмотрим в поперечном
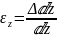 .
Если
линейная деформация, то
.
Если
линейная деформация, то
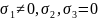 ,
то в данном случае Закон Гука будет
равен
,
то в данном случае Закон Гука будет
равен
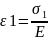 ,
где E-модуль упругости.
Соответственно так как сигма 2 и 3 по
нулям, то
,
где E-модуль упругости.
Соответственно так как сигма 2 и 3 по
нулям, то
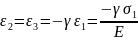 .
.
Закон Гука деформированного типа(объемного деформированного состояния тела). Объяснить физические величины. Если идет объемная деформация в главных осях, то будет система уравнений.
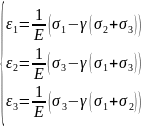 Если
нужно расписать закон через произвольные
оси, то соответственно будет
аналогично:
Если
нужно расписать закон через произвольные
оси, то соответственно будет
аналогично:
 Зависимость
между модулем сдвига и модулем упругости:
Зависимость
между модулем сдвига и модулем упругости:
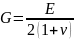
Четыре теории прочности. (знать применение) 1 теория прочности: Говорит о том что в хрупких материал возникает в точке, когда наибольшее нормально напряжение является растягивающим . Соответственно идет по оси X, ибо растягивающим, а так как нормальное, то возникает
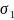 .
Данную теорию можно применять если
идет только растяжение. Еще применяют
коэффициент запас, для устранения
погрешностей, чтобы границу уменьшить
и возник запас по теории прочности.
.
Данную теорию можно применять если
идет только растяжение. Еще применяют
коэффициент запас, для устранения
погрешностей, чтобы границу уменьшить
и возник запас по теории прочности.
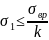 2
теория прочности: Хрупкое
разрушение в точке возможно когда
относительная деформация по первой
оси, первая главная деформация, не
достигает критического значения. Тут
применяется закон гука для объемного
тела.
2
теория прочности: Хрупкое
разрушение в точке возможно когда
относительная деформация по первой
оси, первая главная деформация, не
достигает критического значения. Тут
применяется закон гука для объемного
тела.
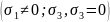 Для
деформации.
Для
деформации.
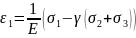 Если
мы перейдем к напряжениям, а не к
деформации, тогда оно не должно превышать
критическое (из таблицы берется).Берется
при сжатии и растяжении, когда у нас
хрупкий материал:
Если
мы перейдем к напряжениям, а не к
деформации, тогда оно не должно превышать
критическое (из таблицы берется).Берется
при сжатии и растяжении, когда у нас
хрупкий материал:
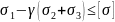 3
теория прочности: Деформация тела
происходит пластичная. Она находится
через касательные напряжения. Пластичная
деформация возникает, когда максимальное
касательное напряжение достигает
определенного для данного материала
критического значения. Максимальное
касательное напряжение находится как:
3
теория прочности: Деформация тела
происходит пластичная. Она находится
через касательные напряжения. Пластичная
деформация возникает, когда максимальное
касательное напряжение достигает
определенного для данного материала
критического значения. Максимальное
касательное напряжение находится как:
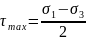 .
.
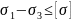 ,
где
,
где
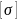 критичное значение (предел текучести
деленное на k).
4 теория
прочности: Здесь мы находим удельную
энергию деформации тела и она не должна
превышать максимального размера.
Пластичная деформации возникает,
когда достигает некоторого предела
удельная энергия формоизменения. Причем
вклад в энергию деформации вносит
только та часть работы, которая связана
с упругой деформацией (остальная
превращается в теплоту).
критичное значение (предел текучести
деленное на k).
4 теория
прочности: Здесь мы находим удельную
энергию деформации тела и она не должна
превышать максимального размера.
Пластичная деформации возникает,
когда достигает некоторого предела
удельная энергия формоизменения. Причем
вклад в энергию деформации вносит
только та часть работы, которая связана
с упругой деформацией (остальная
превращается в теплоту).