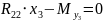Делал: Кашин Даниил Практическая часть
T е н з о р — это форма записи, выражающая линейное преобразование трехмерного пространства в некоторой систе¬ме координат. Число компонент тензора определяет его ранг.
Напряженное состояние в окрестности тела характеризуется девятью составляющими напряжений, которые обычно записывают в виде тензора напряжений и называется компонентами тензора.
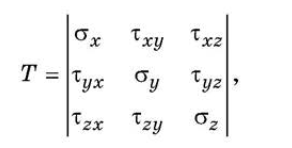
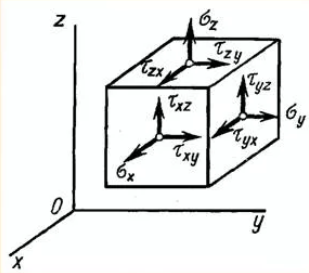
Первые буквы индексов касательных напряжений показывают направление действия, а вторые — направление нормали к той площадке, на которой они действуют. Напряжения, возникающие в направлении, перпендикулярном к сечению, называют нормальными, обозначаются σ. Напряжения, возникающие в плоскости сечения, называют касательными, обозначаются τ. Площадка, на которой касательные напряжения равны нулю, называется главной площадкой.
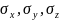-Главные(нормальные) напряжения.
- Касательные напряжения.
К примеру есть нормальное и касательное для поперечного изгиба.
-Осевой
момент.
В произвольной точке прямоугольного поперечного сечения балки касательное напряжение определяют по формуле Д. И. Журавского:
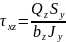,Sy-
Статический момент:определяется как
площадь отсеченной части, умноженная
на расстояние между центром тяжести
всего сечения и центром тяжести отсеченной
части сечения. b - ширина поперечного
сечения на рассматриваемой высоте
поперечного сечения.
Виды напряжений при деформации
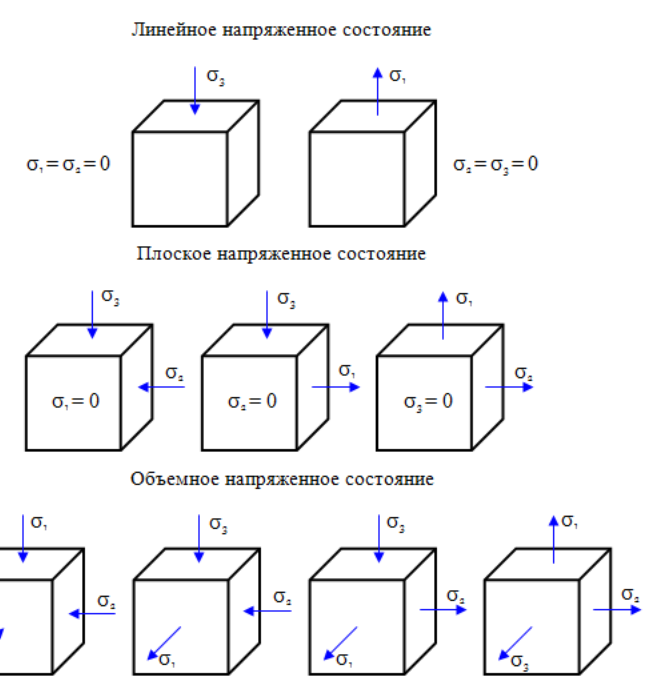Виды
напряженного состояния: линейное
напряженное состояние (два главных
напряжения равны нулю), плоское
напряженное состояние (одно из
главных напряжений равно нулю) и объемное
напряженное состояние (все главные
напряжения не равны нулю).
Примечание: Все что приведено выше – это была общая теория. На контрольной она будет давать тензор и ваша задача будет найти похожий, а после следовать конкретной теории.
Первая практическая задача
Растяжение и Сжатие
Нормальные и касательные, когда сечение
происходит под некоторым углом:
,
;
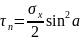Нормальное
напряжение зависит от внутренний силы
и площади:
Формула по нахождению главных напряжений (возникают тогда когда сигма икс становится максимальным и касательные равны 0)
,
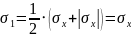Кручение
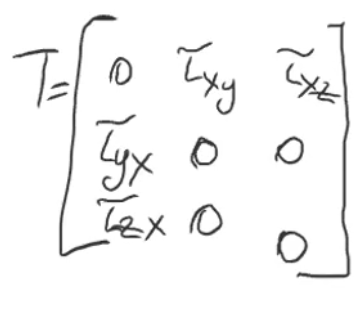Так
как Mx изгибающий момент
вращается, то он касается площадки, а
значит нормальных компонентов нет.
Формулы
для касательных напряжений:
,
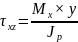
(Jp полярный момент). Не забываем про закон парности касательных напряжений (xy=yx,zx=xz).
Общее
касательное напряжение:
;
Полярный
момент для круга:
Формула
главных напряжений(взято из конспекта):
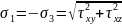
Поперечный изгиб
Н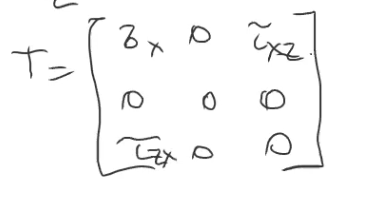
ормальное
напряжение:
, где Jy- осевой момент.
для круга к примеру.
Касательное
напряжение (фор-ла Журавского):
,Sy-
Статический момент: определяется как
площадь отсеченной части, умноженная
на расстояние между центром тяжести
всего сечения и центром тяжести отсеченной
части сечения. b - ширина поперечного
сечения на рассматриваемой высоте
поперечного сечения.
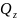– продольная сила.
Для сечения под углом альфа
Нормальное
напряжение:
Касательное
напряжение:
Формулы
главных напряжений:
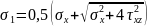
Формула
положения главных площадок: (угол б ищем
ибо он положение главных площадок)
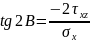
Вторая практическая задача
В этой задаче она дает расчетную схему на один из типов деформации: поперечный изгиб, кручение и растяжение или сжатие. Попросит написать одно уравнение. Либо уравнение сил либо уравнение моментов для определенного участка. Сечение также укажет с какой стороны делать (слева направо или справа налево).
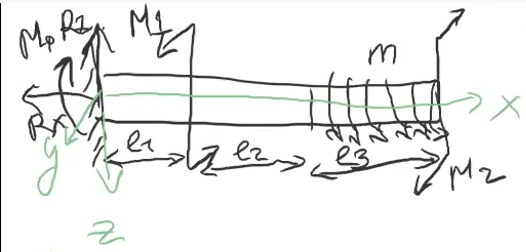
Кручение
1
этап Уравнение Равн-сия:
2 этап Уравнение Моментов: Вращение моментов можно понять, если посмотреть в какую сторону вращается момент в плоскости yz вокруг начал СК. My тогда по часовой, M1 против, M2 по часовой и чтобы сделать из m умножаем на расстояние l3 и вращается против часовой. Против часовой с плюсом , а если по то с минусом.
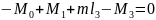
3 этап Метод сечений:
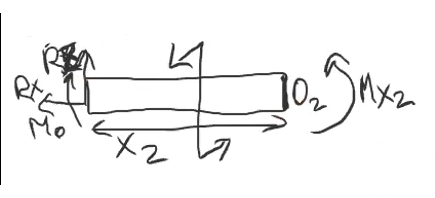
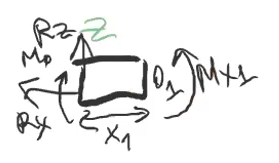Делая
сечение слева направо M2
не попадает на третьем участке, так как
делаем сечение на конце.
У-М:
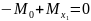
2
участок
У-М:
3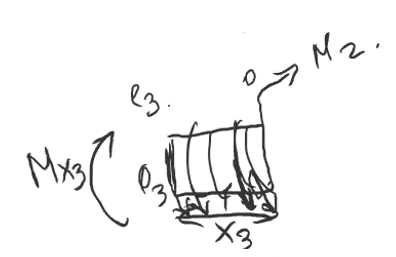
участок (сечение справа налево)
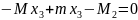
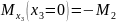
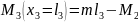
Растяжение и сжатие
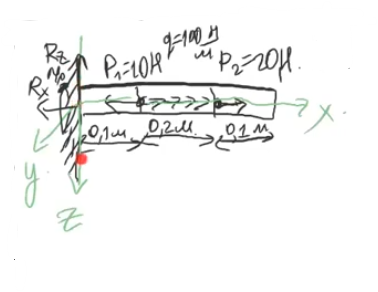1
этап – Уравнение Равновесий
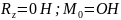(проекция на ось x=0)
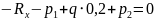
Метод сечений-2этап
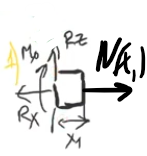1
участок:
N(xn)-Внутренняя сила.
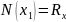
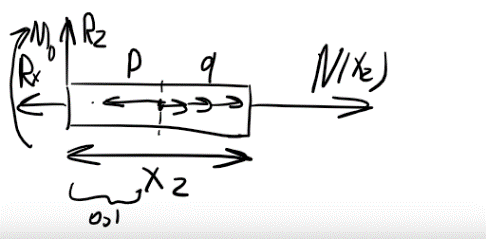2
участок
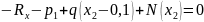
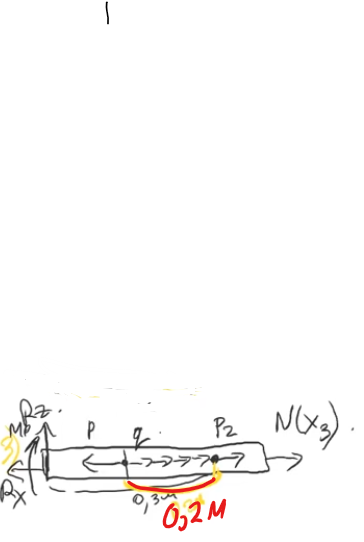3 участок
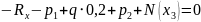
Сложное сопротивление – их 3 вида. Но Патрина разобрала некоторые.
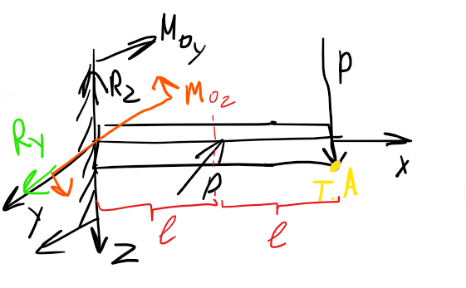Сложный
изгиб это изгиб в двух плоскостях :
вокруг оси Y
и оси Z.
(
)
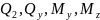1
этап – Уравнение равновесия для двух
плоск.:
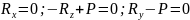
2
этап – Уравнение моментов отн.т.А для
двух плоск.:
3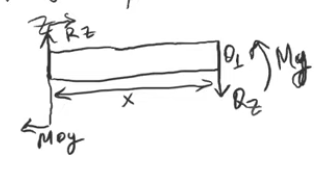
этап- Метод сечений
Б
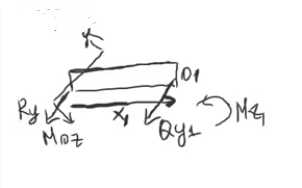удет
один участок в плоскости Z.
У-С:
У-М:
Отн.т.O1; Когда делаем
сечение слева направо, то плечи и
внутр.силы положительны.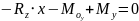
В
вертикальной плоскости будет 2 грузовых
участка.
У-С:
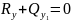У-М:
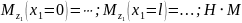
Сечением сделаем с конца и тогда внутренняя сила будет отрицательна У-С:
У-М:
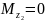
Изгиб с растяжением и сжатием (-)
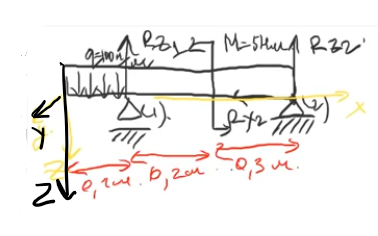Изгиб
с кручением (поперечный) – (Qz;
My);
1 этап - Уравнение равновесия:
Уравнение
моментов отн.1:
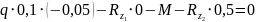
У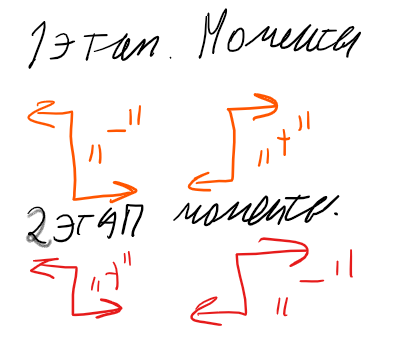
равнение
моментов отн.2:
;
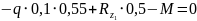Плечи относительно выбранной точки слева отрицательны, а справа положительны. Силы направленные вверх отрицательны, а вниз положительны.
2 этап:
1
)Уравнение
сил:
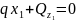
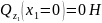
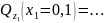У-М
(отн.места сечения): Плечи тоже положительны
при сечении слева направо.
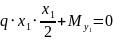
2)
У-С:
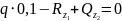У-М:
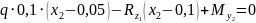
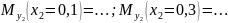3)
У-С: (Внутренние силы и плечи отрицательные,
ибо сечение справа налево)
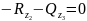У
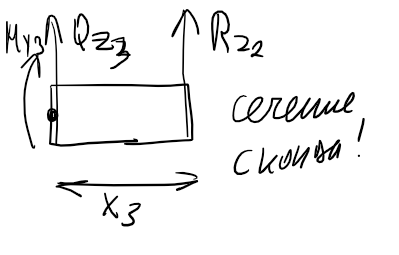-М:
