Medvedev_9587_TOE_LR_4

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №4

по дисциплине «Теоретические основы электротехники»

Тема: ИССЛЕДОВАНИЕ УСТАНОВИВШЕГОСЯ СИНУСОИДАЛЬНОГО РЕЖИМА В ПРОСТЫХ ЦЕПЯХ

Студент гр. 9587		Медведев Г.Н.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2021

Цель работы: практическое ознакомление с синусоидальными режимами в простых RL-, RC-и RLC-цепях.

Основные теоретические приложения

При анализе электрических цепей в установившемся синусоидальном режиме важно твердо усвоить амплитудные и фазовые соотношения между токами и напряжениями элементов цепи. Необходимо помнить, что ток в R-элементе совпадает по фазе с напряжением, ток в L-элементе отстает, а в C-элементе опережает напряжение на четверть периода (90°).

Следует учитывать, что комплексные сопротивления индуктивности и емкости есть функции частоты:

Функциями частоты являются, следовательно, и комплексные сопротивления RL- (рисунок 1, б), RC- (рисунок 1, а) и RLC-цепей (рисунок 1, в). Так, для RLC-цепи комплексное сопротивление

.

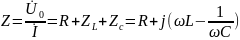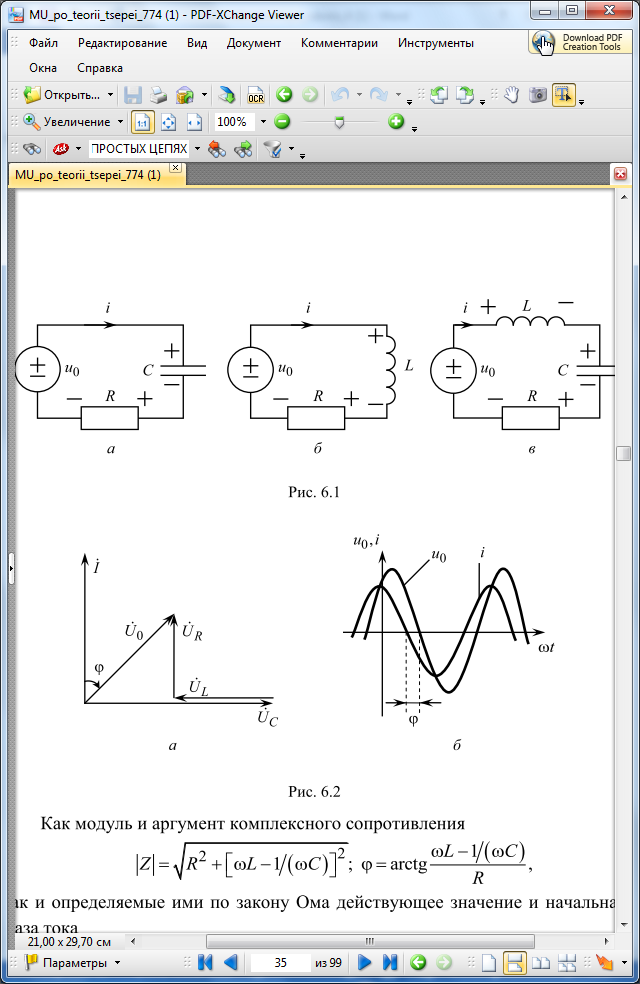
Рисунок 1 – схемы RL-, RC- и RLC-цепей

Реактивная составляющая этого сопротивления равна разности модулей индуктивного и емкостного сопротивлений и поэтому может принимать различные знаки: если она положительна, реакция цепи имеет индуктивный характер, если отрицательна–емкостный, если обращается в нуль (т.е. ), цепь будет находиться в состоянии резонанса.

Как модуль и аргумент комплексного сопротивления

так и определяемые ими по закону Ома действующее значение и начальная фаза тока

существенно зависят от соотношения значений индуктивного и емкостного сопротивлений.

Токи и напряжения цепи в установившемся синусоидальном режиме наглядно представляют с помощью ВД.

Протокол измерений

Таблица 1

Устанавливают		Измеряют					Вычисляют
№	f, кГц	I, мА	UR, В	UС, В	UL, В	φос	R, Ом	L, Гн	С, мкФ	φвд
1-RC	8	4,122	5,91	5,576	-	43,2	1430	-	0,015	43,5
2-RC	16	5,776	5,9	3,9	-	35,3	1020	-	0,015	33,5
3-RL	8	5,188	5,24	-	4,7	41,2	1010	0,020	-	41,5
4-RL	4	5,918	5,98	-	3,7	32	1010	0,024	-	31,8
5-RLC	8,24	6,268	6,66	8,143	8,249	0	1060	0,025	0,015
6-RLC	16,48	3,175	3,21	2,035	8,234	60	1010	0,025	0,015	62,5
7-RLC	4,12	3,2	3,25	8,213	2,099	61,3	1020	0,025	0,015	62

Обработка экспериментальных результатов

1. Исследование установившегося режима в RC -цепи

Соберем RC – цепь:

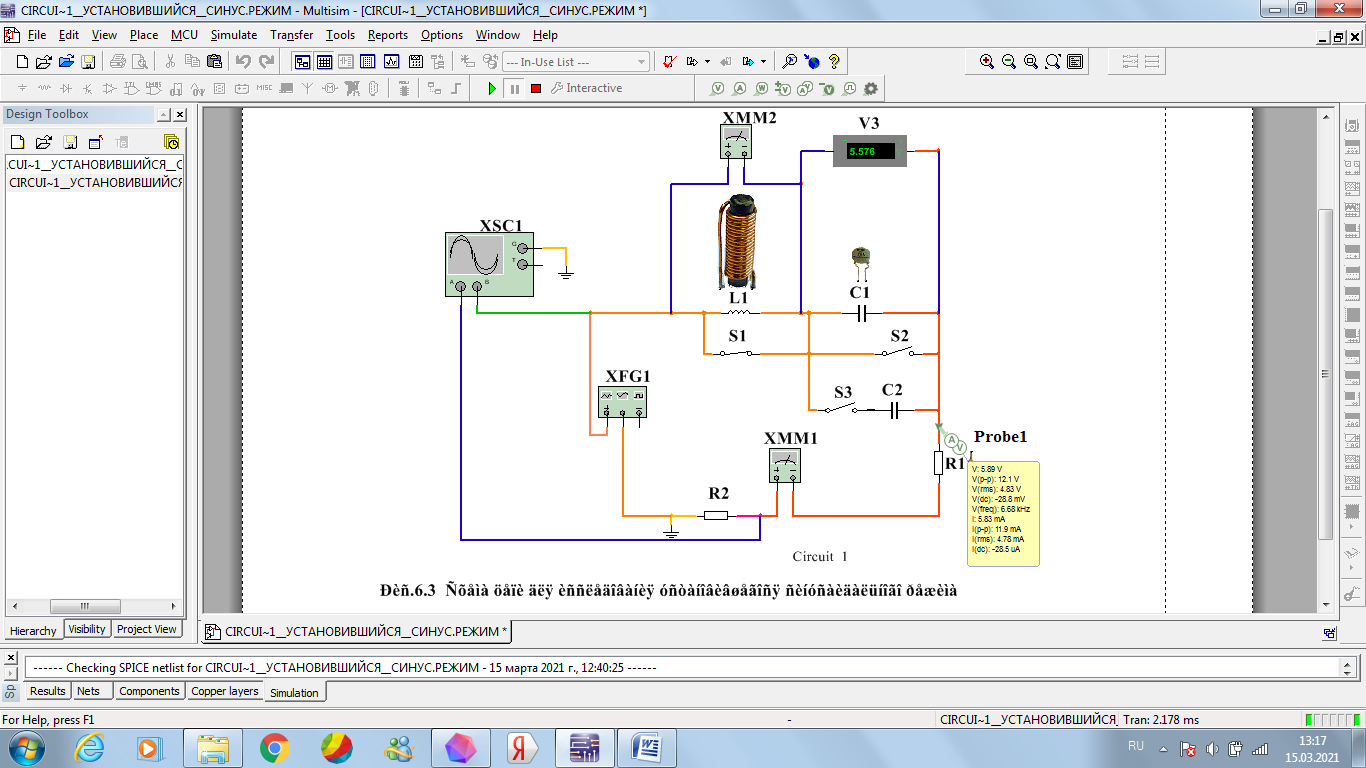
Рисунок 2 – схема RC – цепи

При 8 кГц:

Рисунок 3 – схема RC – цепи при 8 кГц

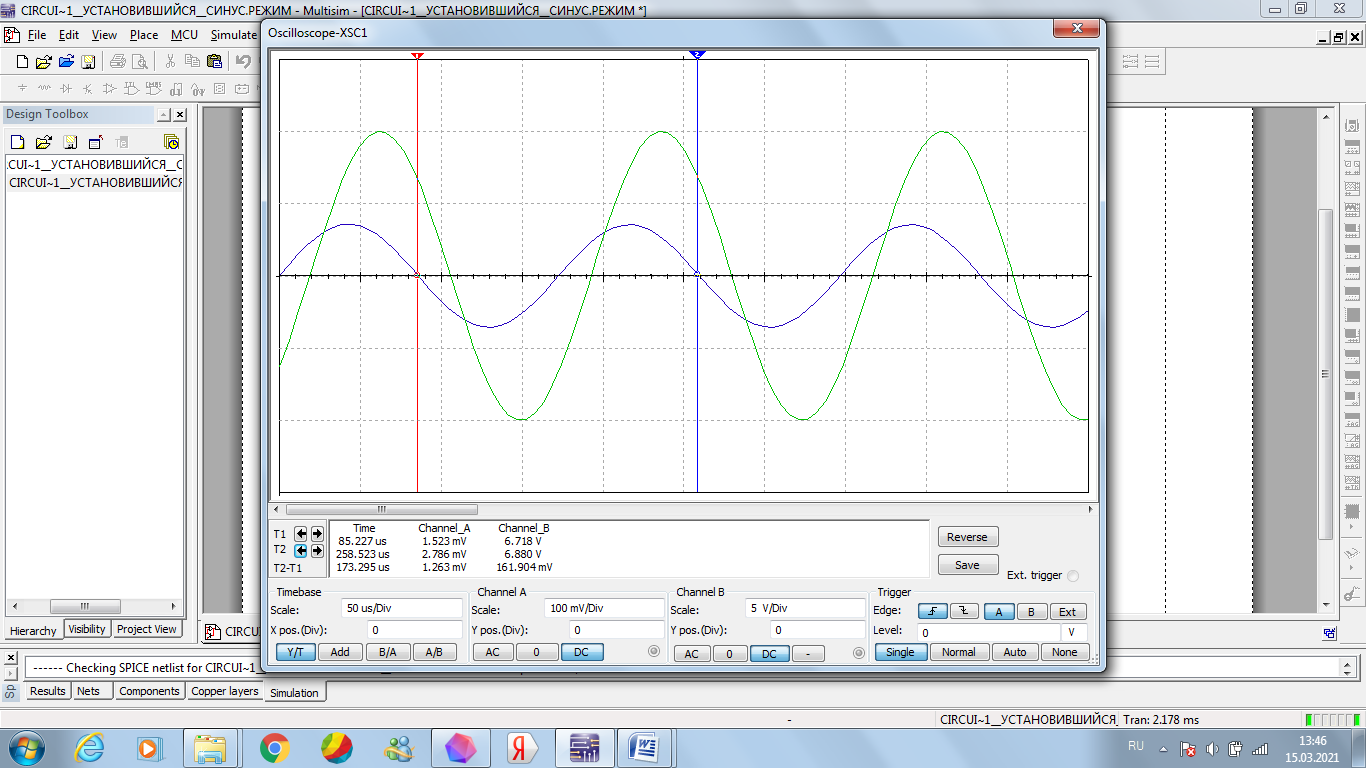
Рисунок 4 – осциллограмма входного напряжения и тока при 8 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

Рисунок 5 – векторная диаграмма тока и напряжений

Вычислим φос8:

Вычислим R, |Z_C|, C:

R = U_R/I=

|Z_C| = U_C/I=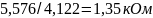

С =

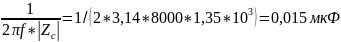
Занесем полученные значения в таблицу 1.

При 16 кГц:

Рисунок 6 – схема RC – цепи при 16 кГц

Рисунок 7 – осциллограмма входного напряжения и тока при 16 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

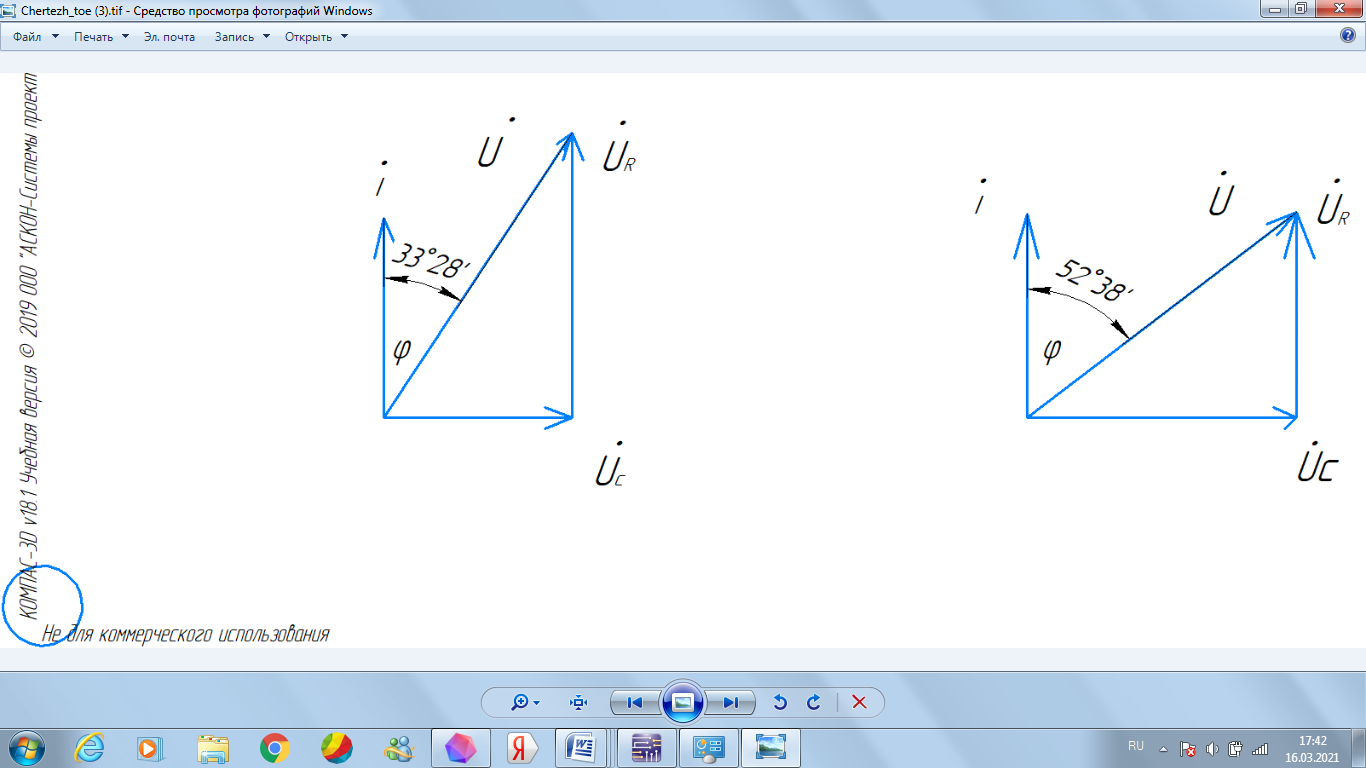
Рисунок 8– векторная диаграмма тока и напряжений

Вычислим φос16:

Вычислим R, |Z_C|, C:

R = U_R/I=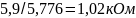

|Z_C| = U_C/I=

С =

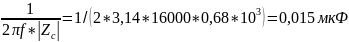
Занесем полученные значения в таблицу 1.

2. Исследование установившегося режима в RL –цепи

Рисунок 9 – схема RL – цепи

При 8 кГц:

Рисунок 10 – схема RL – цепи при 8 кГц

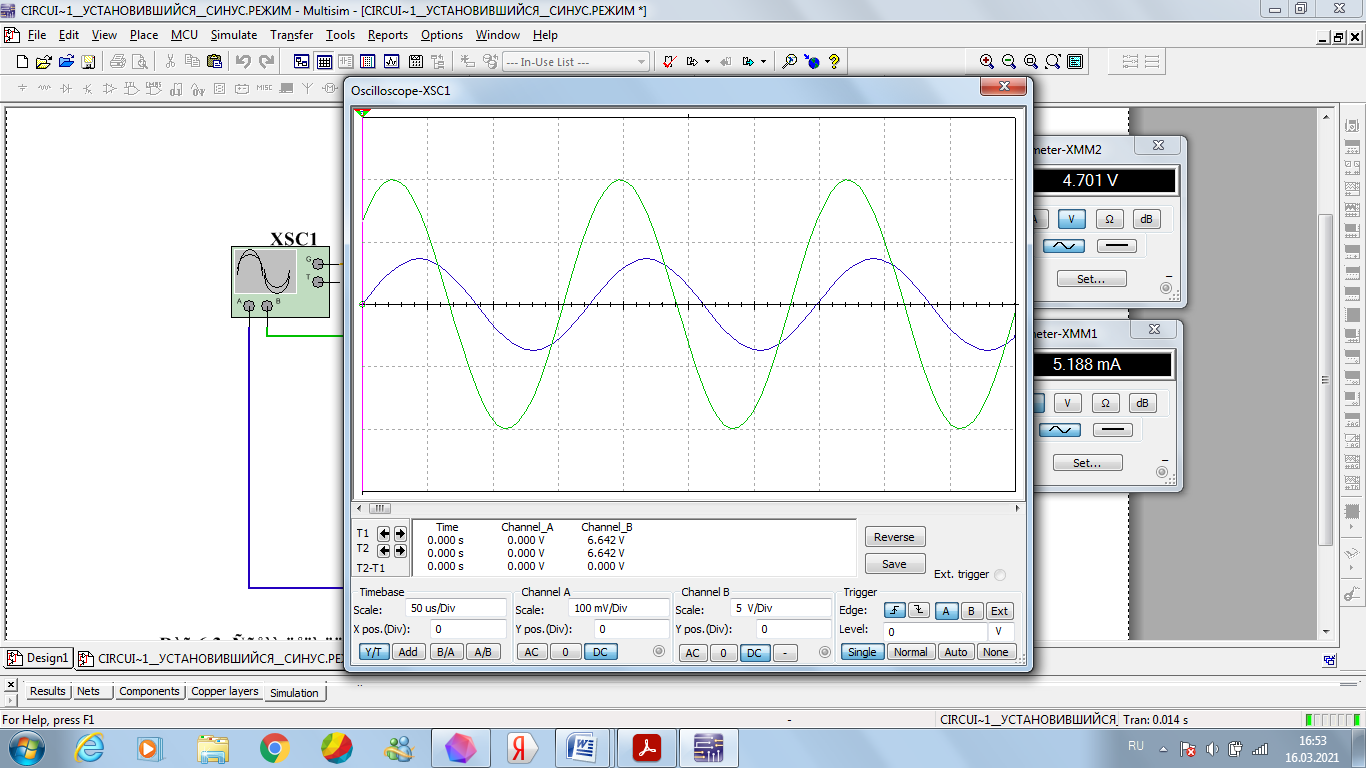
Рисунок 11 – осциллограмма входного напряжения и тока при 8 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

Рисунок 12– векторная диаграмма тока и напряжений

Вычислим φос8:

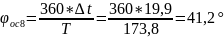
Вычислим R, |Z_L|, L:

R = U_R/I=

|Z_L| = U_L/I=

Занесем полученные значения в таблицу 1.

При 4 кГц:

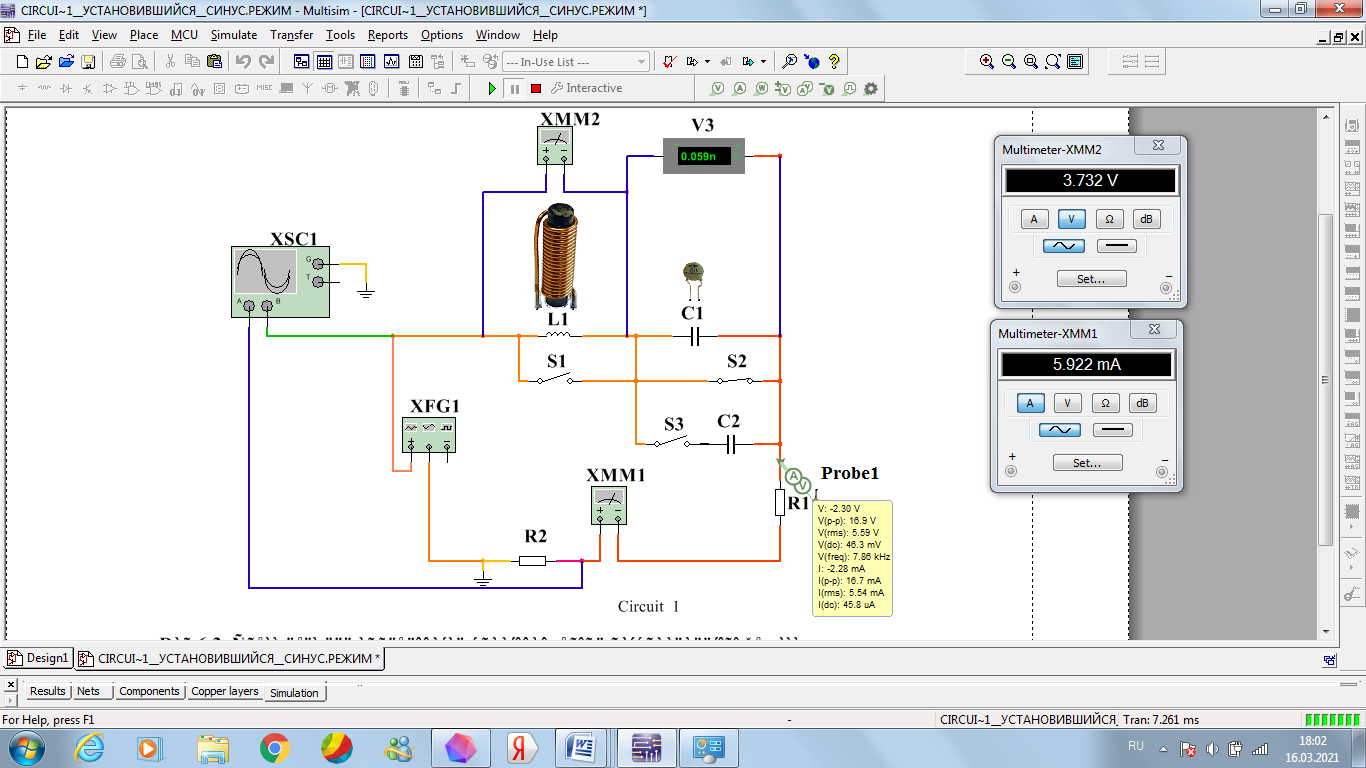
Рисунок 13 – схема RL – цепи при 4 кГц

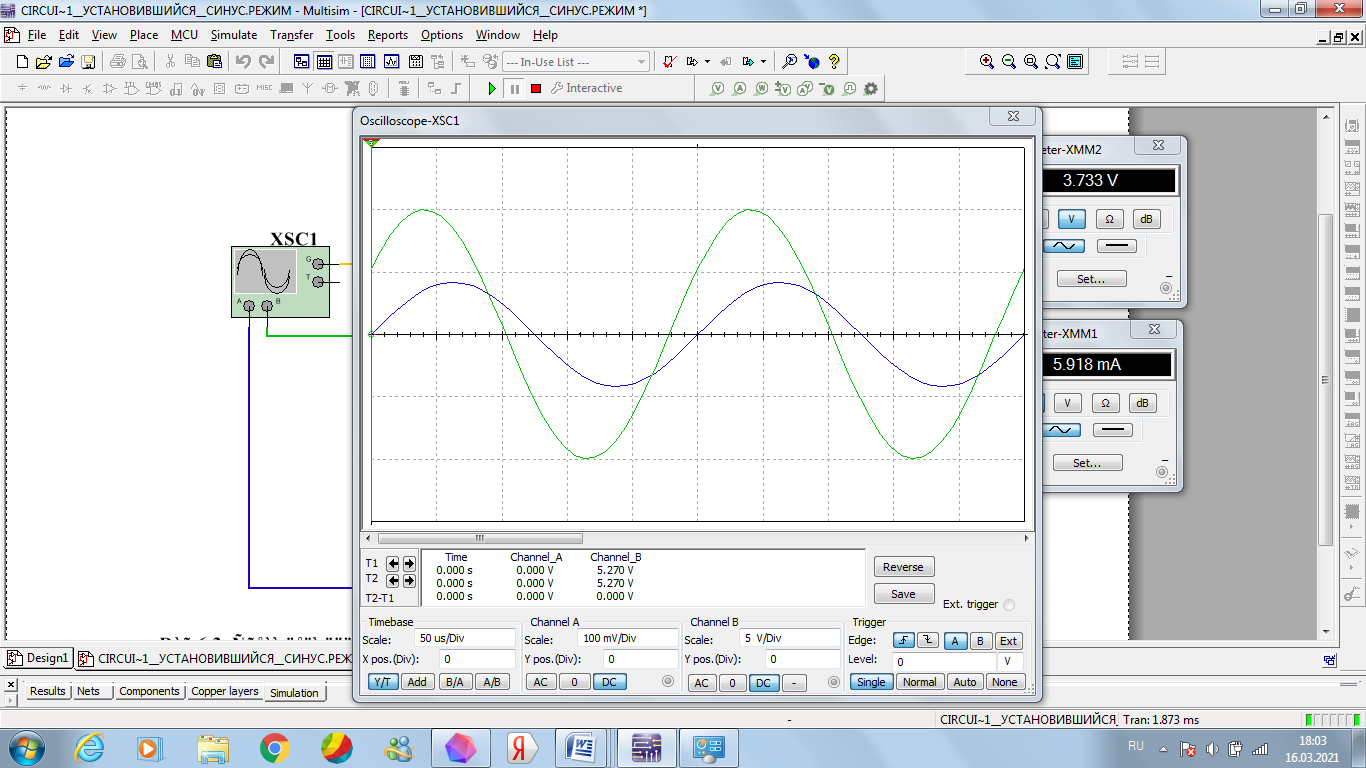
Рисунок 14 – осциллограмма входного напряжения и тока при 4 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

Рисунок 15– векторная диаграмма тока и напряжений

Вычислим φос4:

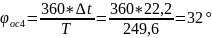
Вычислим R, |Z_L|, L:

R = U_R/I=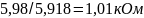

|Z_L| = U_L/I=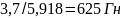

Занесем полученные значения в таблицу 1.

3. Исследование установившегося режима в RLC –цепи

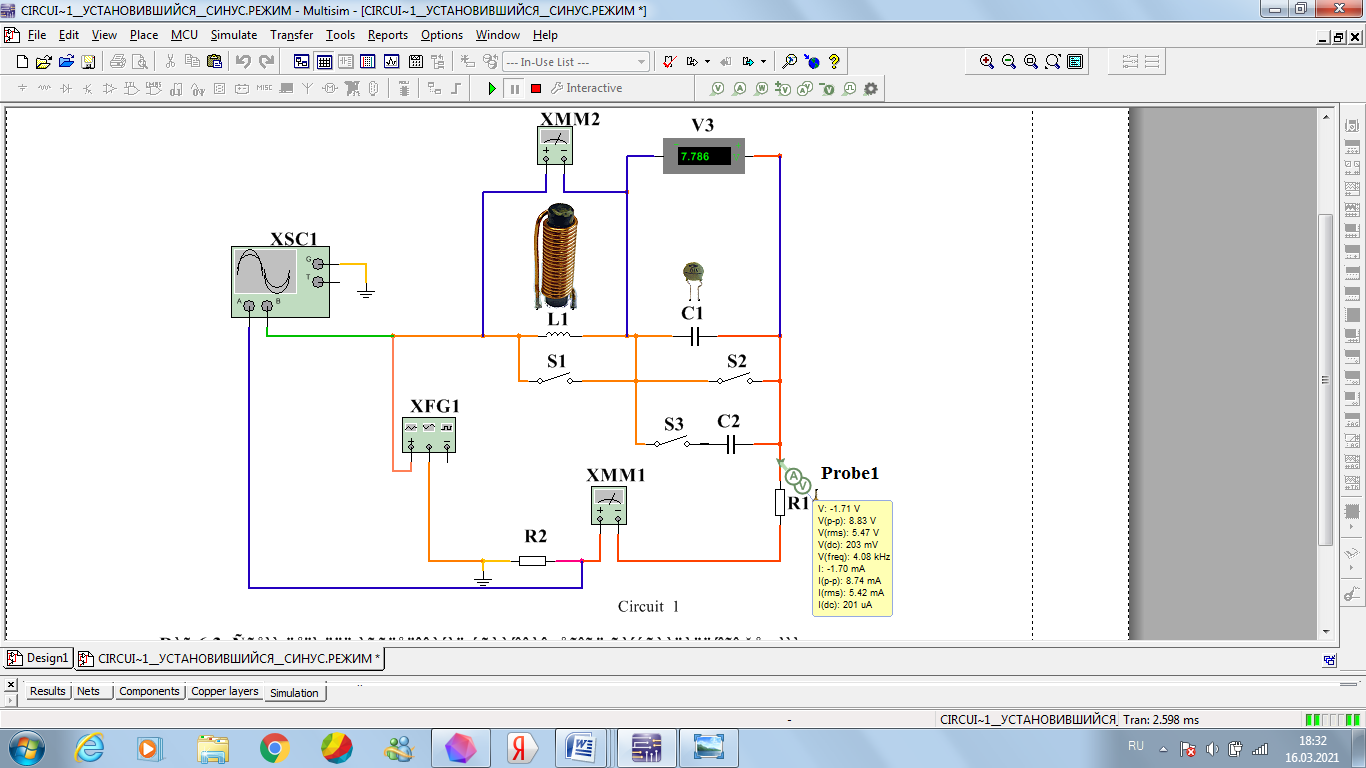
Рисунок 16 – схема RLC – цепи

Найдем резонансную частоту с помощью фигуры Лиссажу:

Рисунок 17 – фигура Лиссажу

Резонансная частота .

При 8,24 кГц:

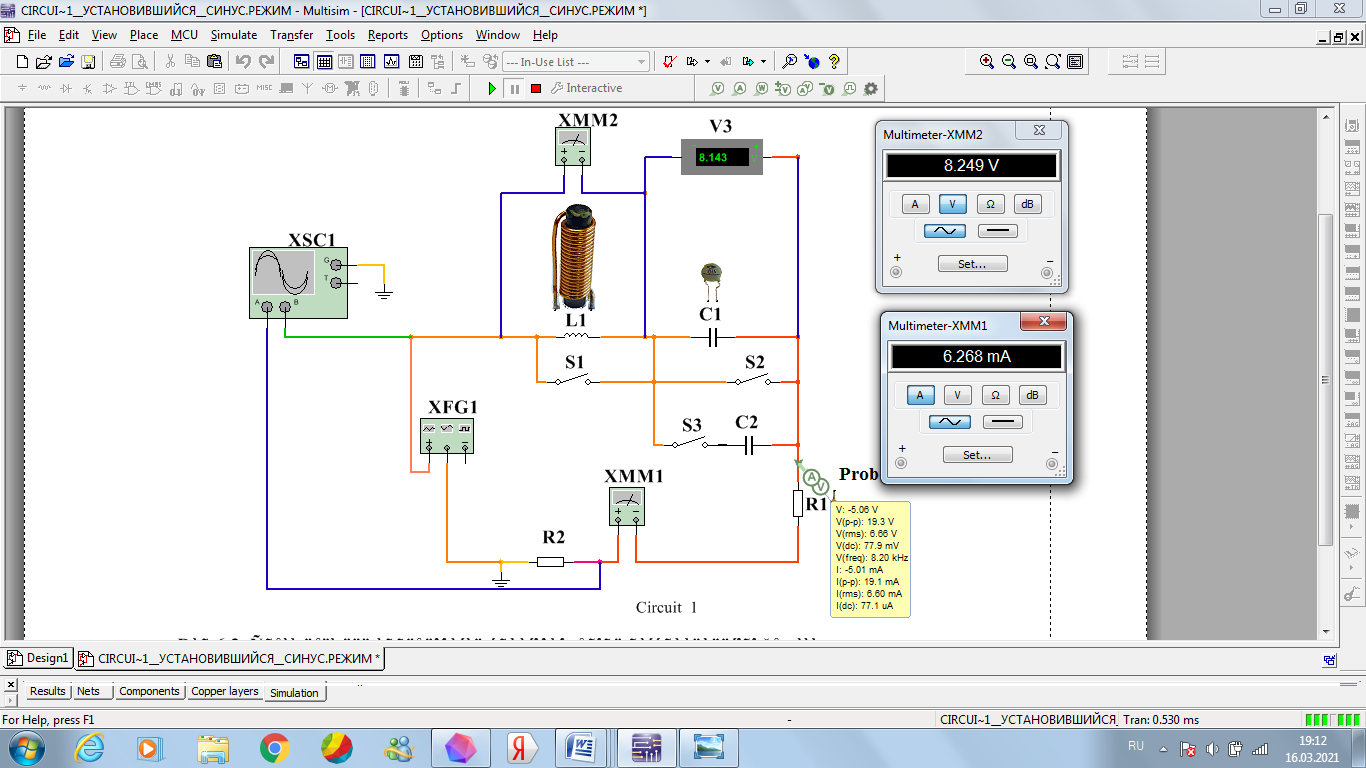
Рисунок 18 – схема RLC – цепи при 8,24 кГц

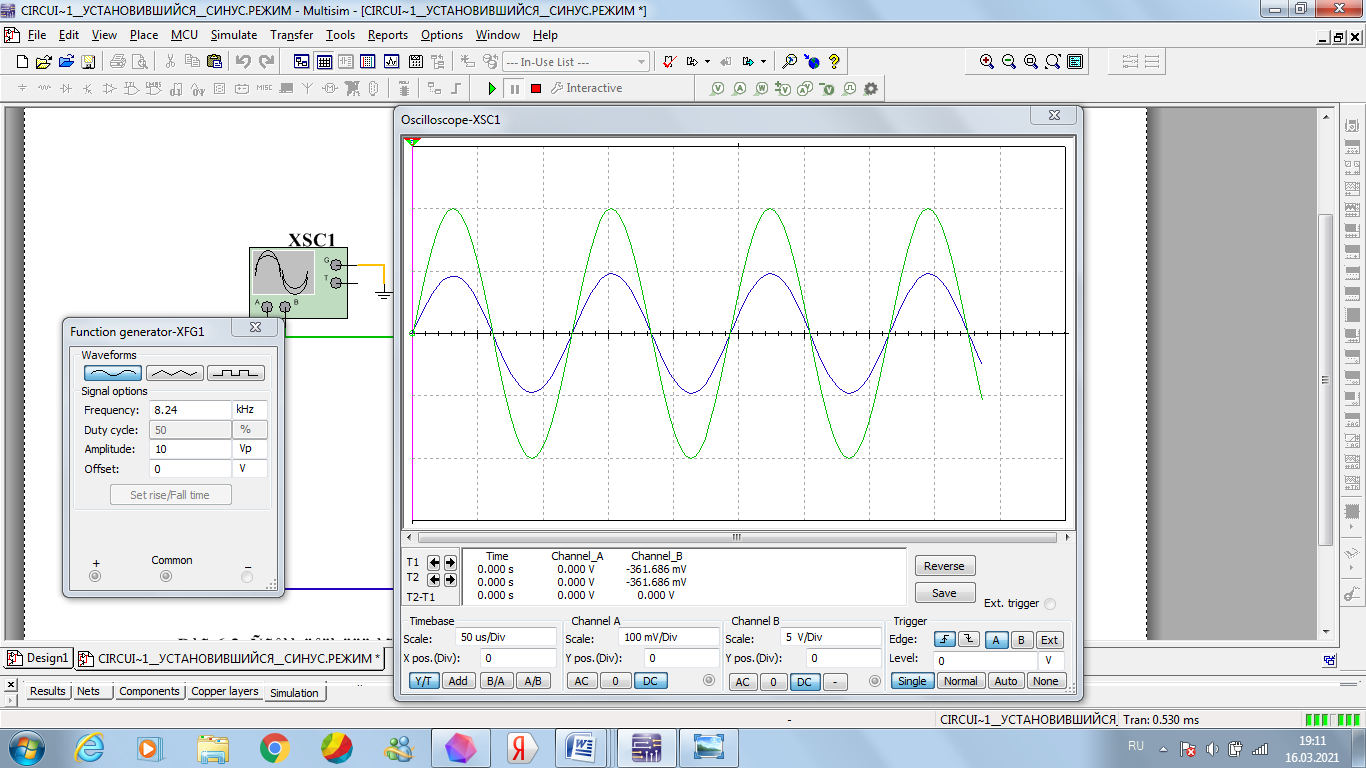
Рисунок 19 – осциллограмма входного напряжения и тока при 8,24 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

Рисунок 20 – векторная диаграмма тока и напряжений

Вычислим φос8,24:

Вычислим R, |Z_L|, L, |Z_C|, C:

R = U_R/I=

|Z_L| = U_L/I=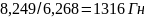

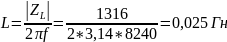
|Z_C| = U_C/I=

С =

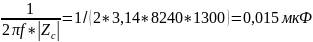
Занесем полученные значения в таблицу 1.

При 16,48 кГц:

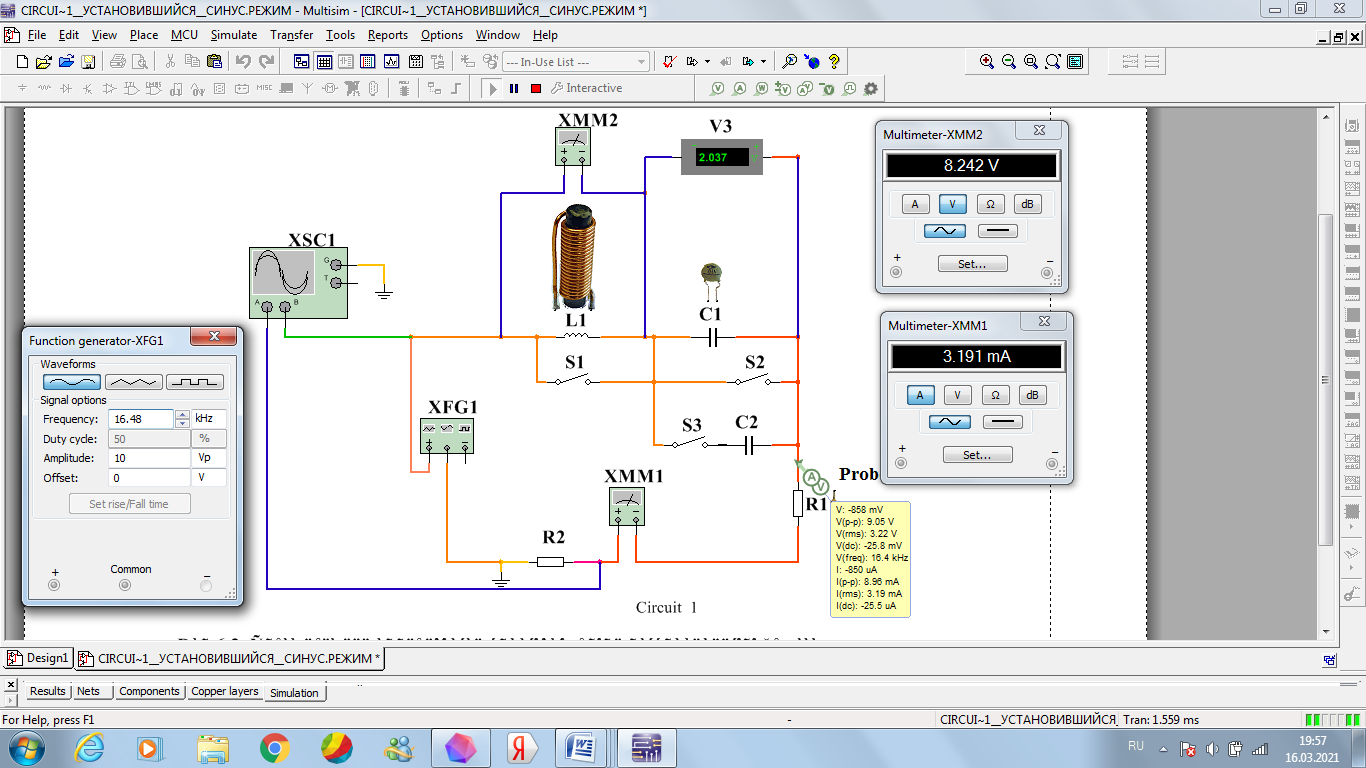
Рисунок 21 – схема RLC – цепи при 16,48 кГц

Рисунок 22 – осциллограмма входного напряжения и тока при 16,48 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

Рисунок 23 – векторная диаграмма тока и напряжений

Вычислим φос16,48:

Вычислим R, |Z_L|, L, |Z_C|, C:

R = U_R/I=

|Z_L| = U_L/I=

|Z_C| = U_C/I=

С =

Занесем полученные значения в таблицу 1.

При 4,12 кГц:

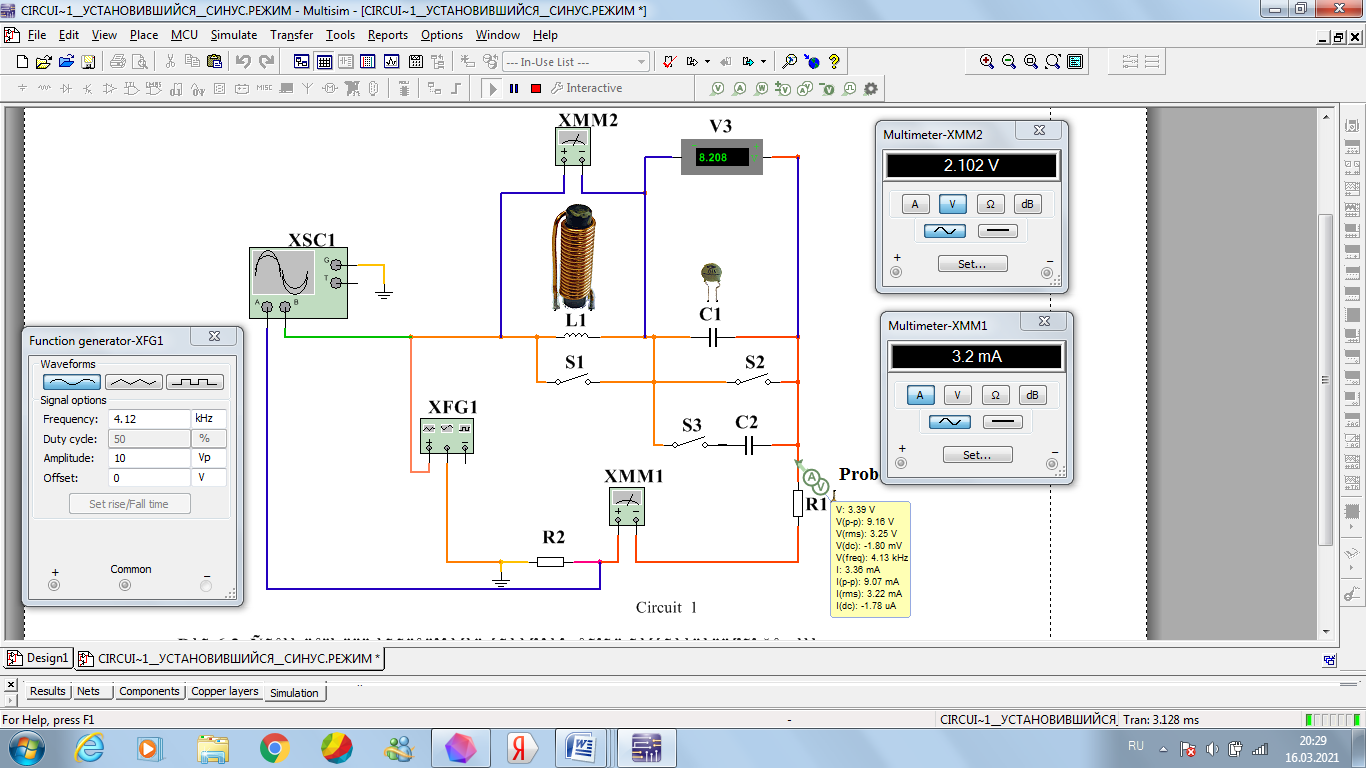
Рисунок 24 – схема RLC – цепи при 4,12 кГц

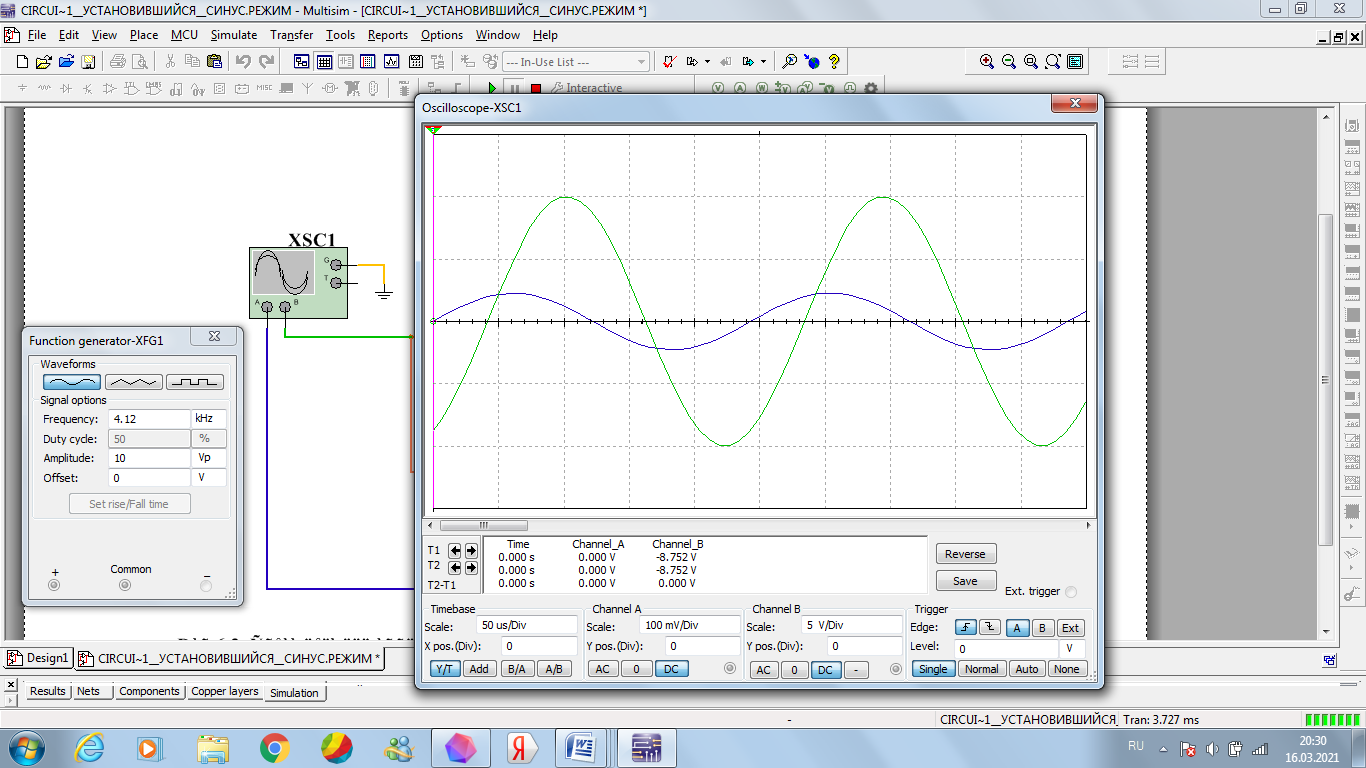
Рисунок 25 – осциллограмма входного напряжения и тока при 4,12 кГц

Зеленая – кривая напряжения, синяя – кривая тока.

Рисунок 26 – векторная диаграмма тока и напряжений

Вычислим φос4,12:

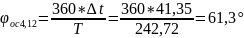
Вычислим R, |Z_L|, L, |Z_C|, C:

R = U_R/I=

|Z_L| = U_L/I=

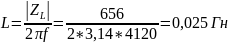
|Z_C| = U_C/I=

С =

Занесем полученные значения в таблицу 1.

Вывод: в ходе выполнения лабораторной работы были изучены синусоидальные режимы в простых RL, RC и RLC цепях; были определены индуктивность, емкость, сопротивление, комплексное сопротивление индуктивности и комплексное сопротивление емкости различных цепей при различных частотах; для каждой цепи были построены осциллограммы входного напряжения и тока, построены векторные диаграммы тока и напряжения.

Ответы на вопросы

1. Почему ?

Потому что ток в резисторе опережает напряжение на конденсаторе на 90°.

2. Почему при увеличении частоты величины I и U_R увеличились, а U_C и уменьшились? Изменились ли R и C?

Потому что обратно пропорционально частоте, поэтому при увелечении частоты уменьшается , что ведёт к уменьшению 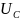и увелечению , ток увеличивается и уменьшается угол опережения напряжения. и – константы.

3. Почему ?

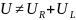Потому что ток в резисторе отстает от напряжения на катушке на 90°.

4. Почему ?

Из – за того, что ток в резисторе отстает от напряжения на катушке на 90°, напряжение на конденсаторе отстает от тока в резисторе на 90°.

5. Как изменятся величины 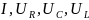и при увеличении частоты?

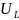При увеличении частоты значения , , уменьшаться, а и увеличатся. Так как прямо пропорционально частоте, при увеличении частоты увеличится , что ведёт к увеличению и уменьшению , ток уменьшится, и увеличится угол отставания от напряжения. Так как обратно пропорционально частоте, при увеличении частоты уменьшится.