Medvedev_9587_TOE_LR_3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №3

по дисциплине «Теоретические основы электротехники»

Тема: Исследование свободных процессов в электрических цепях

Студент гр. 9587		Медведев Г.Н.
Преподаватель		Яшкардин Р.В.

Санкт-Петербург

2021

Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Основные теоретические положения

В работе предлагается исследовать свободные процессы в цепях, схемы которых представлены на рисунке 1 (а – цепь первого порядка, б – цепь второго порядка, в - цепь третьего порядка). Цепи возбуждаются короткими импульсами тока i₀(t), заряжающими конденсатор C. В паузах между импульсами конденсатор разряжается; цепь находится в свободном режиме, так как в это время источник возбуждения отключен (i₀=0). Напряжения на элементах цепи осциллографируются.

Рисунок 1 – схемы цепей различных порядков

Поведение линейных цепей описывается линейными дифференциальными уравнениями; при этом вид свободного процесса определяется корнями p_k характеристического уравнения (собственными частотами цепи).

При возбуждении цепи источником тока собственные частоты можно рассчитать, как нули входной проводимости цепи Y(p), т.е. как корни уравнения Y(p)=0.

Для цепи первого порядка, , откуда

.

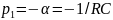Для цепи второго порядк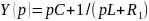а, , откуда

.

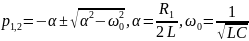Для цепи третьего порядка,

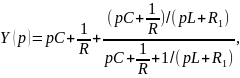
Откуда

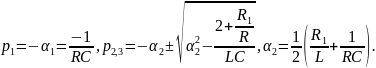
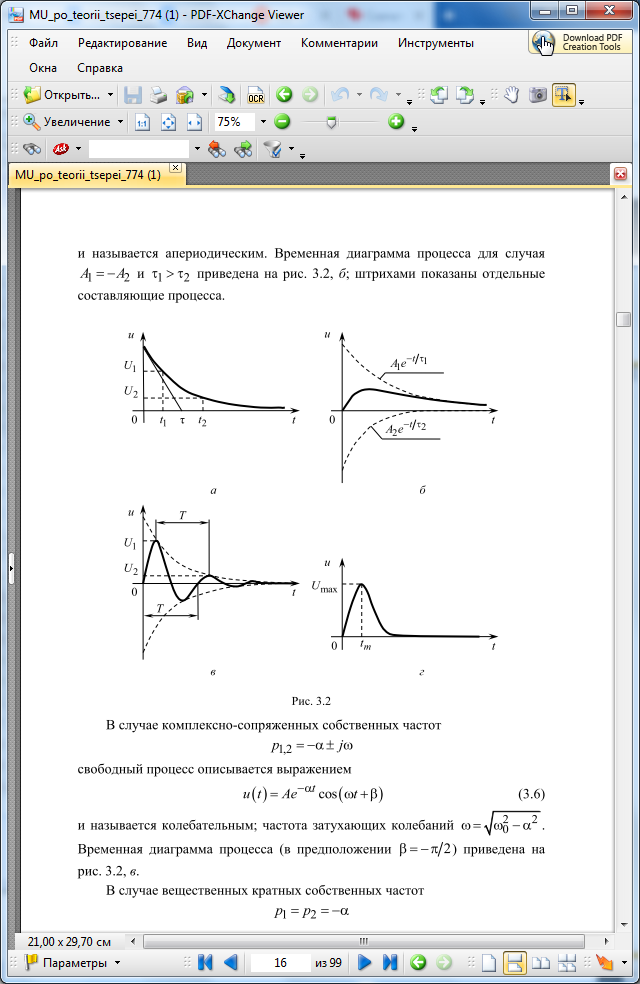
Рисунок 2 – временные диаграммы свободных процессов

У цепи первого порядка одна собственная частота 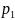- вещественная и отрицательная; свободный процесс описывается затухающей экспонентой (рисунок 2, а):

.

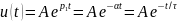У цепи второго порядка две собственные частоты 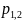могут быть вещественными (простыми или кратными) или комплексно-сопряженными.

В случае вещественных простых собственных частот

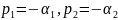11,

свободный процесс описывается суммой двух экспонент:

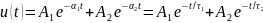
и называется апериодическим (рисунок 2, б).

В случае комплексно-сопряженных собственных частот

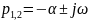
свободный процесс описывается выражением

и называется колебательным (рисунок 2, в).

В случае вещественных кратных собственных частот

свободный процесс описывается выражением

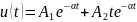
и называется критическим или предельным апериодическим (рисунок 2, г).

Дальнейшее увеличение порядка цепи к качественно новым явлениям не приводит. Собственные частоты могут быть либо все три вещественные, либо одна – вещественная и две – комплексно-сопряженные, например 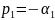и .

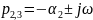Обработка экспериментальных результатов

1. Исследование свободного процесса в цепи первого порядка

Соберем цепь первого порядка:

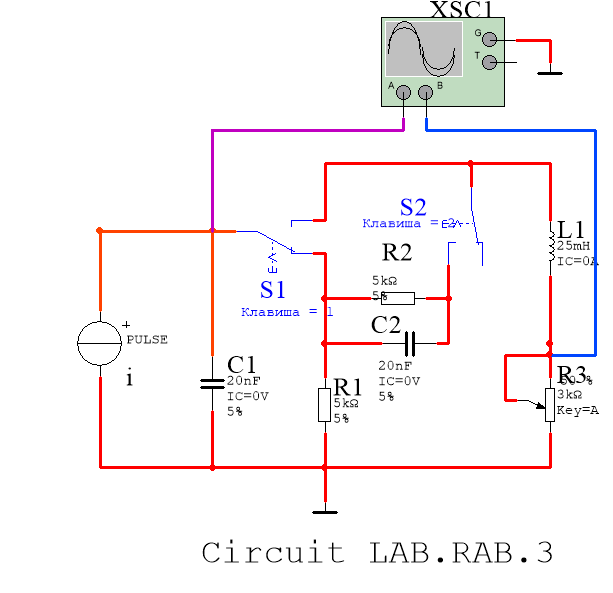
Рисунок 3 – схема цепи первого порядка

Снимем ее осциллограмму:

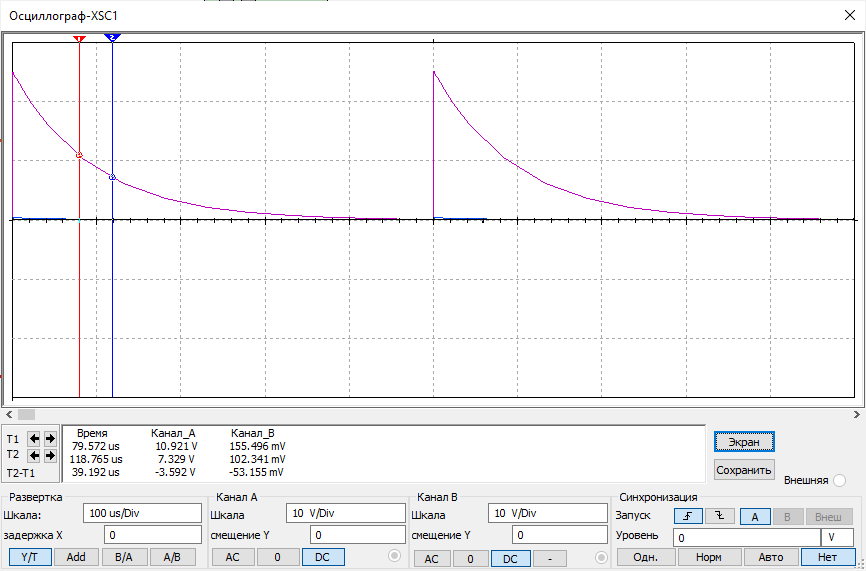
Рисунок 4 – осциллограмма цепи первого порядка

Найдем постоянную времени τ методом подкасательной:

U₁ = 10.921 B

U₂ = 7.329 B

∆t = 39.192 мкс

Найдем экспериментальное значение τ:

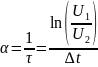
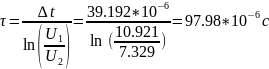
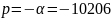
Найдем теоретическое значение τ:

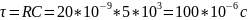
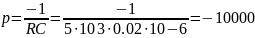
Экспериментальное и теоретическое значения близки (теоретическое больше экспериментального на 2.02 мкс).

Построим диаграмму расположение собственной частоты на комплексной плоскости:

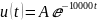
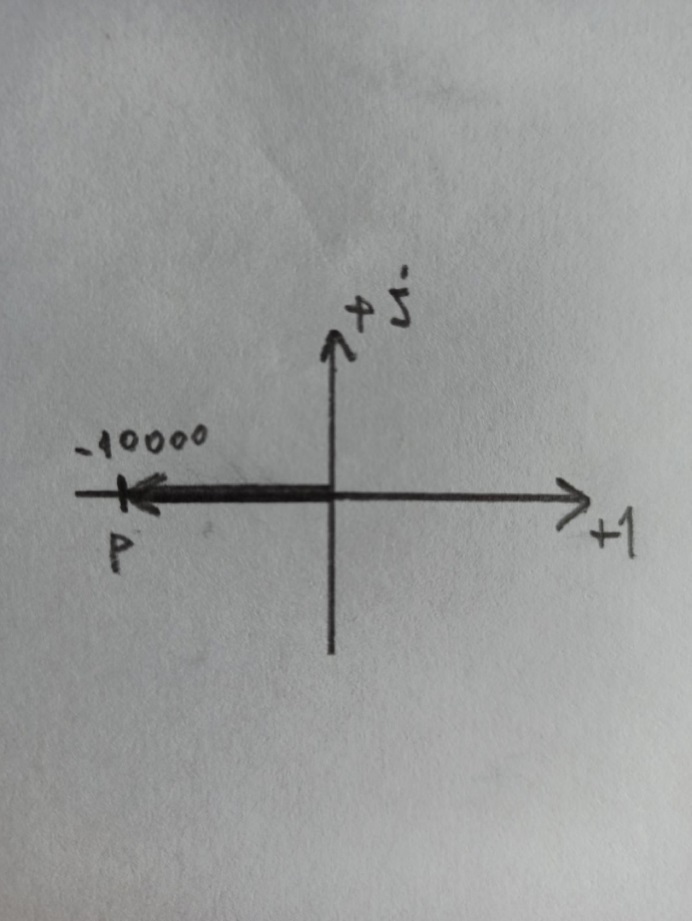
Рисунок 5 - расположение собственной частоты на комплексной плоскости

2. Исследование свободных процессов в цепи второго порядка

Соберем цепь второго порядка:

Рисунок 6 – схема цепи второго порядка

Меняя сопротивления потенциометра R_3, рассмотрим апериодический, колебательный и критический режимы.

1. Апериодический режим (R₃ = 3 кОм, 100%)

Снимем осциллограмму цепи при апериодическом режиме:

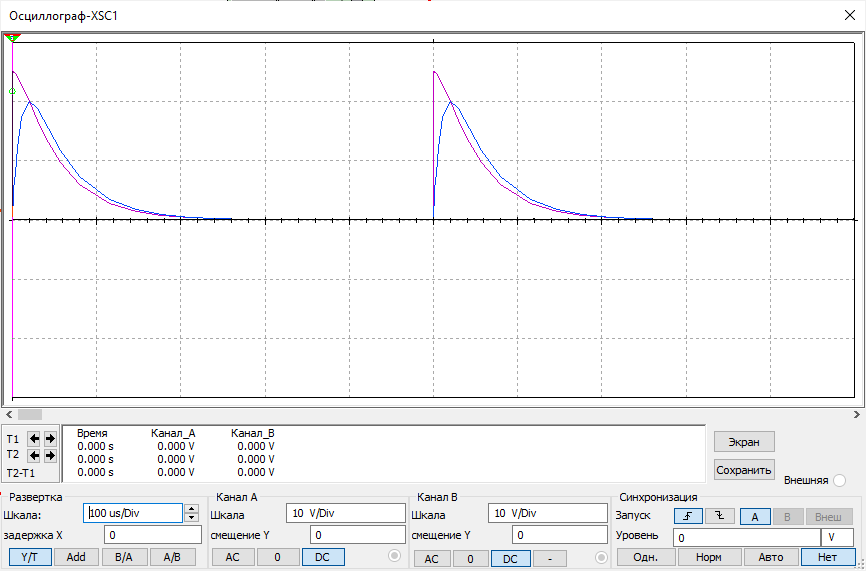
Рисунок 7 – осциллограмма цепи второго порядка (апериодический режим)

Рассчитаем теоретические параметры:

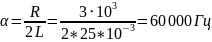
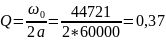< 0,5 – апериодический режим

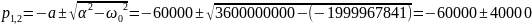
Построим диаграмму расположение собственных частот на комплексной плоскости:

Рисунок 8 - расположение собственных частот на комплексной плоскости

2. Колебательный режим (R₃ = 0,5 кОм, 17%)

Снимем осциллограмму цепи при колебательном режиме:

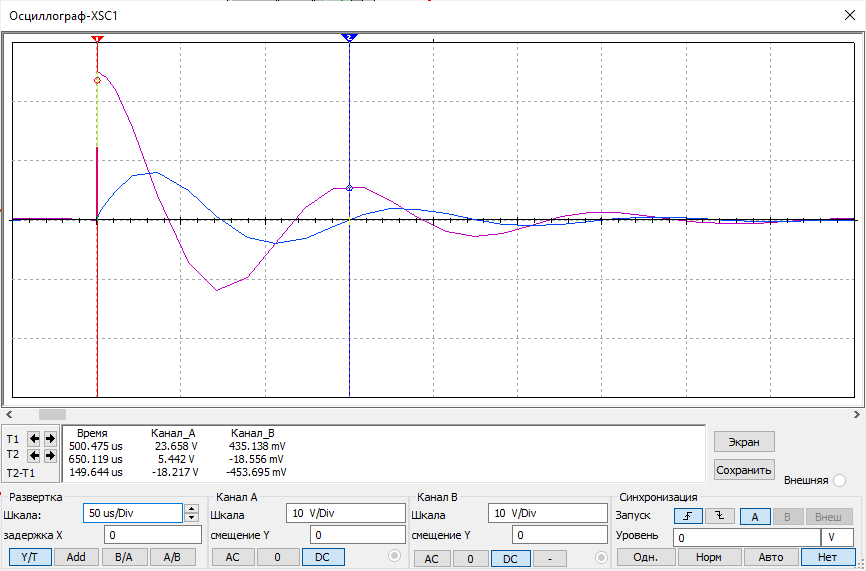
Рисунок 9 – осциллограмма цепи второго порядка (колебательный режим)

Рассчитаем теоретические параметры:

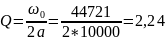> 0,5 – колебательный режим

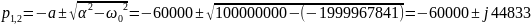
Построим диаграмму расположение собственных частот на комплексной плоскости:

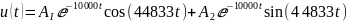
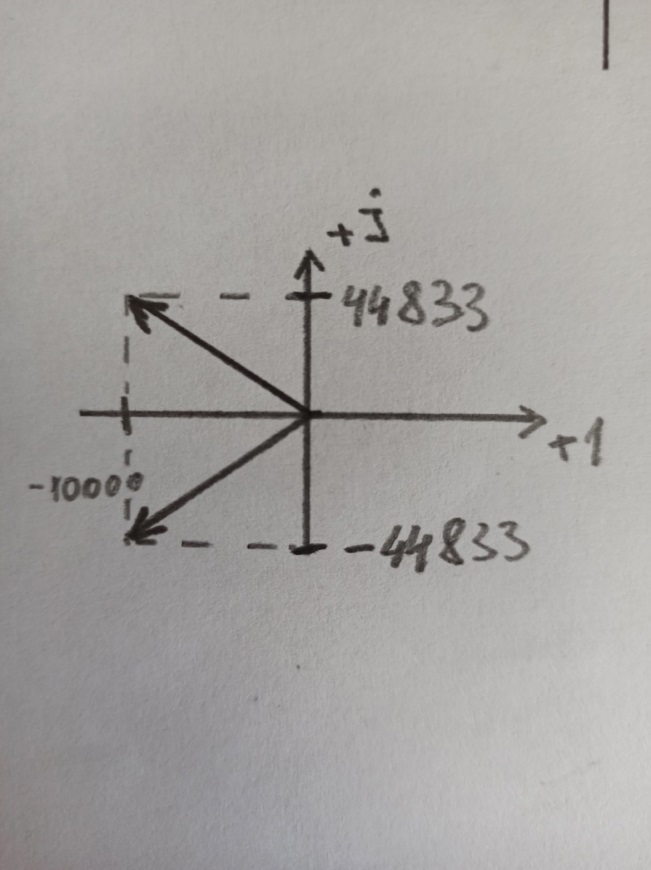
Рисунок 10 - расположение собственных частот на комплексной плоскости

Рассчитаем экспериментальные параметры:

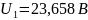
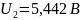
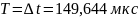
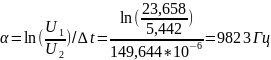
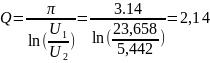> 0,5 – колебательный режим

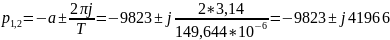
Экспериментальные и теоретические значения близки.

3. Колебательный режим при высокой добротности (R₃ = 30 Ом, 1%)

Снимем осциллограмму цепи при колебательном режиме при высокой добротности:

Рисунок 11 – осциллограмма цепи второго порядка (колебательный режим при высокой добротности)

Рассчитаем теоретические параметры:

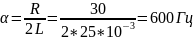
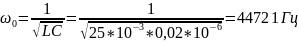
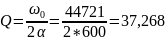> 0,5 – колебательный режим

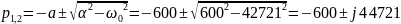
Построим диаграмму расположение собственных частот на комплексной плоскости:

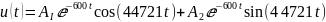
Рисунок 12 - расположение собственных частот на комплексной плоскости

4) Критический режим (R₃ 50 - 70%)

Снимем осциллограмму цепи при критическом режиме:

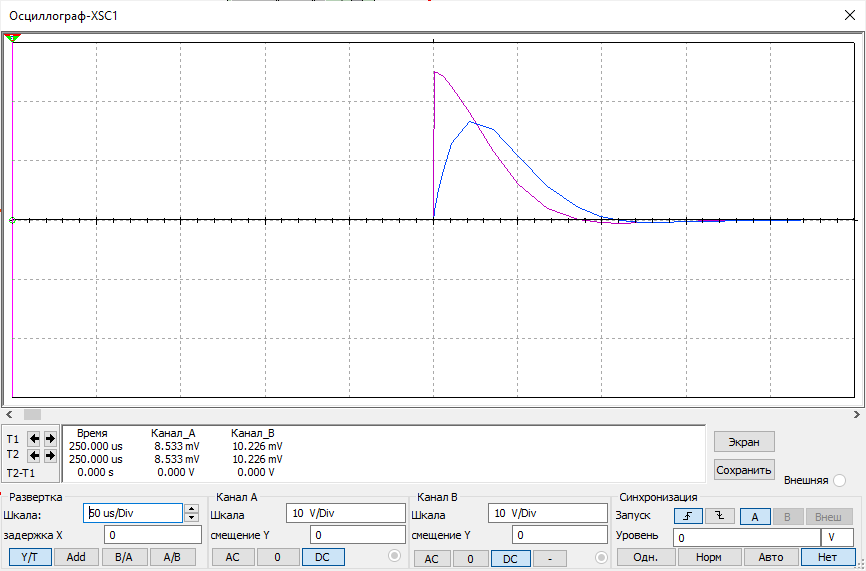
Рисунок 13 – осциллограмма цепи второго порядка (критический режим)

Рассчитаем теоретические параметры:

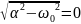
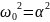
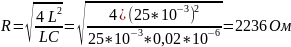
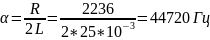
– критический режим

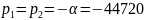
Построим диаграмму расположение собственных частот на комплексной плоскости:

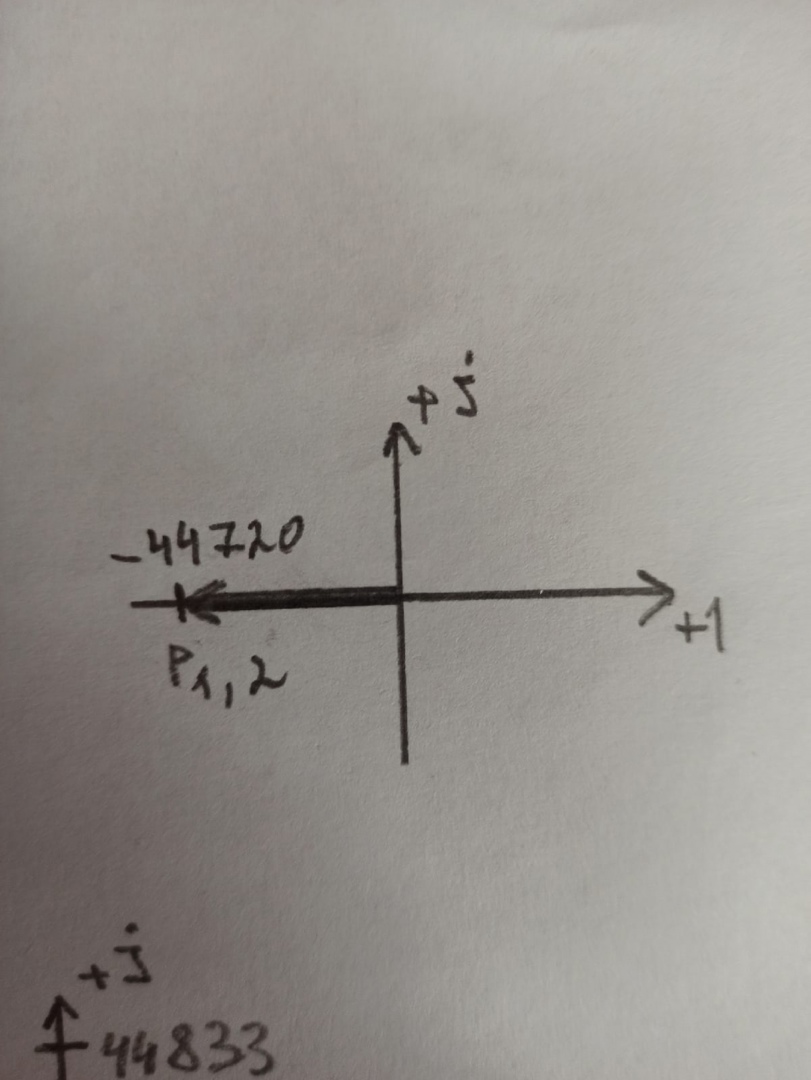
Рисунок 14 – расположение собственных частот на комплексной плоскости

3. Исследование свободных процессов в цепи третьего порядка

Соберем цепь третьего порядка:

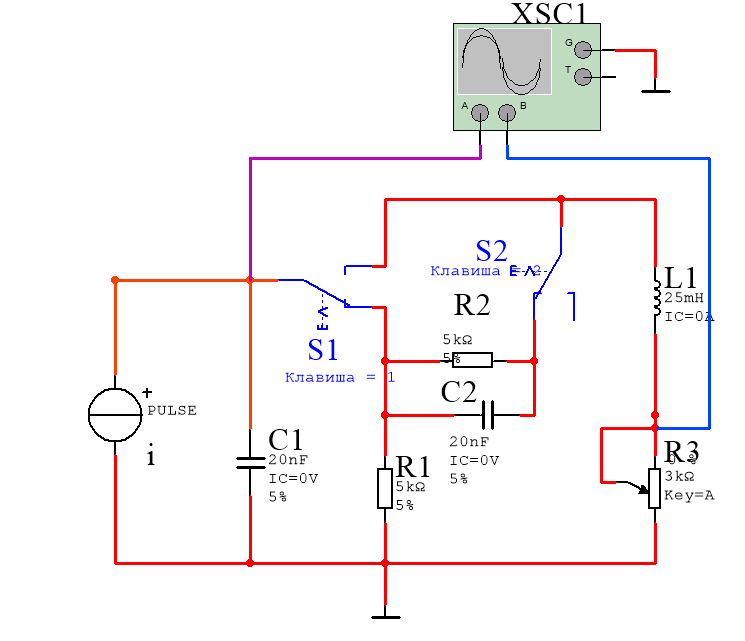
Рисунок 15 – схема цепи третьего порядка

Снимем ее осциллограмму:

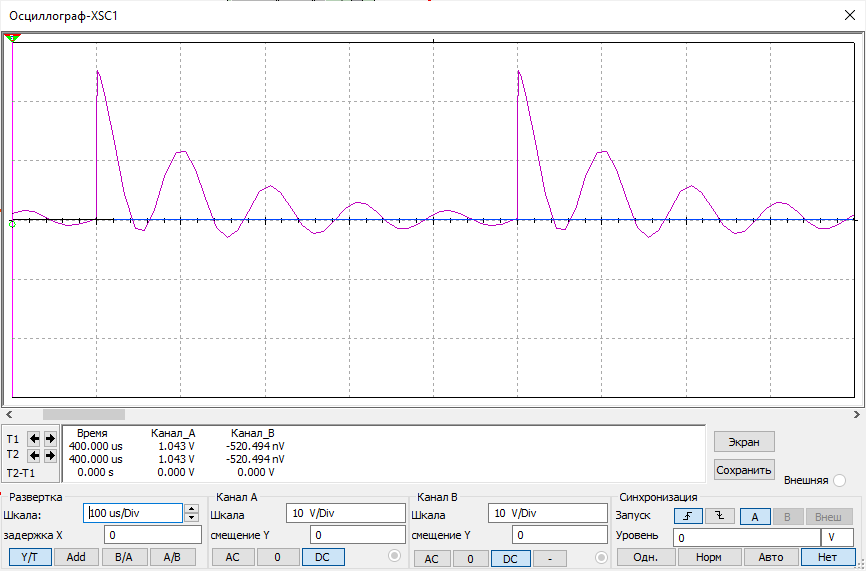
Рисунок 16 – осциллограмма цепи третьего порядка

Рассчитать теоретически частоты собственных колебаний:

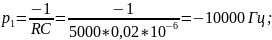
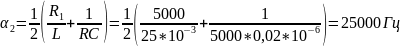
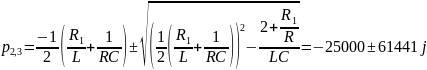
Построим диаграмму расположение собственных частот на комплексной плоскости:

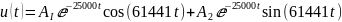
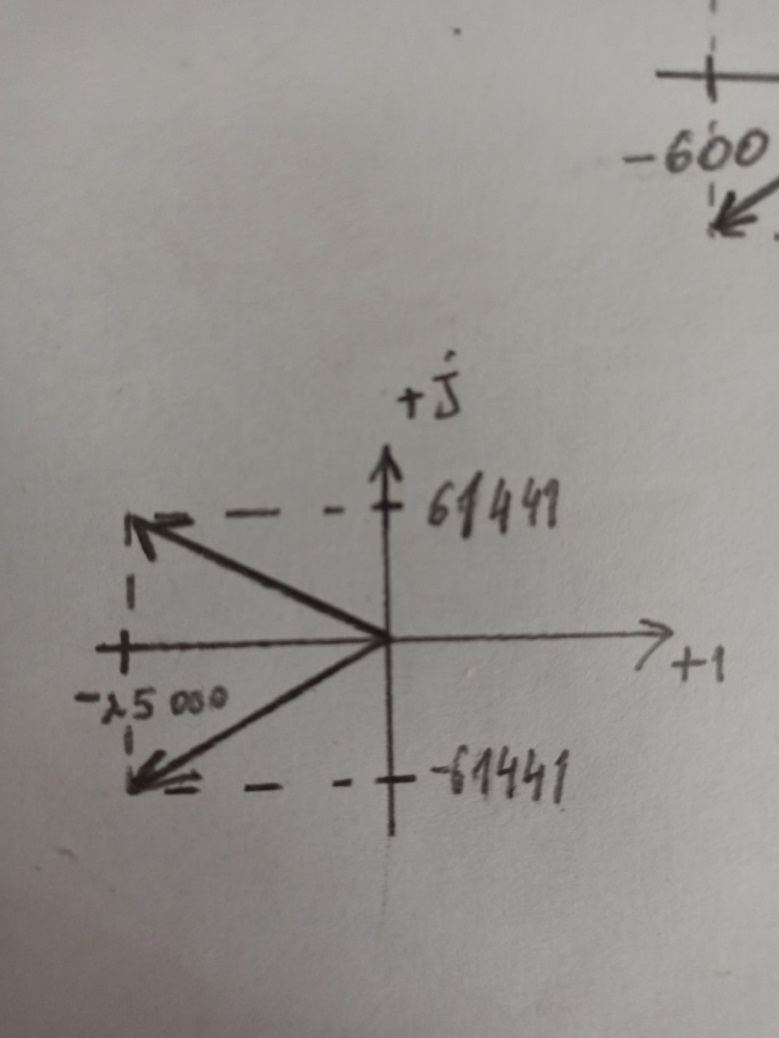
Рисунок 17 – расположение собственных частот на комплексной плоскости

Вывод: в ходе выполнения лабораторной работы была исследована связь между видом свободного процесса в электрической цепи и расположением собственных частот на комплексной плоскости; был применен метод подкасательной для поиска данных частот цепи первого порядка; для цепей второго порядка были рассмотрены все режимы; были экспериментально определены собственные частоты и добротность RLC-контуров по осциллограммам.

Ответы на вопросы

1. Каким аналитическим выражением описывается переходным процесс в цепи первого порядка?

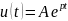
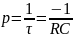
2. Как по осциллограмме определить собственную частоту цепи первого порядка? Соответствует ли она теоретическую расчету?

Собственную частоту 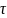можно определить с помощью метода подкасательной по осциллограммы.

Найденная таким образом собственная частота отличается от теоретической на 2%.

3. Какими аналитическими выражениями в общем виде описываются графики процессов во всех исследуемых цепях второго порядка? Как определить по осциллограмме, снятой при R₁=0,5 кОм, собственный частоты цепи второго порядка?

Для апериодического режима:

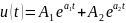
Для критического режима:

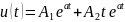
Для колебательного режима:

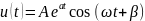
При R1 = 0,5 кОм в цепи устанавливается колебательный режим. Собственные частоты определяются по экспериментальной осциллограмме с помощью формул (методом подкасательной):

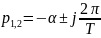
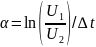
4. Каким аналитическим выражением описывается полученный график свободного процесса в цепи третьего порядка?

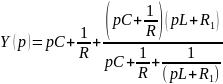
5. Каковы теоретические значения собственных частот цепи третьего порядка? Соответствует ли им осциллограмма и почему?

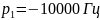
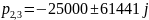
Исходя из знаний, полученных в ходе изучения цепи первого порядка (одна вещественная собственная частота) и цепи второго порядка в колебательном режиме (две комплексные собственные частоты), можно сделать вывод, что данная осциллограмма третьего порядка приближённо похожа на суперпозицию двух осциллограмм (цепей первого и второго (колебательный режим) порядков), а значит найденные собственные частоты соответствуют полученной осциллограмме.