лр4исправ
.docxОбработка результатов эксперимента
Таблица 1
N |
a, мм |
b, мм |
X, мкм |
|||||
1 |
210 |
108 |
413 |
454 |
412 |
428 |
450 |
435 |
2 |
185 |
130 |
463 |
488 |
503 |
483 |
488 |
504 |
3 |
145 |
170 |
613 |
644 |
620 |
616 |
650 |
625 |
4 |
125 |
190 |
613 |
681 |
737 |
706 |
700 |
704 |
5 |
115 |
200 |
788 |
837 |
708 |
725 |
754 |
761 |
6 |
85 |
230 |
1125 |
962 |
1050 |
1009 |
1047 |
1066 |
7 |
85 |
250 |
1200 |
1106 |
1070 |
1112 |
1085 |
1081 |
8 |
85 |
130 |
700 |
706 |
733 |
729 |
756 |
746 |
9 |
75 |
100 |
700 |
737 |
825 |
767 |
769 |
760 |
10 |
75 |
80 |
700 |
656 |
712 |
709 |
700 |
679 |
1. Вычислим значения преломляющего угла β бипризмы Френеля
Таблица 2
N |
β, рад |
|||||
1 |
0,00207 |
0,00188 |
0,00208 |
0,00200 |
0,00190 |
0,00197 |
2 |
0,00208 |
0,00197 |
0,00191 |
0,00199 |
0,00197 |
0,00191 |
3 |
0,00200 |
0,00191 |
0,00198 |
0,00199 |
0,00189 |
0,00196 |
4 |
0,00232 |
0,00209 |
0,00193 |
0,00202 |
0,00203 |
0,00202 |
5 |
0,00196 |
0,00185 |
0,00219 |
0,00213 |
0,00205 |
0,00203 |
6 |
0,00186 |
0,00218 |
0,00199 |
0,00208 |
0,00200 |
0,00196 |
7 |
0,00186 |
0,00201 |
0,00208 |
0,00200 |
0,00205 |
0,00206 |
8 |
0,00204 |
0,00202 |
0,00195 |
0,00196 |
0,00189 |
0,00192 |
9 |
0,00188 |
0,00179 |
0,00160 |
0,00172 |
0,00171 |
0,00173 |
10 |
0,00167 |
0,00178 |
0,00164 |
0,00165 |
0,00167 |
0,00172 |
Пример расчета значения β для X = 413 мкм:
β = λ*(a + b)/(2*X*a*(N-1)), при λ = 565*10-9 м, N = 1,5 (для стекла)
β (X = 413 мкм) = 0,565*10-9*(210 + 108)*10-3/(2*413*10-6*210*10-3*(1,5 - 1)) = 0,00207
2. Вычислим среднее значение, СКО и случайную погрешность преломляющего угла β бипризмы Френеля
=
=
(0,00207+0,00188+…+0,00167+0,00172)/60
= 0,00194
3. Вычислим погрешность косвенных измерений полную погрешность преломляющего угла β бипризмы Френеля
Пример
расчета значения
для X
= 413 мкм:
=
0,000004
Таблица 3
|
|||||
0,000004 |
0,000004 |
0,000004 |
0,000004 |
0,000004 |
0,000004 |
0,000005 |
0,000004 |
0,000004 |
0,000004 |
0,000004 |
0,000004 |
0,000005 |
0,000005 |
0,000005 |
0,000005 |
0,000005 |
0,000005 |
0,000007 |
0,000006 |
0,000006 |
0,000006 |
0,000006 |
0,000006 |
0,000006 |
0,000006 |
0,000007 |
0,000007 |
0,000007 |
0,000007 |
0,000009 |
0,000010 |
0,000009 |
0,000010 |
0,000009 |
0,000009 |
0,000009 |
0,000009 |
0,000010 |
0,000009 |
0,000010 |
0,000010 |
0,000009 |
0,000009 |
0,000008 |
0,000008 |
0,000008 |
0,000008 |
0,000009 |
0,000009 |
0,000008 |
0,000008 |
0,000008 |
0,000008 |
0,000008 |
0,000009 |
0,000008 |
0,000008 |
0,000008 |
0,000008 |
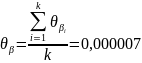
Вывод: в ходе выполнения лабораторной работы было исследовано явление интерференции с помощью бипризмы Френеля; была получена четкая интерференционная картина, по графикам которой было найдено расстояние между максимумами, в результате было рассчитано значение преломляющего угла бипризмы β и вычислены его погрешности.