ЦИУ_Лаб4 исправ

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИИСТ

отчет

по лабораторной работе №4

по дисциплине «Цифровые измерительные устройства»

ТЕМА: Определение основной погрешности АЦП

Студенты гр. 9587		Медведев Г.Н. Постникова Е.И. Сомов В.А.
Преподаватель		Поливанов В.В.

Санкт-Петербург

2022

Цель работы

1. Изучить способы экспериментального определения метрологических характеристик АЦП.

2. Экспериментально определить метрологические характеристики АЦП.

Задание на работу

Экспериментально определить метрологические характеристики АЦП:

1. Среднеквадратическое отклонение случайной погрешности

2. Предельные значения погрешности

3. Аддитивную и мультипликативные составляющие систематической погрешности

4. Инструментальную погрешность

Теоретические сведения

Статическая характеристика преобразования. Эта характеристика ЦИУ устанавливает связь между преобразуемой (входной) величиной X и результатом преобразования, за который принимается значение Nq, где N - значение выходного кода, q - квант. Для идеального ЦИУ характеристика преобразования имеет вид показанный на рис. 1 и получена при квантовании путем отождествления с ближайшем уровнем квантования. Изменения значений кода идеального ЦИУ со значений N-1 на N происходят при фиксированных значениях входной величины равных (N-0,5)q, где N - целое число.

Статическая характеристика определяется значением единицы младшего разряда кода, равной кванту q . Значение q может быть найдено при заданном диапазоне измерения (Xмin, Xmax), числе разрядов выходного кода n по формуле для АЦП q = (Xmax - Xмin -) / 2n или q = (Xmax - Xмin -) / 10n для цифрового прибора.

Характеристика реального ЦИУ отличается от идеальной. Различие проявляется в том, что изменение значений выходного кода ЦИУ происходит при отличных от идеального случая значениях входной величины. Причина этого – наличие инструментальных погрешностей ЦИУ. Инструментальная погрешность определяется для некоторого значения выходного кода N (см. рис.1) по отличию реальной характеристики ЦИУ от идеальной

Xи(N)= (N-0.5)q – ХкN,

где ХкN – значение входной величины, при котором значение кода меняется со значения N - 1 на N.

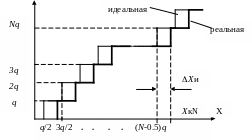
Рис. 1 Статическая характеристика преобразования ЦИУ

Статические погрешности ЦИУ. Абсолютное значение статической погрешности ЦИУ может быть определено по формуле

X = Xр - X = Nq - X,

где Xр= Nq – результат измерения, N - выходной код ЦИУ, q - квант, X – истинное значение измеряемой величины.

В соответствии с принятой классификацией погрешности делятся на отдельные составляющие. По причинам возникновения погрешности делятся на методические и инструментальные. К методическим погрешностям относят погрешности, обусловленные несовершенством принятого метода измерения (погрешность квантования по уровню), под инструментальными–погрешности обусловленные несовершенством технической реализации ЦИУ.

Погрешность квантования при произвольном входном сигнале рассматривается как случайная величина. В качестве характеристик погрешности квантования используются предельные значения, среднеквадратическое отклонение погрешности.

Для идеального ЦИУ квантование осуществляется путем отождествления с ближайшим или равным уровнем квантования, погрешность квантования имеет равномерную плотность распределения на интервале [-q/2;+q/2], среднеквадратическое отклонение погрешности равно q/(23). Предельные значения абсолютной погрешности квантования равно X = q/2, Приведенная погрешность квантования при заданном числе разрядов АЦП n равна  =  (100/2n+1) % , а для ЦИП при числе разрядов m десятичного ЦОУ  =  (100/2 10m) %.

В зависимости от характера изменения погрешности по диапазону измерения СИ погрешности делятся на аддитивные и мультипликативные. Аддитивные погрешности не зависят от значения измеряемой величины X, мультипликативные растут с увеличением X. Обычно для CИ погрешность задается в виде модели

X = a + bX,

где a и bX - аддитивная и мультипликативная составляющая погрешности соответственно.

По характеру изменения погрешности при повторных измерениях одного и того же значения погрешности делятся на систематические и случайные. Систематические остаются постоянными или меняются закономерным образом, значения случайных погрешностей можно предсказать с некоторой вероятностью. В общем случае погрешность является случайной величиной и ее можно представить в виде

X = Xсист + Xсл

где =M[X] – систематическая погрешность (математическое ожидание погрешности); – случайная составляющая погрешности.

Для оценки значений погрешности как случайной величины применяются характеристики: среднеквадратическое отклонение погрешности (СКО) (корень квадратный из дисперсии); доверительный интервал, задаваемый верхней и нижней границами и доверительная вероятность , связанные соотношением , где P{ }–вероятность выполнения неравенства в { }.

При =1 и симметричном относительно нулевого значения доверительном интервале в качестве характеристики погрешности используется граничные (предельные) значения погрешности равные  .

Обработка результатов эксперимента

1. Определим значение кванта по уровню для АЦП

q = (X_мin - X_max) / 2ⁿ

q = 10/2⁸ = 0,03906 В

2. Определим значения СКО случайной погрешности  и систематической погрешности ΔUсист

Пример расчета для первого измерения:

 = _Nq

 = 1,359 * 0,0391 = 0,05 В

ΔUсист = Ňq – Uо

ΔUсист = 21,714 * 0,0391 – 0,749 = 0,1 В

Таблица 1

№	Uо , В	N,	, В	Ň , В	ΔUсист, В	ΔUмин, В	ΔUмакс, В
1	0,749	1,359	0,0531	21,714	0,1	-0,0068	0,1885
2	1,357	1,326	0,0518	37,102	0,09	0,0102	0,1664
3	2,535	1,330	0,0520	66,910	0,08	0,0041	0,1603
4	3,614	1,375	0,0537	94,099	0,06	-0,0202	0,1360
5	4,733	1,370	0,0535	122,495	0,05	-0,0455	0,1498
6	5,856	1,345	0,0525	150,857	0,04	-0,0357	0,1206
7	6,977	1,317	0,0514	179,228	0,02	-0,0629	0,0933
8	8,183	1,355	0,0529	209,773	0,01	-0,0971	0,0983
9	9,572	1,340	0,0523	244,916	-0,005	-0,0798	0,0764

Построим графики зависимости СКО случайной погрешности  и систематической погрешности ΔUсист от значения измеряемого напряжения Uо

Рисунок 1 - график зависимости СКО случайной погрешности от значения измеряемого напряжения

Рисунок 2 - график зависимости систематической погрешности от значения измеряемого напряжения

Систематическая погрешность линейно уменьшается с ростом входного напряжения

По графику определим аддитивную и мультипликативную составляющие систематической погрешности

ΔU_сист = a + bU_{0, где a – аддитивная, bU0 – мультипликативная составляющие}

ΔU_сист = (0,11 – 0,016U_{0) В}

a = 0,11 В

b U₀ = -0,016 U_{0 В}

3. Построим график зависимости инструментальной погрешности АЦП ΔUи от измеряемого напряжения Uо_N

Таблица 2

№	UоN, В	Ni	Ui, В	ΔUи, В
1	1,893	52	2,031	0,138
2	2,628	71	2,773	0,145
3	3,75	100	3,906	0,156
4	4,871	129	5,039	0,168
5	5,993	158	6,172	0,179
6	7,115	187	7,305	0,190
7	8,352	219	8,555	0,203
8	9,590	251	9,805	0,215

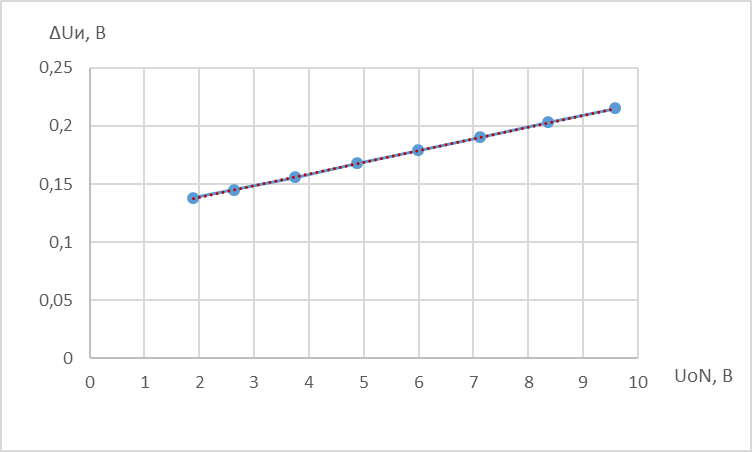
Рисунок 3 - график зависимости инструментальной погрешности АЦП от измеряемого напряжения

Инструментальная погрешность линейно увеличивается с ростом входного напряжения

По графику определим аддитивную и мультипликативную составляющие систематической погрешности

ΔU_и = a + bU_{0N, где a – аддитивная, bU0N – мультипликативная составляющие}

ΔU_и = (0,12 + 0,01U_{0N) В}

a = 0,12 В

b U_0N = 0,01 U_{0N В}

_{Вывод: в ходе выполнения лабораторной работы были экспериментального определены метрологические характеристики АЦП:}

1. q = 0,03906 В;

2. _max = 0,05 В_;

3. ΔUсист = (0,11 – 0,016U₀) В;

4. ΔU_и = (0,12 + 0,01U_{0N) В}.