ЦИУ_Лаб1(исправ округления и вывод)

Обработка результатов эксперимента

1. Вычислим значение шага квантования по уровню q

_q = U_m /10³, U_{m – предел измерения}

q = 10/1000 = 0,01В

2. Вычислим значения систематической погрешности U_{сист и занесем результаты в таблицу 1.}

_{Пример расчета} U_{сист для первого измерения:}

_ΔU_{сист =} U₀ - 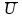= 1,121 – 1,166 = 0,05 В

_{Таблица 1}

Номер измерения	U0, В	, В	, В	ΔUсист, В	ΔUmin, В	ΔUmax, В
1	1,121	0,0165	1,166	0,05	0,019	0,069
2	2,353	0,0164	2,363	0,01	0,009	0,069
3	3,424	0,0168	3,464	0,04	0,006	0,066
4	4,380	0,0169	4,380	0,00	0,007	0,067
5	5,222	0,0169	5,257	0,04	0,008	0,068
6	6,131	0,0165	6,164	0,03	0,009	0,059
7	7,031	0,0168	7,063	0,03	-0,001	0,059
8	8,331	0,0171	8,358	0,027	-0,001	0,059
9	9,748	0,0170	9,772	0,024	-0,008	0,052

3. Построим график зависимости СКО случайной погрешности от измеряемого напряжения  = F(U0)

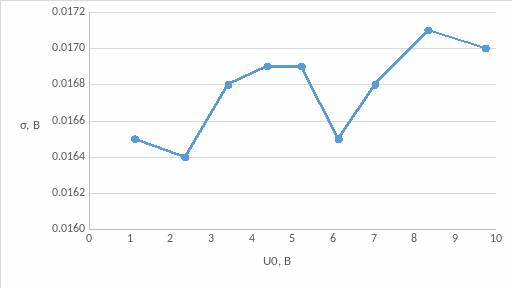
Рисунок 1 - график зависимости СКО случайной погрешности от измеряемого напряжения

4. Построим график зависимости систематической погрешности от измеряемого напряжения ΔUсист = F(U0) и оценим аддитивную и мультипликативную составляющие погрешности

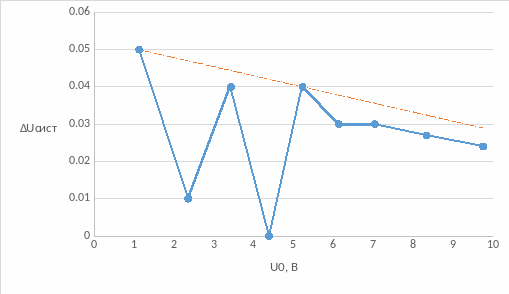
Рисунок 2 - график зависимости систематической погрешности от измеряемого напряжения

_Uсист = a + bU_{0, где a – аддитивная, bU0 – мультипликативная составляющие}

_Uсист = (0,05 – 0,0024U_{0) В}

_{a = 0,05 В; b U0 = - 0,0024 U0 В}

4. Построим графики начального участка статической характеристики вольтметра U_x = F(U₀) и зависимости погрешности квантования U_к = F(U₀) – U₀ от измеряемого напряжения U₀

Таблица 2

Номер измерения	U0, В	Ux, В	ΔUк, В
1	0,005	0,01	0,005
2	0,015	0,02	0,005
3	0,025	0,03	0,005
4	0,035	0,04	0,005
5	0,045	0,05	0,005

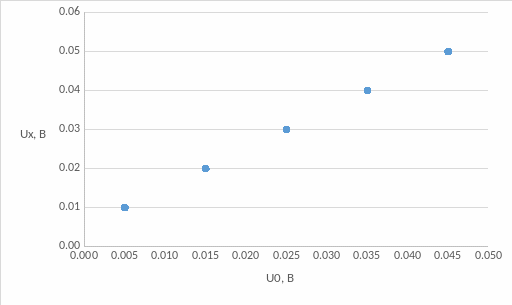
Рисунок 3 - график начального участка статической характеристики вольтметра

Рисунок 4 – график зависимости погрешности квантования от измеряемого напряжения

4. Построим график зависимости инструментальной погрешности от измеряемого напряжения ΔU_и = F(U₀) и оценим аддитивную и мультипликативную составляющие погрешности

Вычислим значения инструментальной погрешности и занесем результаты в таблицу 3.

Пример расчета ΔU_и для первого измерения:

ΔU_и = (U_x – 0,5q) – U_{0 = (1,39 – 0,5*0,01) – 1,346 = 0,04 В}

Таблица 3

Номер измерения	U0, В	Ux, В	ΔUи, В
1	1,346	1,39	0,04
2	2,433	2,48	0,04
3	3,719	3,77	0,05
4	4,417	4,47	0,05
5	5,514	5,57	0,05
6	6,212	6,27	0,05
7	7,648	7,71	0,06
8	8,765	8,83	0,06
9	9,483	9,55	0,06

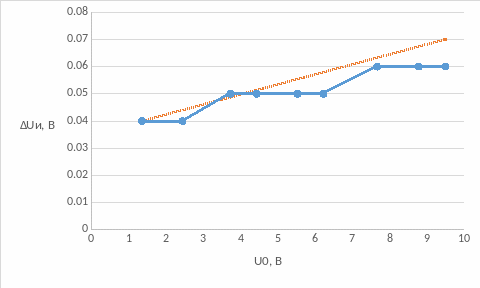
Рисунок 5 - график зависимости инструментальной погрешности от измеряемого напряжения

_Uи = a + bU_{0, где a – аддитивная, bU0 – мультипликативная составляющие}

_Uи = (0,03 + 0,003U_{0) В}

_{a = 0,03 В; b U0 = 0,003 U0 В}

_{Вывод: в ходе выполнения лабораторной работы были экспериментально определены метрологические характеристики цифрового вольтметра:}

1. _{q = 0,01 B;}

2. _max = 0,017_;

3. _ΔUсист = (0,05 – 0,0024U_{0) В;}

4. _ΔU_и = (0,03 + 0,003U_{0) В.}