LR5_VSMIIT

МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра ИИСТ

ОТЧЕТ по лабораторной работе №5

по дисциплине «Вероятностно-статистические методы в информационно-измерительной технике»

Тема: Статистическое моделирование. Метод Монте-Карло.

Санкт-Петербург

2022 г.

Цель работы: по заданной преподавателем схеме найти доверительный интервал для определяемого параметра Z, при заданной функции Z = F(X, Y) с помощью метода статистических испытаний. Закон распределения каждой из СВ X, Y считать: а – равномерным, б и в – нормальным. Закон распределения определяемого параметра Z принять нормальным.

Задание:

Ход работы:

1.Закон распределения случайных величин X и Y равномерный:

Код программы:

X= ax+vx*(bx-ax);

Y= ay+vy*(by-ay);

Z= (Y./X)+1;

mZ = mean(Z); sZ = std(Z); up = 2.6;

delta_Z = up*sZ; Z1 = mZ + delta_Z; Z2 = mZ - delta_Z;

figure (1) subplot (2,3,1)

histogram (vx,'FaceColor', 'r');

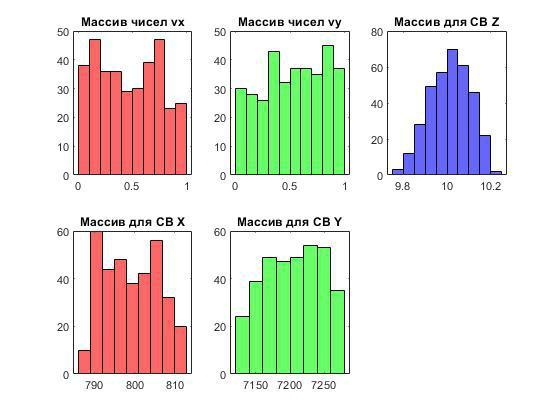
title('Массив чисел vx');

subplot (2,3,2)

histogram (vy,'FaceColor', 'g'); title({'Массив чисел vy'});

subplot (2,3,3)

histogram (Z,'FaceColor', 'b'); title('Массив для СВ Z');

subplot (2,3,4)

histogram (X,'FaceColor', 'r'); title('Массив для СВ X');

subplot (2,3,5)

histogram (Y,'FaceColor', 'g'); title('Массив для СВ Y');

Гистограммы СВ:

Доверительный интервал для параметра Z:

= ± _= 10,0149 ± 0,2399

2.Закон распределения случайных величин X и Y нормальный:

Код программы:

clc; clear all; close all; N = 350;

n = 5; MX = 800;

MY = 7200;

EX = 12;

EY = 72;

SX = EX/3; SY = EY/3;

mx = MX/n; sx = SX/sqrt(n); my = MY/n; sy = SY/sqrt(n);

ax = mx-sqrt(3)*sx; bx = mx+sqrt(3)*sx; ay = my-sqrt(3)*sy; by = my+sqrt(3)*sy; for i=1:N

x1 = rand(1,n);

x= ax+x1*(bx-ax); X(i) = sum(x);

y1 = rand(1,n);

y= ay+y1*(by-ay); Y(i) = sum(y);

Z(i) = (Y(i)./X(i))+1;

end

i = 1:N;

mZ = mean(Z(i)); sZ = std(Z(i)); up = 2.6; delta_Z = up*sZ;

Z1 = mZ + delta_Z;

Z2 = mZ - delta_Z;

figure (1) subplot (3,3,1)

histogram (x1,'FaceColor', 'r'); title('Массив чисел x1');

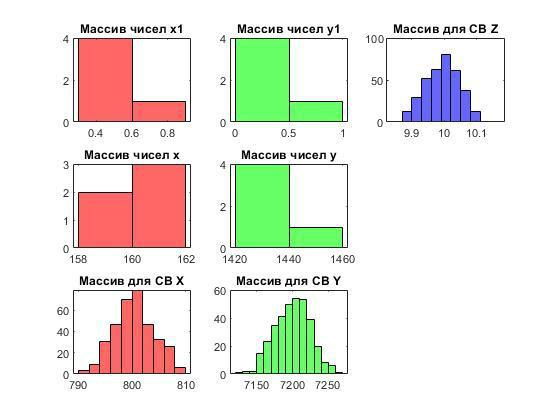
subplot (3,3,2)

histogram (y1,'FaceColor', 'g'); title({'Массив чисел y1'});

subplot (3,3,3)

histogram (Z,'FaceColor', 'b'); title('Массив для СВ Z');

subplot (3,3,4)

histogram (x,'FaceColor', 'r'); title('Массив чисел x');

subplot (3,3,5)

histogram (y,'FaceColor', 'g'); title({'Массив чисел y'});

subplot (3,3,7)

histogram (X,'FaceColor', 'r'); title('Массив для СВ X');

subplot (3,3,8)

histogram (Y,'FaceColor', 'g'); title('Массив для СВ Y');

Гистограммы СВ:

Доверительный интервал для параметра Z:

= ± _

= 9,9945 ± 0,1366

3.Проверим полученные результаты, используя готовый генератор стандартных нормально распределённых величин:

Код программы:

X = MX+vx*SX;

Y = MY+vy*SY;

Z = (Y./X)+1; i = 1:N;

mZ = mean(Z(i)); sZ = std(Z(i)); up = 2.6; delta_Z = up*sZ;

Z1 = mZ + delta_Z;

Z2 = mZ - delta_Z;

figure (1) subplot (2,3,1)

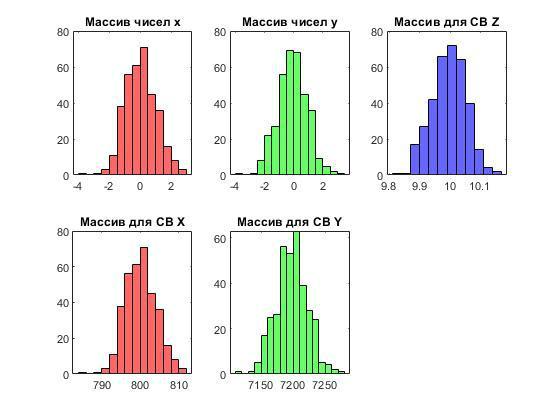
histogram (vx,'FaceColor', 'r'); title('Массив чисел x');

subplot (2,3,2)

histogram (vy,'FaceColor', 'g'); title({'Массив чисел y'});

subplot (2,3,3)

histogram (Z,'FaceColor', 'b'); title('Массив для СВ Z');

subplot (2,3,4)

histogram (X,'FaceColor', 'r'); title('Массив для СВ X');

subplot (2,3,5)

histogram (Y,'FaceColor', 'g'); title('Массив для СВ Y');

Гистограммы СВ:

Доверительный интервал для параметра Z:

= ± _

= 9,9960 ± 0,1431

Вывод: в ходе лабораторной работы была написана программа для определения доверительного интервала определяемого параметра Z, при заданной функции Z = F(X,Y) с помощью метода статистического моделирования, а также построены графики законов распределений СВ.