Вопрос 14.

Однородные СЛОДУ.

ОСЛОДУ

матрица непрерывна на функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы называется ЛЗ, если нетривиальный набор чисел (2) . Если тождество (2) выполняется только при , то система ЛНЗ

Свойства решений ОСЛОДУ

1. (Тривиальность) ОСЛОДУ (1) всегда обладает решением 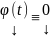Док-во: очевидно

2. (Линейность) Если 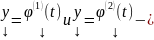некоторые решения (1), то чисел также является решением (1)

Док-во: Введем в ЛП столбцов функций оператор L: 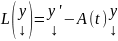, тогда систему (1) можно переписать в виде (3) . Пусть и решения, т.е. 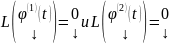. Тогда . Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.

Замеч. Из 1) и 2) следует, что совокупность всевозможных решений ОСЛОДУ (1) образует ЛП, которое обозначим

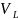
3. (О нуле решения) Если 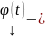решение (1) или (3) с непрерывными коэффициентами

Док-во: Рассмотрим ЗК для (1) : 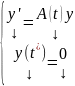С одной стороны 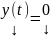является ее решением, с другой стороны тоже ее решение. Но по ТСЕ на всем 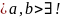Решение ЗК

4. (О линейной зависимости)

Пусть решение (1) (или (3)) . Тогда эта система решения является ЛЗ

Док-во: Рассмотрим эту систему при . При фиксированном это просто набор из столбца высоты оскольку ЛП столбцов чисел высоты имеет размерность , то система 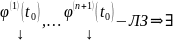нетривиальный набор 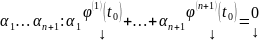(4). Рассмотрим 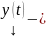ЛК решений (1) является решением (2), причем в соответствии с (4). Таким образом 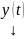является решением ЗК , но эта ЗК также обладает решением

По ТСЕ получаем

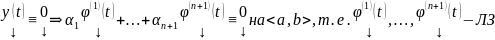
5. (О линейной независимости)

ОСЛОДУ (1) (или (3)) с непрерывными коэффициентами обладает n ЛНЗ решениями

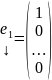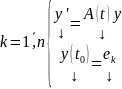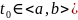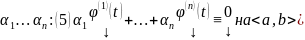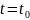
Док-во: Рассмотрим набор столбцов : , и рассмотрим n штук ЗК : где . Пусть решения этих ЗК соответственно. Предположим, что эта система решений ЛЗ. Тогда нетривиальный набор . Тогда (5) должно быть выполнено и при т.е. т.е. т.е. 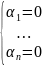. Противоречие тому, что набор 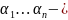нетривиально. Оно вызвано из предположения что ЛЗ эта система ЛНЗ на .

Сл. Из 4 и 5 получаем, что (отсюда любой базис содержит ровно элементов)

Вопрос 15.

1. ОСЛОДУ

(3)

Опр. Любой базис в назовем фундаментальной системой решений (ФСР) : ОСЛОДУ (1) (или(3)). Т.е. ФСР это упорядоченный набор из n ЛНЗ решений ОСЛОДУ (и всякое решение может быть передано как ЛК элементов этого набора)

6. (Об общем решении ОСЛОДУ)

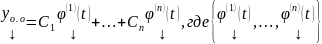назовем ФСР ОСЛОДУ, произвольные постоянные

Док-во: Поскольку 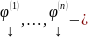базис, то любое решение является ЛК

Из свойства линейности любая ЛК 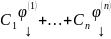является решением.

Вопрос 16.

1. ОСЛОДУ

(3)

Матрица решений и определитель Вронского.

Пусть произвольные решения (1) (или(3)). Запишем из по столбцам в матрицу

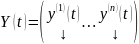
Опр. называется матрицей п=решений ОСЛОДУ (1). Поскольку , то матрица решений формально тоже удовлетворяет ОСЛОДУ (1), т.е.

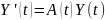
Опр. Матрица решений построена на ФСР ОСЛАДУ (1), т.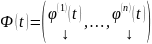е. , где 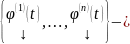произвольная ФСР ОСЛОДУ (1), назовем фундаментальной матрицей решений (ФМР)

Опр. Рассмотрим . назовем определителем Вронского (вронскианом) системы решений

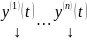
Замеч. определитель Вронского можно рассматривать для любой системы n столбцов функций высоты n , т.е. не обязательно для решений ОСЛОДУ.

Свойства МР и ОВ.

1. Пусть ЛЗ на системы столбцов функций высоты n (не обязательно решений ОСЛОДУ). Тогда на

Док-во: Система ЛЗ нетривиальный набор на . При любом фиксированном (6) представляет собой ОСЛАУ относительно .Поскольку у нее имеется нетривиальное решение, то определитель этой системы =0. Но определитель этой ОСЛАУ это 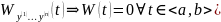, т.е.

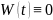
2. Пусть система решений ОСЛОДУ (1) с непрерывными коэффициентами и 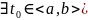: . Тогда ЛЗ на ( соот на )

Док-во: Рассмотрим ОСЛАУ относительно

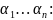
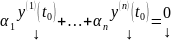
Поскольку ее определитель есть 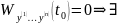нетривиальное решение. Пусть это 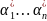. Рассмотрим тогда 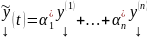это ЛК решений ОСЛОДУ (1), т.е. тоже решение, причем оно является решением ЗК Но эта ЗК обладает тривиальным решением по ТСЕ Т.о. то нетривиальный набор на

Замеч. Если 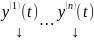не является решениями ОСЛОДУ (1) с непрерывными коэффициентами то это свойство не обязано выполнятся

3. Пусть ФМР для ОСЛОДУ (1) , то 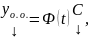где 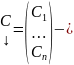столбец произвольных постоянных

Док-во:

4. Если Ф(t) – ФМР ОСЛОДУ (1), то с непрерывными коэффициентами ЗК 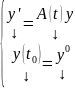имеет решение

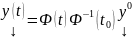
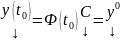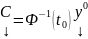Док-во: решению ЗК соответствует конкретный набор произвольных постоянных. Найдем его. Имеем Поскольку (т.к. ЛНЗ) Тогда Тогда решение ЗК есть

5. Если ФСР ОСЛОДУ , то , где след матрицы A(t)

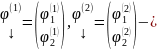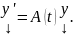Док-во: Докажем для n=2. Пусть ФСР ОСЛОДУ Тогда k=1,2 получим, что (10) . Тогда удовлетворяет ОДУ