Комплексозначные решения ослоду с действительными коэффициентами.

Если имеет комплексозначные коэффициенты, все свойства решений, матрицы решений и ОВ сохраняются.

Рассмотрим теперь систему с действительными коэффициентами. Она может обладать комплексозначными решениями.

Теор. Если , где столбцы действительных функций является решениемм ОСЛОДУ с действительными коэффициентами . 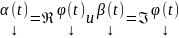также является решениями этой ОСЛОДУ

Док-во: Приравнивая действительные и мнимые части 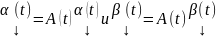. Более того, поскольку является ЛК решений, 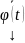также является решением этой системы.

Все ТСЕ

Теор1.

Теор2.(ТСЕ решение ЗК уравнения 1-го порядка, не разрешенных относительно производной)

некоторая точка

Пусть

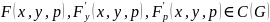
. Тогда Решение уравнения (3) н.у. (2) при этом дополнительно выполняется, что

Теор3. ТСЕ решние ЗК для нормальной СОДУ

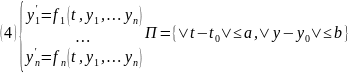Если , то Решение нормальной СОДУ (4) удовлетворяющее н.у.

Теор4. ТСЕ решения ЗК для нормальной СЛОДУ

Если , то и любого набора начальных условий (5) Решение ЗК (6) (5) на всем

Теор5. ТСЕ решения ЗК для уравнения n-го порядка, разрешенного относительно старшей производной

определена в G внутренняя точка в G. Если 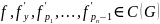, то Решение уравнения (7), удовлетворяющее начальным условиям

Теор6. ТСЕ для ЛОДУ n-го порядка

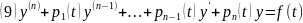. Если , то и любого набора начальных условий (8) Решение ЗК (9) (8) на всем