
- •Вопрос 1. Основные определения.
- •Вопрос 2.
- •Вопрос 3. Решение оду 1-го порядка в простейших случаях.
- •Уравнения с разделяющимися переменными
- •Однородные уравнения.
- •Вопрос 4.
- •Уравнение Бернулли
- •Уравнение Риккати
- •Вопрос 5. Уравнение в полных дифференциалах
- •Практический способ отыскания
- •Интегрирующий множитель
- •Вопрос 6. Уравнения 1-го порядка, не разрешенные относительно производной
- •Маленькое дополнение
- •Вопрос 7. Метод введения параметра
- •Частный случай
- •Вопрос 8
- •Вопрос 9 Уравнение Лагранжа и уравнение Клеро
- •Вопрос 10 Уравнения высших порядков, интегрируемые в квадратурах или допускающие понижения порядка.
- •Вопрос 11
- •Вопрос 12. Нормальные системы оду 1-го порядка.
- •Линейные нормальные системы.
- •Вопрос 13
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 17
- •Вопрос 18 Неоднородные слоду
- •Вопрос 19
- •Вопрос 20. Глава. Линейные системы с постоянными коэффициентами. Фср ослоду с постоянными коэффициентами.
- •Вопрос 21.
- •Вопрос 22. Замечания о построении фср в случае кратных корней
- •Вопрос 23.
- •Вопрос 24. Глава. Линейные оду высокого порядка (лоду вп) Определение лоду вп, сведение к нормальной слоду
- •Вопрос 25
- •Вопрос 26. Однородные лоду вп
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29. Неоднородные лоду вп. Метод вариации произвольных постоянных.
- •Вопрос 30.
- •Вопрос 31. Глава. Лоду вп с постоянными коэффициентами Однородные лоду вп с постоянными коэффициентами
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •Вопрос 36. Тсе решение зк для уравнения 1-го порядка, разрешенного относительно производной. До-во существования решения
- •Вопрос 37.
- •Глава. Элементы вариационного исчисления Основные понятия
- •Вопрос 39.
- •Вопрос 40
- •Вопрос 40.
- •Рассмотрим важные частные случаи
- •Вопрос 41.
- •Вопрос 42.
- •Вопрос 43.
- •Комплексозначные решения ослоду с действительными коэффициентами.
Вопрос 35.
Напомним, что
В случае произвольной ищем методом вариации произвольных постоянных. Однако в случае специального вида удобнее применять метод неопределенных коэффициентов
Теор. (принцип суперпозиции)
Если является решением уравнения , то является решением уравнения
Док-во: #
Пусть многочлен степени с определенными коэффициентами, произвольная(комплексная)
В силу принципа суперпозиции рассмотрим поиск для
Возможны 2 случая :
нерезонансный случай
резонансный случай
Резонансный случай.
Пусть
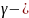 корень
характеристического уравнения кратности
k :
корень
характеристического уравнения кратности
k :

Теор.
Если
,
то
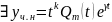 ,
где
многочлен
той же степени, что и
и его коэффициенты по данным коэффициентам
определяются единственным образом.
,
где
многочлен
той же степени, что и
и его коэффициенты по данным коэффициентам
определяются единственным образом.
Док-во:
Используя диф тождество, подставим
 в уравнение
,
получим :
в уравнение
,
получим :
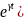 .
Рассмотрим ЛО
.
Рассмотрим ЛО
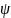 ,
действующего в ЛП многочлена степени
.
,
действующего в ЛП многочлена степени
.
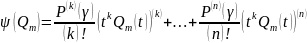 .
Тогда
.
Тогда
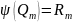 .
Покажем, что
.
Покажем, что
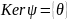 .
От противного. Пусть
.
От противного. Пусть
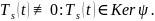 Тогда
Тогда
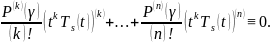 Если
Если
 ,
получим
,
получим
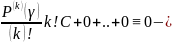 невозможно. Если же
,
первое слагаемое многочлена степени s
, а остальные слагаемые имеют степень
< s, т.к. там берутся более
высшие производные
невозможно чтобы сумма = 0. Пришли к
противоречию
невозможно. Если же
,
первое слагаемое многочлена степени s
, а остальные слагаемые имеют степень
< s, т.к. там берутся более
высшие производные
невозможно чтобы сумма = 0. Пришли к
противоречию
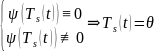 ,
т.е. нулевой многочлен. Таким образом
,
т.е. нулевой многочлен. Таким образом
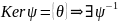 Он определяется единственным образом.
Он определяется единственным образом.
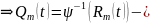 определяется
единственным образом
определяется
единственным образом
Замеч.
На практике
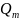 отыскивают подставляя
отыскивают подставляя
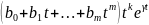 в уравнение
,
сокращая
и приравнивая коэффициенты при одинаковых
степенях t. Получают СЛАУ
из
в уравнение
,
сокращая
и приравнивая коэффициенты при одинаковых
степенях t. Получают СЛАУ
из
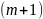 неизвестных. Из док-ва теоремы получаем,
что она имеет единственное решение.
неизвестных. Из док-ва теоремы получаем,
что она имеет единственное решение.
Если уравнение
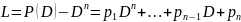 имеет действительные коэффициенты
имеет действительные коэффициенты
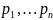 ,
а
,
а
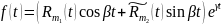 ,
где
,
где
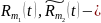 многочлены
степеней
с действительными коэффициентами,
многочлены
степеней
с действительными коэффициентами,
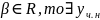 в виде
в виде
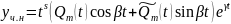 ,
где
,
где
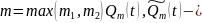 многочлены
степени m с действительными
коэффициентами
многочлены
степени m с действительными
коэффициентами
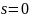 ,
если
,
если
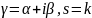 ,
если
,
если
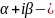 корень кратности k
корень кратности k
Вопрос 36. Тсе решение зк для уравнения 1-го порядка, разрешенного относительно производной. До-во существования решения
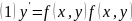 определена в
определена в
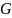
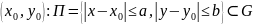
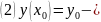 начальные
условия
начальные
условия
ЗК. Найти
интегральную кривую уравнения (1)
проходящую через
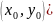 найти
решение (1), удовлетворяющее н.у. (2))
найти
решение (1), удовлетворяющее н.у. (2))
Теор.
Пусть
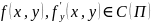 .
Тогда
.
Тогда
 в
в
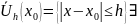 решение уравнения (1) удовлетворяющее
н.у. (2) и это решение единственное на
решение уравнения (1) удовлетворяющее
н.у. (2) и это решение единственное на
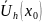
Док-во: Поэтапное доказательство существования решения
Докажем, что удовлетворяет в П условию Липшица по переменной , т.е.
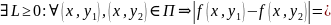 теор.
о конечных приращениях
теор.
о конечных приращениях
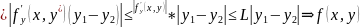 удовлетворяет условию Л в П
удовлетворяет условию Л в П
Докажем, что ЗК (1), (2) эквивалентна интегральному уравнению
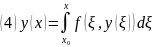
##
Пусть
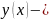 решение
ЗК (1), (2). Тогда
решение
ЗК (1), (2). Тогда
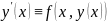 .
Проинтегрируем это тождество от
до
.
Проинтегрируем это тождество от
до
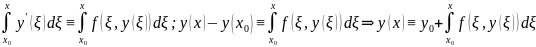
Пусть
решение
(4). Тогда
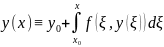 Дифференцируем по
,
получим :
Дифференцируем по
,
получим :
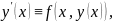 причем
причем
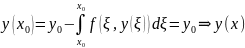 является решением ЗК (1), (2)##
является решением ЗК (1), (2)##
(Построение функциональной последовательности) Строим функциональную последовательность следующим образом. Везде считаем, что
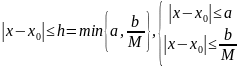
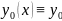
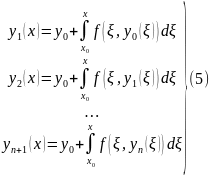
(Принадлежность П)
Покажем,
что при
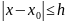 выполняется, что
выполняется, что
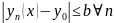 т.е.
т.е.
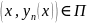
##
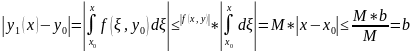
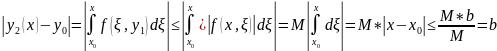
……
 ##
##
(Абсолютная и равномерная сходимость функциональной последовательности)
Покажем,
что
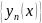 сходится абсолютно и равномерно на
сходится абсолютно и равномерно на
##
Очевидно
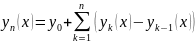 Таким образом, сходимость последовательности
Таким образом, сходимость последовательности
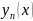 эквивалента сходимости функционального
ряда
эквивалента сходимости функционального
ряда
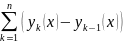 (т.к.
(т.к.
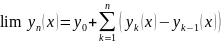 Рассмотрим
Рассмотрим
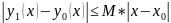 .
Тогда
.
Тогда
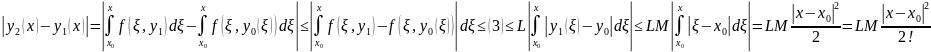
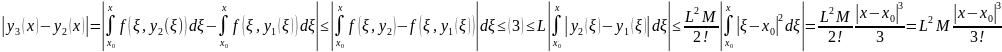
……
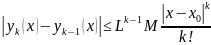
Тогда
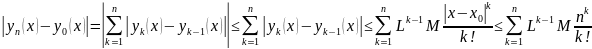 Числовой ряд
Числовой ряд
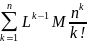 Сходится по признаку Даламбера
Сходится по признаку Даламбера
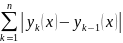 мажорируется сход числовым рядом
мажорируется сход числовым рядом
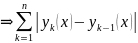 сходится абсолютно и равномерно на
по правилу Вейерштрассе.
сходится абсолютно и равномерно на
по правилу Вейерштрассе.
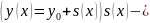 сумма
ряда.
сумма
ряда.
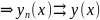 причем
непрерывна при
в случае равномерной сходимости.
причем
непрерывна при
в случае равномерной сходимости.
Замеч.
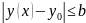 в силу теоремы о предельном преходе в
неравенствах
в силу теоремы о предельном преходе в
неравенствах
(Равномерная сходимость
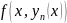 )
)
Покажем, что

##
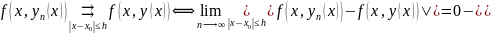 критерий
сходимости функциональной последовательности.
Рассмотрим
критерий
сходимости функциональной последовательности.
Рассмотрим
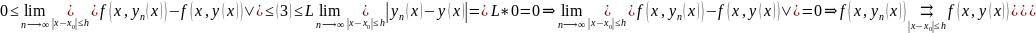 ##
##
(Решение интегрального уравнения)
Покажем, что
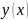 является решением интегрального
уравнения (4)
является решением интегрального
уравнения (4)
##
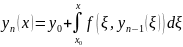 (из (5))
(из (5))
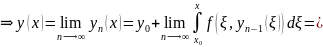 в
силу равномерной сходимости
в
силу равномерной сходимости
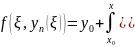 Но поскольку интегрируемое уравнение
(4) эквивалентно ЗК (1), (2) то
и является решенной ЗК ##
Но поскольку интегрируемое уравнение
(4) эквивалентно ЗК (1), (2) то
и является решенной ЗК ##
Таким образом доказано, что решение ЗК
Доказательство
конструктивное. Указан метод построения
решения. (Метод последовательного
приближения
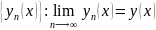 #
#
