Вопрос 33.

(В) Случай кратных корней характеристического уравнения

Теор. Пусть 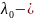корень кратности k характеристического уравнения, т.е.

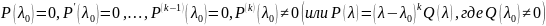. Тогда является решением ОЛОДУ ВП отвечающим значению

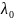
Перед доказательством этой теоремы рассмотрим.

Лемма. (Дифференциальное тождество)

Пусть 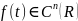. Тогда

Док-во: Рассмотрим формула Лейбница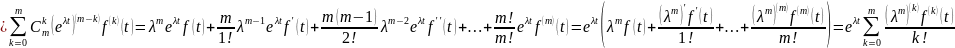 . Тогда

Докажем теперь теорему.

Док-во: берем . Тогда поскольку корень кратности 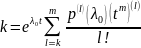, но при

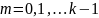
Лемма. Если произвольный многочлен степени m, то 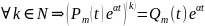, где многочлен той же степени.

Док-во: Методом математической индукции

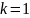
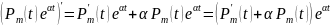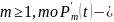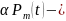БАЗА. Если многочлен степени (m-1), а многочлен степени m, в сумме будет многочлен степени m. Если же , то

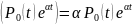
ШАГ. Пусть утверждение верно для , т.е. Покажем, что тогда она верна и для (см базу) – верно утверждение верно #

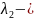Пусть теперь характеристическое уравнение имеет корни : кратности 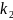кратности ,…, кратности 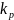различны, 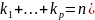. Тогда рассмотрим сумму h функций (решений ОЛОДУ ВП)

…

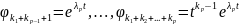Покажем, что эта система ЛНЗ (тогда это и будет ФСР). От противного. Предположим, что она ЛЗ, что нетривиальный набор чисел 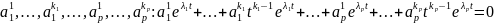. Поскольку набор чисел нетривиальный, то хотя бы один из многочленов 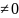. БОО считаем, что На самом деле, не только он, т.к если бы все остальные многочлены , то мы бы получили тождество : 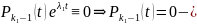противоречие есть еще какой-то ненулевой многочлен. Тогда 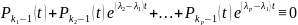Дифференцируем это тождество k раз по лемме Какой-то многочлен из 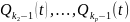будет 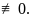БОО это 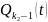. По тем же соображениям, что и выше не только он 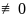, но и еще по крайней мере один другой. Умножаем обе части на 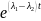, получим Дифференцируем еще раз. Далее используем те же соображения дойдем до того, что . С одной стороны из рассуждений, приведенных выше, получаем, что С другой стороны тождество (10) может быть выполнено только при 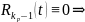противоречие. 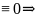Оно возникло из предположения, что нетривиальная ЛК построенных функций, которое Значит, предположение неверно только тривиальная ЛК построеная система функций ЛНЗ она представляет собой ФСР (вообще говоря значную). Для уравнения с вещественными коэффициентами из нее можно построить вещественную ФСР по тем же правилам что и в случае простых костей. #

Вопрос 34.

Неоднородные ЛОДУ ВП с постоянными коэффициентами.

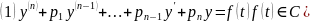
Напомним, что

В случае произвольной 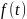ищем методом вариации произвольных постоянных. Однако в случае специального вида удобнее применять метод неопределенных коэффициентов

Теор. (принцип суперпозиции)

Если является решением уравнения 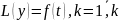, то является решением уравнения

Док-во: #

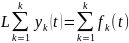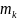Пусть многочлен степени с определенными коэффициентами, 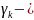произвольная(комплексная)

В силу принципа суперпозиции рассмотрим поиск для

Возможны 2 случая :

1. нерезонансный случай

2. резонансный случай

Нерезонансный случай

Пусть не является корнем характеристического уравнения :

Теор. Если 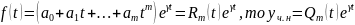. Где многочлен той же степени, что и 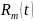, коэффициенты которого определяются единственным образом

Док-во: Подставим в уравнение 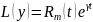используя диф тождество : . Тогда Рассмотрим ЛО, действующую ЛП многочленов степени Тогда (2) примет вид . Покажем, что т.е. ядро состоит только из многочлена От противного. Предположим, что . Тогда многочлен 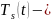многочлен степени s : 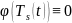. Но 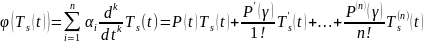. Тогда если s=0, т.е. , то первое слагаемое , а остальные невозмодно, чтобы 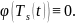Если же , то первое слагаемое будет многочленом степени s , а остальные слагаемы е имеют степень <s невозможно, чтобы сумма Мы пришли к противоречию : Таким образом получаем, что . Таким образом . Тогда обратим, т.е. 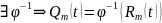, т.е. по заданному многочлену многочлен 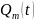определяется единственным образом

Замеч. На практике полагают, что , подставляем в уравнение , получают точку, сокращают обе части на и приравнивают коэффициенты при степени t , получа.т СЛАУ из уравнений с неизвестными