
- •Вопрос 1. Основные определения.
- •Вопрос 2.
- •Вопрос 3. Решение оду 1-го порядка в простейших случаях.
- •Уравнения с разделяющимися переменными
- •Однородные уравнения.
- •Вопрос 4.
- •Уравнение Бернулли
- •Уравнение Риккати
- •Вопрос 5. Уравнение в полных дифференциалах
- •Практический способ отыскания
- •Интегрирующий множитель
- •Вопрос 6. Уравнения 1-го порядка, не разрешенные относительно производной
- •Маленькое дополнение
- •Вопрос 7. Метод введения параметра
- •Частный случай
- •Вопрос 8
- •Вопрос 9 Уравнение Лагранжа и уравнение Клеро
- •Вопрос 10 Уравнения высших порядков, интегрируемые в квадратурах или допускающие понижения порядка.
- •Вопрос 11
- •Вопрос 12. Нормальные системы оду 1-го порядка.
- •Линейные нормальные системы.
- •Вопрос 13
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 17
- •Вопрос 18 Неоднородные слоду
- •Вопрос 19
- •Вопрос 20. Глава. Линейные системы с постоянными коэффициентами. Фср ослоду с постоянными коэффициентами.
- •Вопрос 21.
- •Вопрос 22. Замечания о построении фср в случае кратных корней
- •Вопрос 23.
- •Вопрос 24. Глава. Линейные оду высокого порядка (лоду вп) Определение лоду вп, сведение к нормальной слоду
- •Вопрос 25
- •Вопрос 26. Однородные лоду вп
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29. Неоднородные лоду вп. Метод вариации произвольных постоянных.
- •Вопрос 30.
- •Вопрос 31. Глава. Лоду вп с постоянными коэффициентами Однородные лоду вп с постоянными коэффициентами
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •Вопрос 36. Тсе решение зк для уравнения 1-го порядка, разрешенного относительно производной. До-во существования решения
- •Вопрос 37.
- •Глава. Элементы вариационного исчисления Основные понятия
- •Вопрос 39.
- •Вопрос 40
- •Вопрос 40.
- •Рассмотрим важные частные случаи
- •Вопрос 41.
- •Вопрос 42.
- •Вопрос 43.
- •Комплексозначные решения ослоду с действительными коэффициентами.
Вопрос 29. Неоднородные лоду вп. Метод вариации произвольных постоянных.

Теор. (Об общем решении НЛОДУ ВП)

Док-во: Приведем (1) к виду (2)
Пусть

Получили
неоднородное СЛОДУ .
Покажем, что
справедливо для (2).
.
Покажем, что
справедливо для (2).
Покажем, что решение. . Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть произвольное решение (1). Рассмотрим разность . Покажем, что эта разность удовлетворяет (2). . Пусть какая-нибудь ФСР ОСЛОДУ (2), тогда любое решение СЛОДУ (1) может быть представлено в виде при некоторых значениях
Вопрос 30.
Будем искать ч.н. методом вариации произвольных постоянных
Пусть
произвольная
ФСР ОЛОДУ. Тогда
 ,
где
,
где
 строка
элементов ФСР,
столбец
произвольных постоянных.
строка
элементов ФСР,
столбец
произвольных постоянных.
Будем искать
 в виде
в виде
 ,
где
,
где
 столбец
неизвестных пока функций. Тогда
столбец
неизвестных пока функций. Тогда
 ,
наложим условия, что
,
наложим условия, что
 Тогда
Тогда

 ,
наложим условия
,
наложим условия
 .
Тогда
.
Тогда
 и т.д. На каждом шаге полагаем, что
и т.д. На каждом шаге полагаем, что
 .
.
Тогда
 Поскольку
Поскольку
 ,
тогда
,
тогда
 .
С другой стороны, поскольку y
является решением неоднородного
уравнения (1), то
.
С другой стороны, поскольку y
является решением неоднородного
уравнения (1), то
 Подставим (3) и (4) в (2) получим :
Подставим (3) и (4) в (2) получим :
 (
( ,
но
,
но
 Поэтому после сокращения в (5) :
Поэтому после сокращения в (5) : Следовательно, столбец
Следовательно, столбец
 удовлетворяет случ СЛАУ
удовлетворяет случ СЛАУ
 Запишем в развернутой форме
Запишем в развернутой форме

 Поскольку
Поскольку
 ,
то
решение
,
то
решение
 Интегрируя, получаем :
Интегрируя, получаем :

 Тогда (7)
Тогда (7)
 Придавая константам
произвольным значениям например, ноль
,
получим :
Придавая константам
произвольным значениям например, ноль
,
получим : Тогда (7) может быть представлено в виде
Тогда (7) может быть представлено в виде
 это будет
это будет
 .
Таким образом, (7) дает при всевозможных
общее решение неоднородного ОЛОДУ ВП.
.
Таким образом, (7) дает при всевозможных
общее решение неоднородного ОЛОДУ ВП.
Вопрос 31. Глава. Лоду вп с постоянными коэффициентами Однородные лоду вп с постоянными коэффициентами

Рассмотрим
ЛП
 ЛП
функций, непрерывные с производной до
n-го порядка включительно
на
.
Пусть в это ЛП действ ЛО
ЛП
функций, непрерывные с производной до
n-го порядка включительно
на
.
Пусть в это ЛП действ ЛО
 ,
т.е.
,
т.е.

Далее получаем,
что

Тогда

Рассмотрим
многочлен n-ой степени :
 Ему сопоставим ЛО
Ему сопоставим ЛО
 Тогда (1) можно переписать в виде :
Тогда (1) можно переписать в виде :

Будем искать
решение (1) ( или что то же (2)) в виде
 .
Подставим во (2)
.
Подставим во (2)

Видим, что
 будет решением (1) (или(2))
является корнем уравнения
будет решением (1) (или(2))
является корнем уравнения

Опр.
называется характеристическим
многочленом уравнения (1)( или (2)), а
уравнение
 характеристическим
уравнением.
характеристическим
уравнением.
Теор.
является решением ОСЛОДУ ВП (1) ((2))
 корень
характеристического уравнения
корень
характеристического уравнения
Док-во:

Способы построения ФСР
(А) Построение ФСР ОЛОДУ ВП в случае, когда все корни характеристического многочлена различны.
Пусть
 различные
корни характеристического многочлена.
Тогда имеется n решений
:
различные
корни характеристического многочлена.
Тогда имеется n решений
:
 Покажем, что они образуют ФСР, т.е.
являются ЛНЗ
Покажем, что они образуют ФСР, т.е.
являются ЛНЗ
Док-во:
Рассмотрим

 далее
из каждой строки начиная с последней
вычитаем предыдущую строку умноженную
на
далее
из каждой строки начиная с последней
вычитаем предыдущую строку умноженную
на

 по
индукции
по
индукции
Отсюда видно,
что если все
 различны, то
различны, то
 ЛНЗ
на
ФСР
ЛНЗ
на
ФСР
Вопрос 32.
(Б) Построение действительных ФСР для ОСЛОДУ ВП с действительными коэффициентами в случае простых корней характеристического уравнения при наличии комплексных
Замеч.
ФСР, построенная в пункте (А) может быть
как П-, так и
 значной.
Если само уравнение имеет комплексные
коэффициенты, то комплекснозначная ФСР
дает произвольные комплекснозначное
решение такого уравнения. Но допустим,
что
значной.
Если само уравнение имеет комплексные
коэффициенты, то комплекснозначная ФСР
дает произвольные комплекснозначное
решение такого уравнения. Но допустим,
что
 и нас интересуют только вещественные
решения. В этом случае, если среди корней
характеристического уравнения имеются
комплекные, мы имеем комплекснозначную
ФСР и представление произвольного
вещественного решения через нее
затруднительно. Поэтому представляет
интерес построение вещественной ФСР.
и нас интересуют только вещественные
решения. В этом случае, если среди корней
характеристического уравнения имеются
комплекные, мы имеем комплекснозначную
ФСР и представление произвольного
вещественного решения через нее
затруднительно. Поэтому представляет
интерес построение вещественной ФСР.
Пусть все
корни характеристического уравнения
различны, но имеются комплексные. Тогда
если
 корень
характеристического уравнения, то
корень
характеристического уравнения, то
 тоже
корень, поскольку
тоже
корень, поскольку

Упорядочим
корни следующим образом :


Соответственно комплексозначная ФСР будет :



Тогда
 базис
в ЛП решений. Перейдем к системе функций
:
базис
в ЛП решений. Перейдем к системе функций
:



Матрица
перехода
 будет иметь вид :
будет иметь вид :

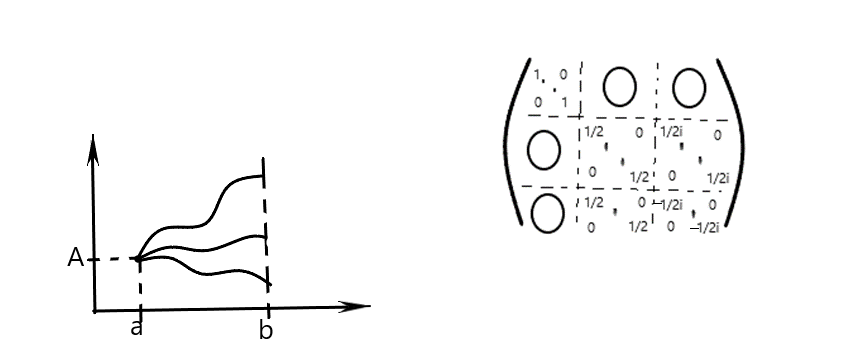


 ЛНЗ
базис
ЛНЗ
базис
Но это будет
уже вещественный базис, т.к.
 ,
,
 вещественная
вещественная




