
- •Вопрос 1. Основные определения.
- •Вопрос 2.
- •Вопрос 3. Решение оду 1-го порядка в простейших случаях.
- •Уравнения с разделяющимися переменными
- •Однородные уравнения.
- •Вопрос 4.
- •Уравнение Бернулли
- •Уравнение Риккати
- •Вопрос 5. Уравнение в полных дифференциалах
- •Практический способ отыскания
- •Интегрирующий множитель
- •Вопрос 6. Уравнения 1-го порядка, не разрешенные относительно производной
- •Маленькое дополнение
- •Вопрос 7. Метод введения параметра
- •Частный случай
- •Вопрос 8
- •Вопрос 9 Уравнение Лагранжа и уравнение Клеро
- •Вопрос 10 Уравнения высших порядков, интегрируемые в квадратурах или допускающие понижения порядка.
- •Вопрос 11
- •Вопрос 12. Нормальные системы оду 1-го порядка.
- •Линейные нормальные системы.
- •Вопрос 13
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 17
- •Вопрос 18 Неоднородные слоду
- •Вопрос 19
- •Вопрос 20. Глава. Линейные системы с постоянными коэффициентами. Фср ослоду с постоянными коэффициентами.
- •Вопрос 21.
- •Вопрос 22. Замечания о построении фср в случае кратных корней
- •Вопрос 23.
- •Вопрос 24. Глава. Линейные оду высокого порядка (лоду вп) Определение лоду вп, сведение к нормальной слоду
- •Вопрос 25
- •Вопрос 26. Однородные лоду вп
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29. Неоднородные лоду вп. Метод вариации произвольных постоянных.
- •Вопрос 30.
- •Вопрос 31. Глава. Лоду вп с постоянными коэффициентами Однородные лоду вп с постоянными коэффициентами
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •Вопрос 36. Тсе решение зк для уравнения 1-го порядка, разрешенного относительно производной. До-во существования решения
- •Вопрос 37.
- •Глава. Элементы вариационного исчисления Основные понятия
- •Вопрос 39.
- •Вопрос 40
- •Вопрос 40.
- •Рассмотрим важные частные случаи
- •Вопрос 41.
- •Вопрос 42.
- •Вопрос 43.
- •Комплексозначные решения ослоду с действительными коэффициентами.
Вопрос 26. Однородные лоду вп
Свойства:
Обладает тривиальным решением
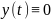
Док-во: очевидно
(Линейность)
Если
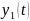 и
и
 решения
(1), то
решения
(1), то
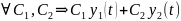 также является решением (1) (можно
распространить на любое количество
решений)
также является решением (1) (можно
распространить на любое количество
решений)
Сл. Совокупность всевозможных решений (1) образует ЛП, которое будем называть ЛП решений ЛОДУ ВП
Опр.
Совокупность функций
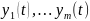 называется ЛЗ на
,
если
нетривиальный набор чисел
называется ЛЗ на
,
если
нетривиальный набор чисел
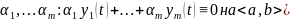 .
Если же это возможно только когда
.
Если же это возможно только когда
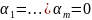 ,
то совокупность функций называется
ЛНЗ.
,
то совокупность функций называется
ЛНЗ.
Уравнение (1) обладает n ЛНЗ решениями
Док-во:
Рассмотрим n решений
уравнения (1).
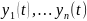 ,
являются решениями ЗК для (1) с начальными
условиями соответственно
,
являются решениями ЗК для (1) с начальными
условиями соответственно
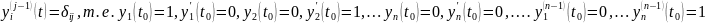 Покажем, что эти решения ЛНЗ. Пусть
Покажем, что эти решения ЛНЗ. Пусть
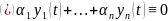 Продифференцируем это тождество (n-1)
раз, получим :
Продифференцируем это тождество (n-1)
раз, получим :
 Полагая в (4)
получим
Полагая в (4)
получим
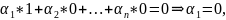
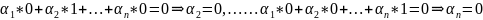 .
Таким образом,
.
Таким образом,
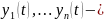 ЛНЗ
ЛНЗ
Любая система из (n+1) решения (1) будет ЛЗ
Док-во:
Рассмотрим
решение
(1). Пусть
.
Составим ОСЛАУ
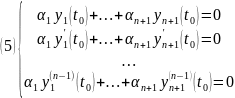 Число уравнений
Число уравнений
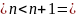 число неизвестных
эта ОСЛАУ обладает нетривиальным
решением. Пусть это
число неизвестных
эта ОСЛАУ обладает нетривиальным
решением. Пусть это
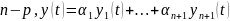 Это ЛК решений
(по
св-ву 2)
это
тоже решение (1). В силу (5) оно удовлетворяет
следующему НУ :
Это ЛК решений
(по
св-ву 2)
это
тоже решение (1). В силу (5) оно удовлетворяет
следующему НУ :
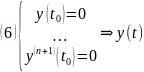 является решением ЗК (1) (6). Но эта ЗК
также имеет тривиальное решение. По ТСЕ
имеем
является решением ЗК (1) (6). Но эта ЗК
также имеет тривиальное решение. По ТСЕ
имеем
 нетривиальный
набор) на
нетривиальный
набор) на
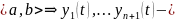 ЛЗ на
ЛЗ на
Сл. ЛП решений ЛОДУ ВП (1) имеет размерность = n, и соответственно любые n ЛНЗ решений могут быть его базисом
Вопрос 27.
Опр. Упорядоченный набор n ЛНЗ ЛОДУ ВП (1) называется его фундаментальной системой решений (ФСР)
Пусть
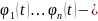 произвольная
ФСР в ЛП решений (1), то общее решение
(1) имеет вид
произвольная
ФСР в ЛП решений (1), то общее решение
(1) имеет вид
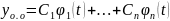 ,
где
,
где
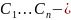 произвольные
постоянные
произвольные
постоянные
Док-во: следует из того, что ФСР базис
Рассмотрим
на
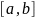 линейное однородное дифференциальное
уравнение
линейное однородное дифференциальное
уравнение
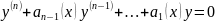 .
Общим решением этого уравнения на
отрезке
называется функция
.
Общим решением этого уравнения на
отрезке
называется функция
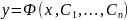 ,
зависящая от n произвольных
постоянных
,
зависящая от n произвольных
постоянных
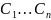 и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям:
при любых допустимых значениях постоянных , функция является решением уравнения на
какова бы ни была начальная точка
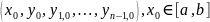 ,
существуют такие значения
,
существуют такие значения
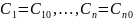 ,
что функция
,
что функция
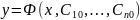 удовлетворяет начальным условиям
удовлетворяет начальным условиям
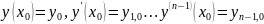
Вопрос 28.
Опр.
Пусть
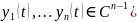 набор функций (не обязательно решение
(1)). Тогда
набор функций (не обязательно решение
(1)). Тогда
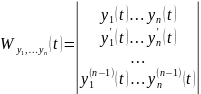 называется определителем Вронского
системы функций
называется определителем Вронского
системы функций
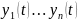
Формула Лиувилля
Если
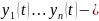 решение
ЛОДУ ВП (1), то
решение
ЛОДУ ВП (1), то
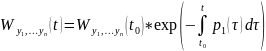
Док-во:
n=2 Пусть
 решения
(1), тогда
решения
(1), тогда
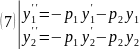
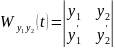
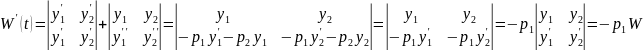 ,
т.е. получаем ОДУ
,
т.е. получаем ОДУ
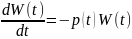 ,
,

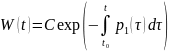 При
получим
При
получим
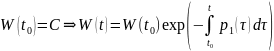
Сл.
Если
решение
ЛОДУ ВП (1) (с непрерывными коэффициентами
на
,
то либо
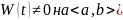 ,
либо
,
либо
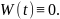
Если решение ЛОДУ ВП (1) с непрерывными коэффициентами на и в некоторой
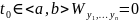 ,
то
ЛЗ
на
,
то
ЛЗ
на
Док-во:
Пусть
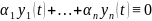 .
Дифференцируем
.
Дифференцируем
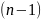 раз, получим
раз, получим
 При
При
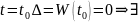 нетривиальное решение
.
Рассмотрим
нетривиальное решение
.
Рассмотрим
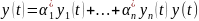 является решением ЗК для (1) с нетривиальным
НУ. Эта ЗК также имеет тривиальное
решение
является решением ЗК для (1) с нетривиальным
НУ. Эта ЗК также имеет тривиальное
решение
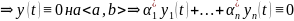 на
на
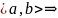 ЛЗ
ЛЗ
Замеч. Это свойство не выполняется для произв (n-1) раз дифф функций на
Свойство
Если
произвольная
система ЛЗ функций на
,
то
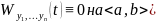
Док-во:
Пусть
нетривиальный набор
.
Тогда
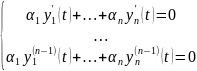 Поскольку
эта СЛАУ обладает нетривиальным
решением, то
Поскольку
эта СЛАУ обладает нетривиальным
решением, то
(О построении уравнения по ФСР)
Система
функций
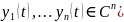 образует ФСР некоторого ЛОДУ n-го
порядка с непрерывными на
коэффициентами
образует ФСР некоторого ЛОДУ n-го
порядка с непрерывными на
коэффициентами
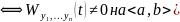
Док-во:
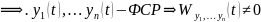
Пусть
теперь
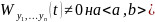 .
Рассмотрим
.
Рассмотрим
 .
Очевидно
решение
этого уравнения(т.к. при подстановке
дают два одинаковых столбца). Раскрывая
по последнему столбцу, получим :
.
Очевидно
решение
этого уравнения(т.к. при подстановке
дают два одинаковых столбца). Раскрывая
по последнему столбцу, получим :
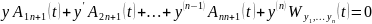 .
Соотв алгебраические коэффициенты
выражены через известные функции и
.
Соотв алгебраические коэффициенты
выражены через известные функции и
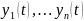 и их производные до n
порядка включительно
определены и непрерывны на
.
Тогда
и их производные до n
порядка включительно
определены и непрерывны на
.
Тогда
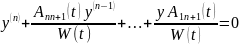 Получим искомое уравнение, примем
его ФСР.
Получим искомое уравнение, примем
его ФСР.
Если
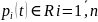 и
и
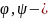 вещественные
функции
вещественные
функции
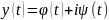 является комплексным решением уравнения
является комплексным решением уравнения
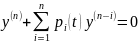 .
Тогда
.
Тогда
 также является решением и
также является решением и
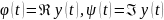 также является решением
также является решением

