- •Вопрос 1. Основные определения.
- •Вопрос 2.
- •Вопрос 3. Решение оду 1-го порядка в простейших случаях.
- •Уравнения с разделяющимися переменными
- •Однородные уравнения.
- •Вопрос 4.
- •Уравнение Бернулли
- •Уравнение Риккати
- •Вопрос 5. Уравнение в полных дифференциалах
- •Практический способ отыскания
- •Интегрирующий множитель
- •Вопрос 6. Уравнения 1-го порядка, не разрешенные относительно производной
- •Маленькое дополнение
- •Вопрос 7. Метод введения параметра
- •Частный случай
- •Вопрос 8
- •Вопрос 9 Уравнение Лагранжа и уравнение Клеро
- •Вопрос 10 Уравнения высших порядков, интегрируемые в квадратурах или допускающие понижения порядка.
- •Вопрос 11
- •Вопрос 12. Нормальные системы оду 1-го порядка.
- •Линейные нормальные системы.
- •Вопрос 13
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 17
- •Вопрос 18 Неоднородные слоду
- •Вопрос 19
- •Вопрос 20. Глава. Линейные системы с постоянными коэффициентами. Фср ослоду с постоянными коэффициентами.
- •Вопрос 21.
- •Вопрос 22. Замечания о построении фср в случае кратных корней
- •Вопрос 23.
- •Вопрос 24. Глава. Линейные оду высокого порядка (лоду вп) Определение лоду вп, сведение к нормальной слоду
- •Вопрос 25
- •Вопрос 26. Однородные лоду вп
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29. Неоднородные лоду вп. Метод вариации произвольных постоянных.
- •Вопрос 30.
- •Вопрос 31. Глава. Лоду вп с постоянными коэффициентами Однородные лоду вп с постоянными коэффициентами
- •Вопрос 32.
- •Вопрос 33.
- •Вопрос 34.
- •Вопрос 35.
- •Вопрос 36. Тсе решение зк для уравнения 1-го порядка, разрешенного относительно производной. До-во существования решения
- •Вопрос 37.
- •Глава. Элементы вариационного исчисления Основные понятия
- •Вопрос 39.
- •Вопрос 40
- •Вопрос 40.
- •Рассмотрим важные частные случаи
- •Вопрос 41.
- •Вопрос 42.
- •Вопрос 43.
- •Комплексозначные решения ослоду с действительными коэффициентами.
Вопрос 23.
Неоднородные СЛОДУ с постоянными коэффициентами.
постоянная матрица.
В общем случае
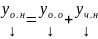 .
Если
ФСР
ОСЛОДУ (1)
ФМР.
Тогда
,
.
Если
ФСР
ОСЛОДУ (1)
ФМР.
Тогда
,
 ,
а
,
а
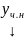 отыскиваем, полагая
отыскиваем, полагая
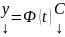 (метод вариации произвольных постоянных).
Однако в случае, когда
(метод вариации произвольных постоянных).
Однако в случае, когда
 имеет специальный вид, удобнее использовать
метод неопределенных коэффициентов.
имеет специальный вид, удобнее использовать
метод неопределенных коэффициентов.
Теор. (принцип суперпозиции)
Если
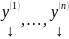 является решениями соответствующей
системы
является решениями соответствующей
системы
 ,
,
то
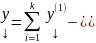 является
решением системы
является
решением системы
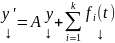
ДОКАЗАТЬ
Метод неопределенных коэффициентов.
Теор.
Если
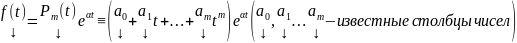 ,
,
то
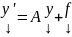 имеет r решений вида :
имеет r решений вида :

 .
.
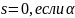 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
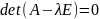 .
.
 являются корнем характеристического
уравнения
алгебраической кратности k.
Неизвестные столбцы могут быть найдены
путем подстановки решений вида (1) в
неоднородную СЛОДУ и приравнены
коэффициенты при степенях t
в правой и левой частях. (без доказательства)
являются корнем характеристического
уравнения
алгебраической кратности k.
Неизвестные столбцы могут быть найдены
путем подстановки решений вида (1) в
неоднородную СЛОДУ и приравнены
коэффициенты при степенях t
в правой и левой частях. (без доказательства)
Теор.
Если А – вещественная матрица, а
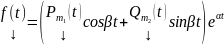 ,
где
,
где
 векторные
многочлены с действительными
коэффициентами,
векторные
многочлены с действительными
коэффициентами,
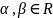 ,
тогда система
,
тогда система
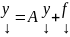 обладает частным решением такого вида
:
обладает частным решением такого вида
:
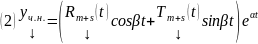 ,
где
,
где
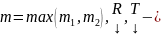 векторные
многочлены с действительными коэффициентами
векторные
многочлены с действительными коэффициентами
 соответственно. .
соответственно. .
 не является корнем характеристического
уравнения
.
не является корнем характеристического
уравнения
.
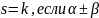 являются корнем характеристического
уравнения
алгебраической кратности k.
Коэффициенты многочленов R
и T определяются путем
подстановки решений вида (2) в неоднородную
СЛОДУ
и
приравнивая коэффициенты при
являются корнем характеристического
уравнения
алгебраической кратности k.
Коэффициенты многочленов R
и T определяются путем
подстановки решений вида (2) в неоднородную
СЛОДУ
и
приравнивая коэффициенты при
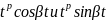 в обеих частях
в обеих частях
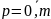 (без док-ва)
(без док-ва)
Вопрос 24. Глава. Линейные оду высокого порядка (лоду вп) Определение лоду вп, сведение к нормальной слоду
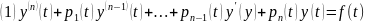
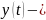 неизвестная
функция
неизвестная
функция
Называется ЛОДУ ВП,
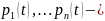 его
коэффициенты
его
коэффициенты
Будем считать,
что
 непрерывны
на рассмотренном интервале
непрерывны
на рассмотренном интервале
Если
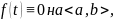 то
ЛОДУ ВП называется однородным, в противном
случае – неоднородным (противоположный
случай, когда f хотя бы в
одной точке отлична от 0)
то
ЛОДУ ВП называется однородным, в противном
случае – неоднородным (противоположный
случай, когда f хотя бы в
одной точке отлична от 0)
Опр.
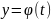 называется частным решением (1), если
называется частным решением (1), если
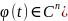 и при подстановке в (1) обращает его в
тождество
и при подстановке в (1) обращает его в
тождество
Опр. Совокупность всевозможных частных решений образует общее решение уравнения (1). Сведем (1) к нормальной системе
Пусть
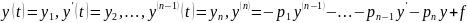
Тогда (2)
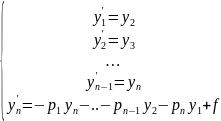
Всякое решение
(1) будет решением (2) и наоборот. Поэтому
(1) эквивалентна системе (2) и соответственно
его общее решение содержат и произвольных
постоянных. Пусть
 произвольный
набор чисел ЗК для (1) формулируется
следующим образом: найти решение
уравнения (1), удовлетворяющее дополнительным
условиям (3)
произвольный
набор чисел ЗК для (1) формулируется
следующим образом: найти решение
уравнения (1), удовлетворяющее дополнительным
условиям (3)
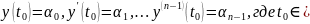 .
Условия (3) называются начальными
условиями ЗК. Легко показать, что ЗК (2)
(3)
.
Условия (3) называются начальными
условиями ЗК. Легко показать, что ЗК (2)
(3)
 Эквивалентна ЗК для СЛОДУ :
Эквивалентна ЗК для СЛОДУ :

В данном
случае
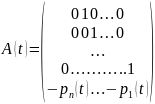 ,
,
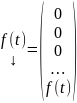 Из связи ЗК (2) (3) с ЗК для СЛОДУ с
непрерывными коэффициентами
Из связи ЗК (2) (3) с ЗК для СЛОДУ с
непрерывными коэффициентами
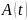 и
получаем:
и
получаем:
Теор. (ТСЕ)
Если
 ,
то для
набора
,
то для
набора
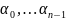 на всем
решение ЗК (1), (2) теорема носит глобальный
характер
на всем
решение ЗК (1), (2) теорема носит глобальный
характер
Вопрос 25
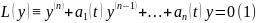
Опр.
Функции
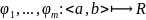 называются ЛЗ на
,
если существуют вещественные числа, не
все равнее нулю, такие, что при всех
называются ЛЗ на
,
если существуют вещественные числа, не
все равнее нулю, такие, что при всех
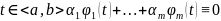 .
В противном случае функции
.
В противном случае функции
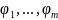 называются ЛНЗ на
называются ЛНЗ на
Утв.
Любые (n+1) решений уравнения
(1) ЛЗ на
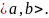
Док-во: Пусть
 решения
уравнения (1) на
Составим их линейную комбинацию и
приравняем ее к нулю
решения
уравнения (1) на
Составим их линейную комбинацию и
приравняем ее к нулю
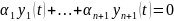 .
Последовательно дифференцируем это
равенство (n-1) раз. В
результате получим следующую систему
n уравнений
.
Последовательно дифференцируем это
равенство (n-1) раз. В
результате получим следующую систему
n уравнений
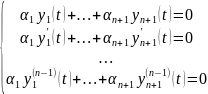 Зафиксируем
в этой системе уравнений.
Зафиксируем
в этой системе уравнений.
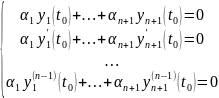 Относительно
переменных
Относительно
переменных
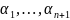 это однородная система линейных
алгебраических уравнений, у которой
число уравнений (n) меньше
числа неизвестных (n+1),
поэтому она имеет бесконечное множество
нетривиальных решений. Пусть
это однородная система линейных
алгебраических уравнений, у которой
число уравнений (n) меньше
числа неизвестных (n+1),
поэтому она имеет бесконечное множество
нетривиальных решений. Пусть
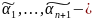 одно
из них. Рассмотрим функцию
одно
из них. Рассмотрим функцию
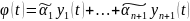 .
Эта функция является решением уравнения
(1). Кроме того,
.
Эта функция является решением уравнения
(1). Кроме того,
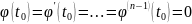 .
Тогда
.
Тогда
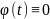 на
,
а это и означает ЛЗ
на
,
а это и означает ЛЗ
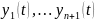 на
на
Утв. У уравнения (1) на существует n ЛНЗ решений.
Док-во:
Пусть
 решений уравнения (1), удовлетворяющих
следующим начальным условиям
решений уравнения (1), удовлетворяющих
следующим начальным условиям
 .
Покажем, что они ЛНЗ.
.
Покажем, что они ЛНЗ.
 Последовательно дифференцируем это
равенство n-1 раз
Последовательно дифференцируем это
равенство n-1 раз
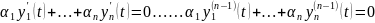 .
Положим
.
С учетом начальных условий (2) получаем
.
Положим
.
С учетом начальных условий (2) получаем
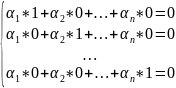 Отсюда
Отсюда