Вопрос 1. Основные определения.

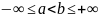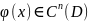Пусть один из промежутков ( , где . Будем говорить, что , если непрерывны на D.

Рассмотрим область . Пусть , причем определена функция

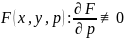в G.

Опр. 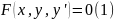, где 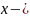независимая переменная, а 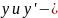неизвестная функция и ее производная соответственно называется ОДУ 1-го порядка, не разрешенным относительно производной.

Опр. Функция называется частный решением ОДУ (1) на D, если

1. 

2. 

Опр. Общим решением ОДУ (1) называется совокупность всех частных решений.

Если (1) удается в некоторой области разрешить относительно 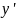, то оно принимает вид : , которое называется ОДУ 1-го порядка, разрешенным относительно производной. Его частное и общее решения определяются аналогично.

Опр. Пусть – частное решение (1) или (2). На плоскости 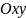оно представляет кривую, которая называется интегральной кривой соответствующих уравнений.

Рассмотрим простейшее ОДУ 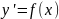. Его общим решением будет 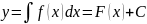. В дальнейшем увидим, что это является общей ситуацией, т.е. общее решение ОДУ 1-го порядка содержит 1 произвольную постоянную. На плоскости общее решение будет представлять собой совокупность интегральных кривых.

Опр. В области существования и единственности решение ЗК общим решением уравнения (2) называется дифференцируемая функция такая, что :

1. Для частное решение ОДУ (2)

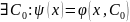
2. Для решение (2)

Опр. Соотношени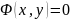е , где 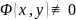на D, называют частным интегралом на D уравнения (2), если 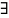решение уравнения (2) такое, что

Замеч. Из частного интеграла по теореме о неявной функции может быть получено частное решение ОДУ (2)

Опр. Общим интегралом уравнения наз. ф-ия , но сохраняющая постоянное значение на любом решении уравнения (2). Иногда общим интегралом называется само соотношение или более общее

Замеч. Из общего интеграла по теореме о неявной функции может быть получено общее решение.

Вопрос 2.

Опр. Задача нахождения интегральной кривой уравнения (2), проходящей через заданную точку 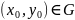называется задачей Коши (ЗК) для уравнения (2). Математически она формулируется так: . Второе условие в системе называется начальным условием ЗК.

В каждой точке уравнение(2) однозначно определяет направление касательной к интегральной кривой, проходящей через эту точку.

Интегральные кривые уравнения (2) не могут пересекаться (могут только касаться).

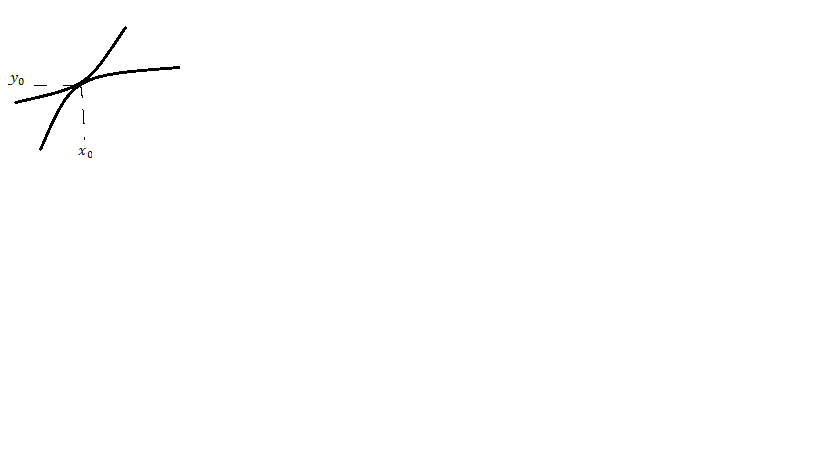В случае касания ЗК в окрестности этой точки имеет не единственное решение.

Теор. (О существовании и единственности решения ЗК для уравнения (2)) (далее ТСЕ)

Пусть . Если и непрерывны в П по совокупности переменных, то 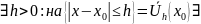решение ЗК (3), причем единственное. ( , где

Замеч.

1. Теорема имеет локальный характер, т.е. гарантирует, что решение существует в некоторой окрестности точки . Однако во всей гарантируется единственность решения понимаемое в следующем смысле. Пусть 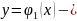решение ЗК(3) на 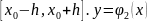– какое-либо решение ЗК(3) н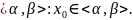а Тогда на

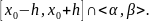
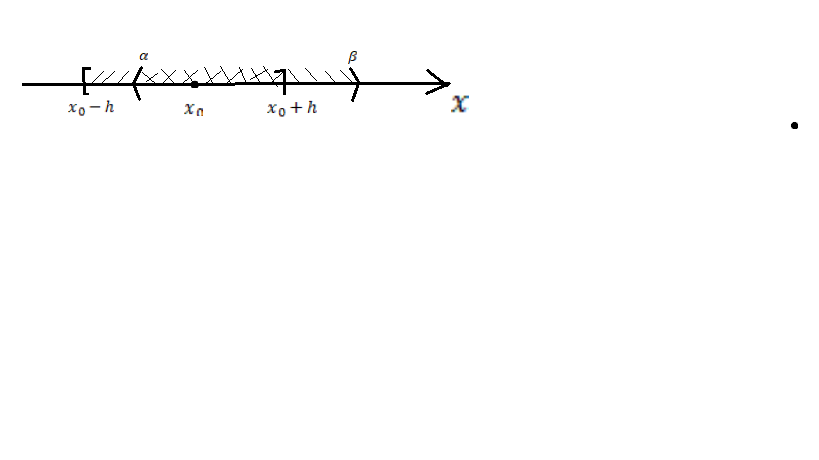
2. Решение ЗК(3) существует при выполнении только лишь условия , но при этом не гарантируется единственность.

3. Условие можно заменить на огр в П или условие Липшица.

4. Эта теорема является достаточным условием

5. Если при движении по отрезку 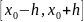в других точках также выполняестя условие ТСЕ, то решение часто удается продлить дальше, иногда на полупрямую и всю прямую.