Решение

Построим графики функций y = f(x₁) и y = f(x₂) и найдем их линейное приближение.

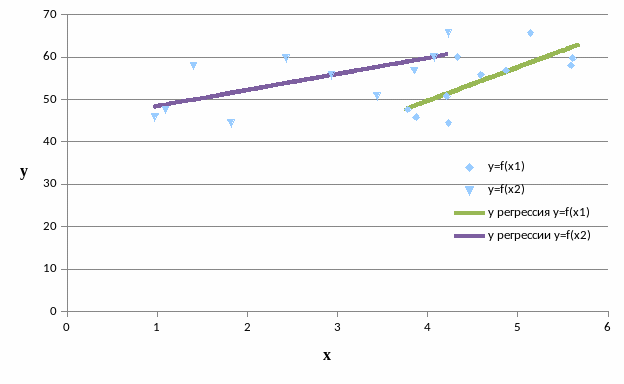
Рисунок 2 – Графики функций y = f(x₁) и y = f(x₂)

При помощи статической формулы посчитаем коэффициент корреляции для каждого графика.

Для зависимости y = f(x₁) К_кор. составил 0,7473, для y = f(x₂) К_кор.= 0,6808. Значения коэффициентов корреляции, посчитанные «вручную» совпали со значениями, посчитанными используя встроенные возможности MS Excel.

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока (табл.6), в которой определенному числовому значению соответствует качественная характеристика.

Значение Ккор.	Характеристика силы связи
0-0,3	корреляционная связь очень слабая
0,3-0,5	слабая
0,5-0,7	средней силы
0,7-0,9	высокая
0,9-1	очень высокая сила корреляции

Таблица 6 – Шкала Челдока

Соотнеся вышеприведенные результаты вычисления коэффициентов корреляции, приходим к выводу, что «теснота связи» в функции y = f(x₁) между независимой переменной x_1­­ и зависимой y высокой силы, а в функции y = f(x₂) – средняя сила связи корреляции между независимой переменной x_2­­ и зависимой y.

Задание №3

В данном задании проверку на «промах» осуществить двумя методами: с помощью правила 2-сигм и критерия максимального отклонения r_max. В случае, если методы дают противоречивые результаты, использовать в качестве ответа тот вывод, который получается по критерию максимального отклонения.

Содержание фосфора в чугуне по данным атомно-эмиссионного анализа составляет, %: 0,17; 0,16; 0,13; 0,15; 0,19; 0,26; 0,2; 0,18; 0,14. Является ли величина 0,26 % промахом?

Решение Метод максимального отклонения

Д ля определения «промаха» методом максимального отклонения воспользуемся формулой

где S(y_k) – оценка среднеквадратичного отклонения единичного результата, рассчитываемая как

|Δy_k|_max – разность – результата опыта¹ – и ;

m – количество проведенных испытаний.

1. Найдем :

k	1	2	3	4	5	6	7	8	9	Σ
yk, %	0,17	0,16	0,13	0,15	0,19	0,26	0,2	0,18	0,14	1,58
Δyk, %	-0,01	-0,02	-0,05	-0,03	0,01	0,08	0,02	0	-0,04	-0,04
Δyk2,%	0,0001	0,0004	0,0025	0,0009	0,0001	0,0064	0,0004	0	0,0016	0,0124

2. Рассчитаем среднеквадратичное отклонение единичного результата:

3. Теперь можем вычислить критерий максимального отклонения:

Сравнивая полученное значение критерия максимального отклонения с табличным значением 2,24>2,18, делаем вывод, что ошибки в опыте №6 допущено не было и значение 0,26 в ряде исследований не следует считать «промахом».