МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

──────────────────────────────────────

Факультет СиСС

Кафедра общей теории связи

ЛАБОРАТОРНАЯ РАБОТА

№ 26-1

по дисциплине «Цифровая обработка сигналов» на тему:

«Анализ нерекурсивных цифровых фильтров 1-го и 2-го порядка»

Вариант №3

Выполнил: студ. гр. БСС2201

Васильев Пётр Алексеевич

Проверил: проф. каф. ОТС

Волчков В. П.

(Осенний семестр)

Москва 2024

1. Цель работы

На персональном компьютере провести анализ нерекурсивных (трансверсальных) цифровых фильтров (ЦФ) 1-го и 2-го порядка; исследовать частотные и временные характеристики фильтров, а также их взаимосвязь со значениями коэффициентов (параметров) ЦФ.

2. Выполнение домашнего задания

2.1. Исходные данные варианта

Табл. 1. Таблица значений исходных данных

Порядок фильтра
1	1	0.64	8 кГц

2.2 Запись разностного уравнения и системной функции

Разностное уравнение нерекурсивного ЦФ -1 (первого порядка) имеет вид:

(1)

где:

- коэффициенты разностного уравнения;

- входной сигнал с задержкой 0,1,2…;

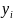- выходной сигнал

Подставим исходные данные из табл. 1 в формулу (1), получим:

(2)

Пусть задан дискретный сигнал Тогда его односторонним Z-преобразованием называется:

(3)

Пусть на входе ЦФ действует сигнал , а на выходе наблюдается сигнал . Тогда системной функцией ЦФ называется отношение:

(4)

Свойство линейности Z – преобразования:

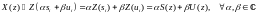(5)

Свойство смещения Z – преобразования:

(6)

Системная функция нерекурсивного ЦФ находится с помощью:

(7)

Получаем преобразованную системную функцию нерекурсивного фильтра:

(8)

Подставим исходные данные в формулу 8 и получим системную функцию нерекурсивного ЦФ 1-го порядка в соответствии с вариантом:

(9)

2.3 Построение структурной схемы ЦФ

Рис. 1. Структурная схема ЦФ 1-го порядка ( = 1; = 0,64)

С труктурная схема ЦФ упрощенно изображает алгоритм работы фильтра. В нерекурсивных (трансверсальных) фильтрах на такой схеме видно, что выходной сигнал фильтра зависит исключительно от входной последовательности.

2.4 Расчет и построение характеристик ЦФ

Импульсная реакция – отклик ЦФ на входной единичный импульс:

(10)

где - единичный импульс Кронекера:

(11)

Используя формулы (1), (11) и начальными условиями получаем импульсную реакцию заданного нерекурсивного ЦФ 1-го порядка:

(12)

График импульсной реакции , построенный с использованием математического пакета Matlab, изображен на рис. 2.

Рис. 2. Импульсная реакция нерекурсивного ЦФ 1-го порядка ( = 1; = 0,64)

Переходная функция – это отклик ЦФ на дискретный единичный скачок:

(13)

Используя формулы (1) и (14) и начальные условия получаем переходную характеристику заданного нерекурсивного ЦФ 1-го порядка:

(14)

График переходной характеристики , построенный с использованием математического пакета Matlab, изображен на рис. 3.

Рис. 3. Переходная характеристика ЦФ 1-го порядка ( = 1; = 0,64)

Комплексным коэффициентом передачи ЦФ называется функция частоты :

(15)

- частота дискретизации, T – период дискретизации [c]

[c] (16)

Амплитудно-частотной характеристикой ЦФ называется функция частоты:

(17)

Где -оператор взятия модуля комплексного числа. По определению модуля комплексного числа :

(18)

По формуле Эйлера:

(19)

(20)

Следовательно, АЧХ ЦФ рассчитывается по следующей формуле:

(21)

Произведя замену в формуле (9) , где - круговая частота [рад/c], и также воспользуюсь формулой (16), при взятии в модуль получаем АЧХ ЦФ:

(22)

График амплитудно-частотной характеристики 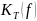, построенный с использованием математического пакета Matlab, изображен на рис. 4.

Рис. 4. АЧХ нерекурсивного ЦФ 1-го порядка ( = 1; = 0,64)

Рассчитаем ФЧХ ЦФ, с помощью аргумента функции :

(23)

График фазо-частотной характеристики ,построенный с использованием математического пакета Matlab, изображен на рис. 5

Риc. 5. ФЧХ ЦФ 1-го порядка ( = 1; = 0,64)

3. Выполнение лабораторной работы

3.1. Исходные данные

Исходные данные представлены в табл. 2. в соответствии с заданием.

Табл. 2. Значения коэффициентов для фильтра

Номер фильтра	Порядок фильтра
1	1	1	0.94	0
2	1	1	-1.06	0
3	2	1	1	-0.06
4	2	1	-1	-0.06
5	2	1	0	0.94
6	2	1	0	-1.06

3.2 Структурная схема нерекурсивного ЦФ 2-го порядка

11\* MERGEFORMAT ()

Структурная схема исследуемого нерекурсивного ЦФ 2-го порядка показана на рис. 6.

3.3. Результаты лабораторного эксперимента

Снятие временных и частотных характеристик нерекурсивных ЦФ было произведено при значениях коэффициентов, взятых из табл.2.

В данном отчете приведены импульсные характеристики (ИХ), амплитудно-частотные характеристики (АЧХ), фазо-частотные характеристики (ФЧХ), которые рассчитываются по данным формулам:

ИХ ЦФ 1-го порядка определяется по формуле (12).

АЧХ ЦФ 1-го порядка определяется по формуле (22).

ФЧХ ЦФ 1-го порядка определяется по формуле (23).

ИХ фильтра второго порядка:

(26)

Найдем системную функцию ЦФ 2-го порядка применим к обоим частям уравнения (25) и воспользовавшись свойствами линейности и смещения, а также формулой (6).

22\* MERGEFORMAT ()

Найдем КЧХ ЦФ 2-го порядка по формулам (12), (16) и (17):

33\* MERGEFORMAT ()

Найдем по формулам (13) и (14):

44\* MERGEFORMAT ()

Найдем АЧХ ЦФ 2-го порядка по формулам (21) и (29):

55\* MERGEFORMAT ()

Найдем ФЧХ ЦФ 2-го порядка по формуле (23):

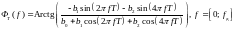66\* MERGEFORMAT ()

3.4. Результаты экспериментального исследования

Рис. ИХ-1 ( )	Рис. ИХ-2 ( )
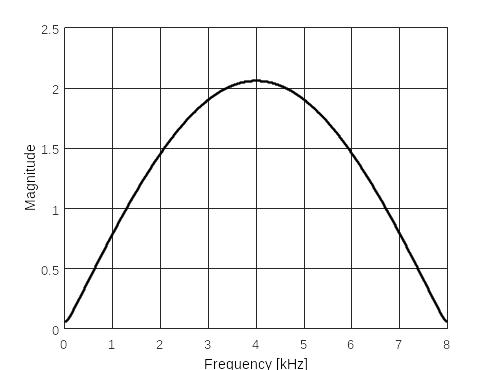
Рис. АЧХ-1 ( )	Рис. АЧХ-2 ( )
Рис. ФЧХ-1 ( )	Рис. ФЧХ-2 ( )
Рис. ИХ-3 ( )	Рис. ИХ-4 ( )
Рис. АЧХ-3 ( )	Рис. АЧХ-4 ( )
Рис. ФЧХ-3 ( )	Рис. ФЧХ-4 ( )
Рис. ИХ-5 ( )	Рис. ИХ-6 ( )
Рис. АЧХ-5 ( )	Рис. АЧХ-6 ( )
Рис. ФЧХ-5 ( )	Рис. ФЧХ-6 ( )

4. Детальные выводы по работе

4.1. Анализ устойчивости

Нерекурсивные фильтры являются устойчивыми, так как при любых начальных условиях реакция фильтра на любое ограниченное воздействие также ограничена (имеет конечную импульсную характеристику), а также потому что линейные цепи не имеют обратной связи.

4.2. Классификация фильтров

Вид фильтра определяется по характеру локализации АЧХ в рабочем диапазоне частот. Следовательно подаваемый сигнал не должен иметь ширину полосы, выходящую за пределы рабочего диапазона, если условие не выполняется, то надо повысить частоту дискретизации, соответственно возрастет и частота Найквиста, что обеспечит выполнение условия.

ЦФ с АЧХ называется ФНЧ, если центральная частота ЦФ принадлежит диапазону .

ЦФ с АЧХ называется ПФ, если центральная частота ЦФ принадлежит диапазону .

ЦФ с АЧХ называется ФВЧ, если центральная частота ЦФ принадлежит диапазону .

ЦФ с АЧХ называется РФ, если его дополняющая АЧХ описывает ПФ.

Фильтры, полученные в результате выполнения лабораторной работы:

Фильтр №1: ФНЧ 1-го порядка ( )

Фильтр №2: ФВЧ 1-го порядка ( )

Фильтр №3: ФНЧ 2-го порядка ( )

Фильтр №4: ФВЧ 2-го порядка ( )

Фильтр №5: РФ 2-го порядка ( )

Фильтр №6: ПФ 2-го порядка ( )

4.3. Анализ поведения АЧХ

Сравнение ФНЧ 1-го порядка (фильтр №1) и ФНЧ 2-го порядка (фильтр №3):

• Ширина пропускания ФНЧ 1-го порядка (1620 Гц) шире полосы пропускания ФНЧ 2-го порядка (1560 Гц);

• Крутизна спада АЧХ ФНЧ 1-го порядка ( ) больше, чем у ФНЧ 2-го порядка ( );

• Пульсации отсутствуют как в полосе пропускания, так и за ее пределами.

Сравнение ФВЧ 1-го порядка (фильтр №2) и ФВЧ 2-го порядка (фильтр №4):

• Ширина пропускания ФВЧ 1-го порядка (1810 Гц) шире полосы пропускания ФВЧ 2-го порядка (1735 Гц);

• Крутизна спада АЧХ ФВЧ 2-го порядка ( ) больше, чем у ФВЧ 1-го порядка ( );

• Пульсации отсутствуют как в полосе пропускания, так и за ее пределами.

4.4. Недостатки и преимущества исследуемых фильтров

Преимущества нерекурсивных фильтров:

• Конечная импульсная характеристика;

• Возможность при соответствующей настройке иметь строго линейную ФЧХ;

• Наглядная связь коэффициентов фильтра с его импульсной характеристикой;

• Абсолютная устойчивость;

• Простота реализации;

Недостатки нерекурсивных фильтров:

• Отсутствует обратная связь;

• Для получения хороших частотных характеристик(например для полосовых фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные фильтры высокого порядка – до нескольких сотен и даже тысяч.
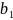