3. Определение характеристик подвески

   1. Расчет характеристики упругого элемента подвески

Подвеска ГМ обязательно включает в себя упругий элемент. В соответствии с техническим заданием упругим элементом является торсион — длинный упругий вал, работающий на кручение. Для расчета характеристик упругого элемента подвески используют следующий алгоритм [1].

Сначала по известным границам допускаемого по показателям самочувствия экипажа диапазона периодов продольно-угловых колебаний определяют предельные жесткости подвески в области статического хода. Далее рассчитывают диаметр торсиона, обеспечивающий максимальное значение динамического хода подвески. Затем вычисляют предельные значения диаметров через предельные жесткости подвески. При нахождении ранее рассчитанного значения в полученном диапазоне его принимают за окончательное. В противном случае выбирают предельное, наиболее близкое к рассчитанному. Как правило, коррекция диаметра торсиона не требуется.

Затем по известному значению диаметра торсиона определяют его допустимый угол закрутки и строят характеристику упругого элемента подвески, приведенную к оси ОК. После рассчитывают величину удельной потенциальной энергии подвески и принимают решение о необходимости установки подрессорника.

Для обеспечения нормального самочувствия экипажа период продольно-угловых колебаний подрессоренного корпуса T_φ должен находиться в диапазоне значений от 0,5 до 1,8 с [1]. При этом для обеспечения более высокой плавности хода и меньшей чувствительности подрессоренного корпуса ГМ к силовому и кинематическому возмущению значение периода следует смещать к правой границе диапазона, особенно при использовании мощных амортизаторов. Связь между жесткостью подвески c и периодом продольно-угловых колебаний подрессоренного корпуса T_φ можно выразить через формулу 1:

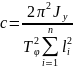, 11\* MERGEFORMAT ()

где J_y — момент инерции подрессоренного корпуса ГМ относительно поперечной оси, проходящей через его центр масс, кг∙м², его можно рассчитать по формуле 2;

T_φ — период продольно-угловых колебаний подрессоренного корпуса ГМ;

l_i — расстояния от центра масс ГМ до i-го ОК.

Момент инерции подрессоренной части корпуса определим по эмпирической формуле (2):

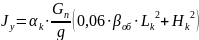, 22\* MERGEFORMAT ()

где α_к — коэффициент влияния масс подрессоренного корпуса ГМ, безразмерная величина, изменяющаяся в диапазоне от 0,5 до 1,0, увеличиваясь с ростом массы ГМ;

G_п — вес подрессоренного корпуса ГМ (обычно равен 0,92…0,94G_ГМ), Н;

g — ускорение свободного падения, м/с²;

β_об — коэффициент распределения масс оборудования, безразмерная величина, изменяющаяся в диапазоне от 1,06 для легкого оборудования, установленного близко к центру масс ГМ, до 1,15 для массивного оборудования, удаленного от центра масс ГМ;

L_к — длина подрессоренного корпуса ГМ, м;

H_к — высота подрессоренного корпуса ГМ, м.

По формуле 2 вычисляют момент инерции подрессоренного корпуса ГМ относительно поперечной оси, проходящей через его центр масс, а по фор- муле 1 — минимальное и максимальное значения жесткостей подвески.

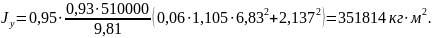
Минимальному значению жесткости подвески c_min соответствует максимальное значение периода продольно-угловых колебаний подрессоренного корпуса ГМ.

а максимальному значению жесткости подвески c_max — минимальное значение периода продольно-угловых колебаний подрессоренного корпуса ГМ

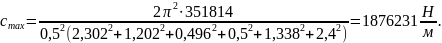
Диаметр торсиона d_т.дин, при котором динамический ход подвески достигает максимума, определяют по формуле 3:

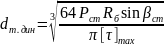, 33\* MERGEFORMAT ()

где P_ст — статическая сила, действующая на ОК, Н;

R_б — радиус балансира, м;

β_ст — статическое угловое положение балансира, град;

[τ]_max — максимально допустимые касательные напряжения в теле торсиона, Па. Для торсионов, подвергаемых заневоливанию, они составляют от 1,1∙10⁹ до 1,6∙10⁹ Па [1]. Для данной машины выбираем максимально возможное значение допускаемых касательных напряжений, так как масса машины является достаточно большой и будет невозможно добиться адекватных характеристик подвески в ином случае.

Статическую силу P_ст, действующую на ОК, определяют по формуле 4:

, 44\* MERGEFORMAT ()

где T₀ — cила предварительного натяжения гусеницы, Н;

— угол наклона ветви гусеницы у направляющего колеса, град;

— угол наклона ветви гусеницы у ведущего колеса, град;

n — число ОК по борту ГМ.

Статическое угловое положение балансира β_ст определяют по формуле 5:

, 55\* MERGEFORMAT ()

где — клиренс ГМ, м;

H — расстояние от днища ГМ до оси крепления балансира в подрессоренном корпусе, м. Ее следует принимать в диапазоне от 0,05 до 0,2 м, в данном случае из конструктивных соображений принимают значение 0,1 м;

h_гус — толщина гусеницы, м;

R_ок — радиус ОК, м;

R_б — радиус балансира, м.

Тогда статическая сила, действующая на один ОК:

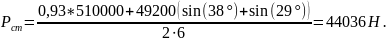
Статическое угловое положение балансира:

Диаметр торсиона, обеспечивающий максимум динамического хода подвески:

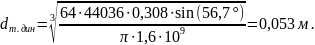
Связь между диаметром торсиона и жесткостью подвески в области статического хода подвески можно выразить через формулу 6:

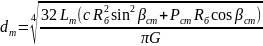, 66\* MERGEFORMAT ()

где L_т — длина рабочего участка торсиона, м;

G — модуль сдвига материала торсиона, Па.

Таким образом, диаметр торсиона, обеспечивающий минимально допустимую жесткость подвески (при длине рабочего участка торсиона L_т = 2,204 м):

Диаметр торсиона, обеспечивающий максимально допустимую жесткость подвески (при длине L_т = 2,204 м):

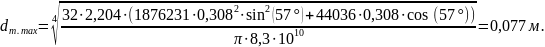
Полученный по формуле 3 диаметр попадает в диапазон допустимых значений.

Далее следует определить максимальный γ_max и статический γ_ст углы закрутки торсиона, а по ним — начальное (нулевое) β₀ и максимальное β_max угловые положения балансира. По ним определяют значения статического f_ст, динамического f_дин и полного f_полн ходов подвески, строят кинематическую схему подвески и получают характеристику упругого элемента подвески, приведенную к ОК.

Максимальный угол закрутки торсиона определяют по формуле 7:

, 77\* MERGEFORMAT ()

.

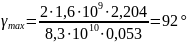Статический угол закрутки торсиона определяют по формуле 8:

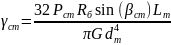, 88\* MERGEFORMAT ()

.

Угловое положение балансира при нулевой закрутке торсиона определяют по формуле 9:

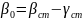, 99\* MERGEFORMAT ()

.

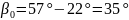Максимальное угловое положение балансира определяют по формуле 10:

, 1010\* MERGEFORMAT ()

.

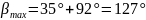Ход подвески (вертикальное перемещение ОК) связан с углом поворота балансира зависимостью 11:

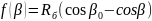. 1111\* MERGEFORMAT ()

Подставляя в формулу 11 значения статического и максимального угловых положений балансира, получают значения статического и полного ходов подвески. Динамический ход подвески рассчитывают как разницу между полным и статическим ходами подвески по формуле 12

. 1212\* MERGEFORMAT ()

Таким образом, по формулам 11 и 12:

.

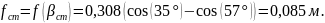
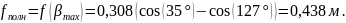
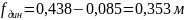Далее динамический ход сравнивают с клиренсом. Для обеспечения удовлетворительной проходимости и уменьшения вероятности удара днищем о неровности при полностью выбранном ходе подвески рекомендуется, чтобы динамический ход был меньше клиренса на 0,100…0,150 м. В данном случае заданная высота клиренса составляет 0,48 м. Запас при полностью выбранном ходе подвески — 0,127 м. Этого достаточно для обеспечения движения ГМ.

Упругий элемент подвески должен обеспечивать достаточную энергоемкость для снижения вероятности «пробоя» подвески во время движения. Удобно оценивать энергоемкость относительной величиной — удельной потенциальной энергией подвески λ, которая отражает отношение запасаемой упругим элементом потенциальной энергии к статической силе, приходящейся на один ОК. Для современных ГМ удельная потенциальная энергия подвески должна быть не менее 0,6..0,8 м[1]. В случае если за счет одного только упругого элемента она не достигает этого значения, и невозможно изменить кинематику подвески, следует ввести в конструкцию подвески подрессорник.

Удельную потенциальную энергию торсионной подвески можно рассчитать по формуле 13, учитывая свойства и физические размеры торсиона:

, 1313\* MERGEFORMAT ()

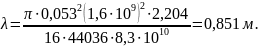
Полученное значение превышает минимально рекомендуемые значения 0,6..0,8 м для удельной потенциальной энергии подвески и является удовлетворительным.

Для построения характеристики упругого элемента подвески, приведенной к оси ОК, необходимо знать, как связаны приведенная к оси ОК сила P и угол поворота балансира β. Эта связь отражена в формуле 14:

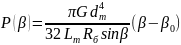. 1414\* MERGEFORMAT ()

На рисунках 1 и 2 представлены кинематическая схема узла подвески, отражающая ее положение при нулевом, статическом и максимальном углах закрутки торсиона, и приведенная к оси ОК характеристика упругого элемента подвески.

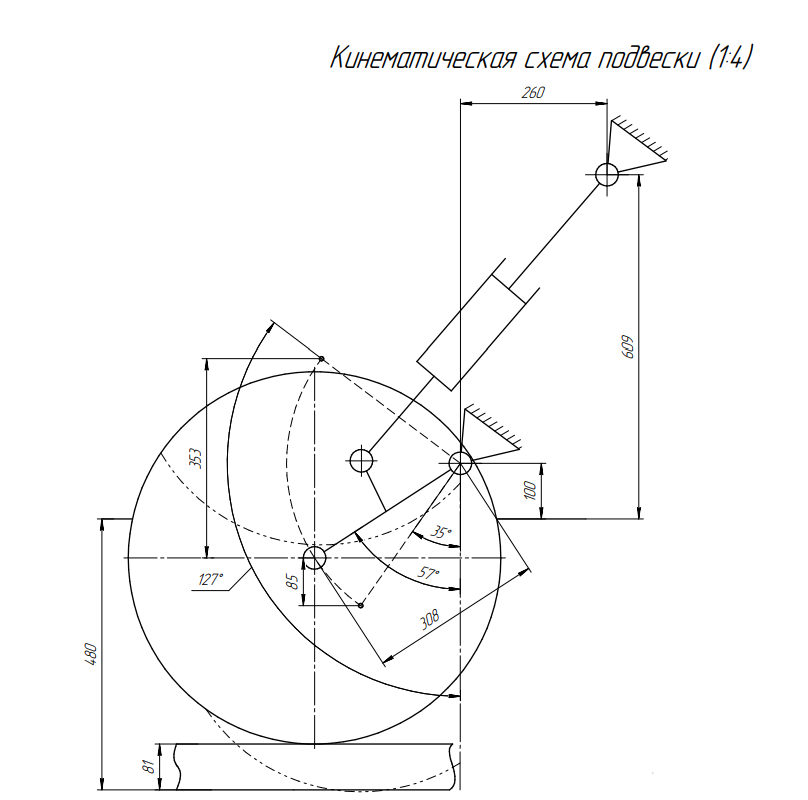
Рисунок 1 — Кинематическая схема подвески в статическом положении

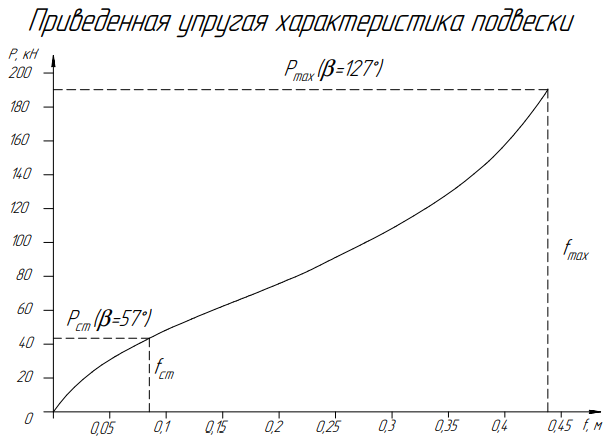
P — приведенная к оси опорного катка сила;

f — вертикальный ход опорного катка;

Рисунок 2 — Упругая характеристика торсионной подвески