5. Расчет на прочность балансира методом конечных элементов

   1. Цель расчета и постановка задачи

Цель расчета: проверить работоспособность балансира по условию прочности в случае пробоя подвески.

Задачи расчета:

1) провести расчет на прочность балансира при нагрузках, возникающих при пробое подвески: силы со стороны подшипниковых узлов катка и отбойника, используя метод конечных элементов с помощью среды ANSYS Workbench;

2) по результатам расчета вычислить коэффициент запаса прочности, сопоставить результаты с допустимыми значениями;

3) сделать вывод о работоспособности балансира из условия прочности.

Объект исследования: балансир.

Допущения:

1) силы, действующие со стороны подшипников заданы векторно;

2) материал балансира сплошной, однородный, изотропный.

3) рассматриваются только упругие деформации, перемещения сечений небольшие.

Эквивалентные напряжения в каждом элементе находятся по теории Мизеса.

2. Создание 3d-модели

3D-модель создана в среде моделирования Siemens NX10, ее визуализация представлена на рисунке 9.

Рисунок 9 — Электронная модель балансира

3. Создание конечно-элементной модели

Конечно-элементная модель создана с использованием конечных элементов TET10, поскольку у детали имеются скошенные грани и преобладают изгибные деформации. Это четырехгранные конечные элементы с десятью узлами, которые расположены в вершинах элемента, а также на серединах его ребер. На рисунке 10 представлена конечно-элементная модель балансира. Принятый размер элемента составляет 3 мм. Общее число элементов составляет 324663, общее число узлов в сетке — 552558.

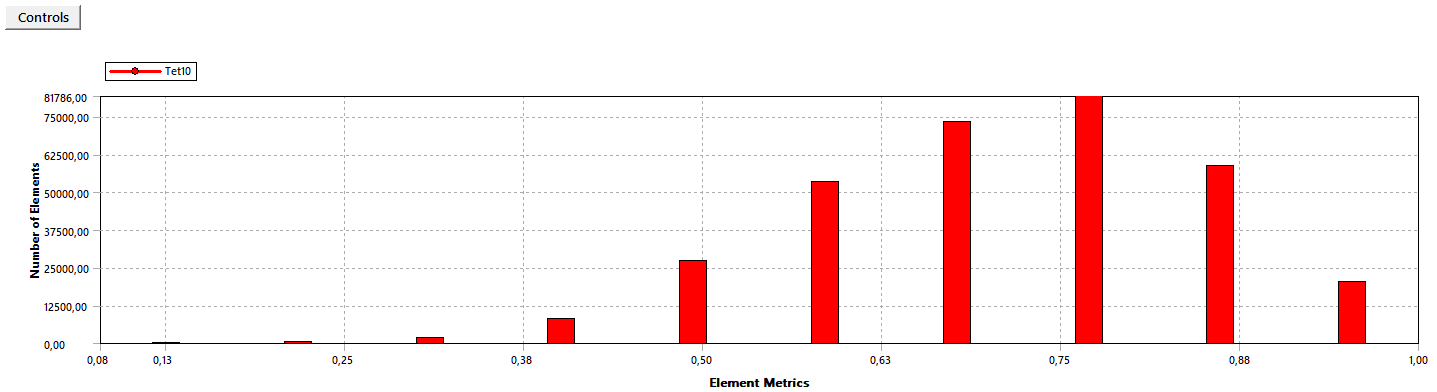
Рисунок 10 — Распределение размеров элементов TET10 в модели

В качестве материала принят материал из библиотеки материалов ANSYS Workbench — Structural Steel. Он обладает схожими характеристиками со сталью 30ХГСА.

Рисунок 11 — Конечно-элементная модель балансира

4. Задание граничных условий и нагрузок

Силы, действующие на балансир представлены в таблице 4 и показаны на рисунке 11.

Таблица 4 — Силовые факторы и ограничения балансира

Зоны	Rx, Н	Rz, Н
Зона C	–14678	14678
Зона B	–29357	29357
Зона A	29914	0
Зона D	Ограничение перемещений вдоль оси Y
Зона F	Ограничение перемещения в осевом направлении
Зона E	Ограничение перемещений вдоль оси Y

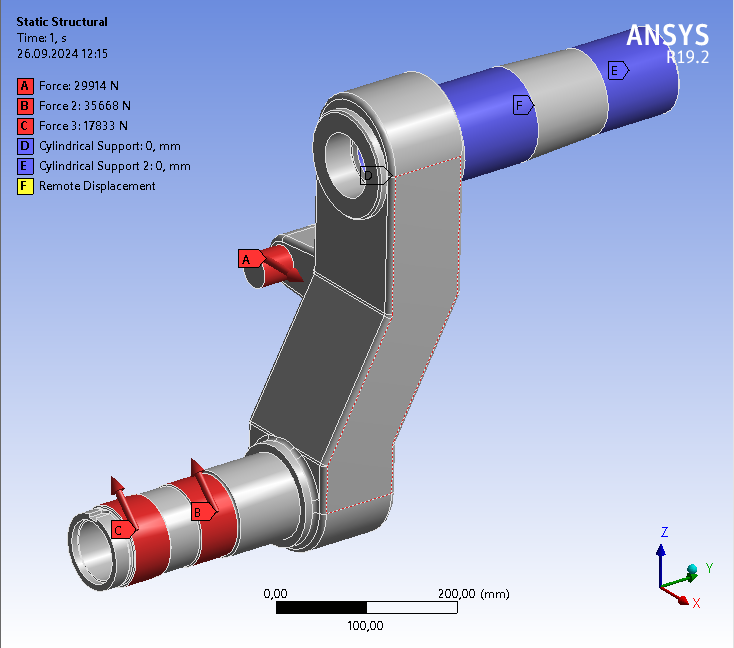
Рисунок 11 — Зоны приложения нагрузок и ограничений

5. Результаты расчета и их анализ

Результатами расчета являются картины напряженного и деформированного состояний. Расчет эквивалентных напряжений производится по закону Мизеса, приведенному в формуле (56).

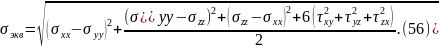
Картина напряженного состояния представлена на рисунках 12-13. Максимальные напряжения составляют 318 МПа.

Рисунок 12 — Напряженное состояние рычага, общая картина, МПа

Рисунок 13 — Область концентрации напряжений

По рисунку 12 видно, что в целом балансир является разгруженным, что говорит о том, что он может быть чрезмерно тяжелый и его можно оптимизировать. Однако для этого необходимо провести ряд дополнительных расчетов при разных режимах движения ГМ.

Основным местом, где концентрируются напряжения является область вокруг шлицевого соединения, воспринимающего момент (рисунок 13).

На рисунке 14 представлено деформированное состояние рычага. Максимальные перемещения узлов составляют 1,39 мм.

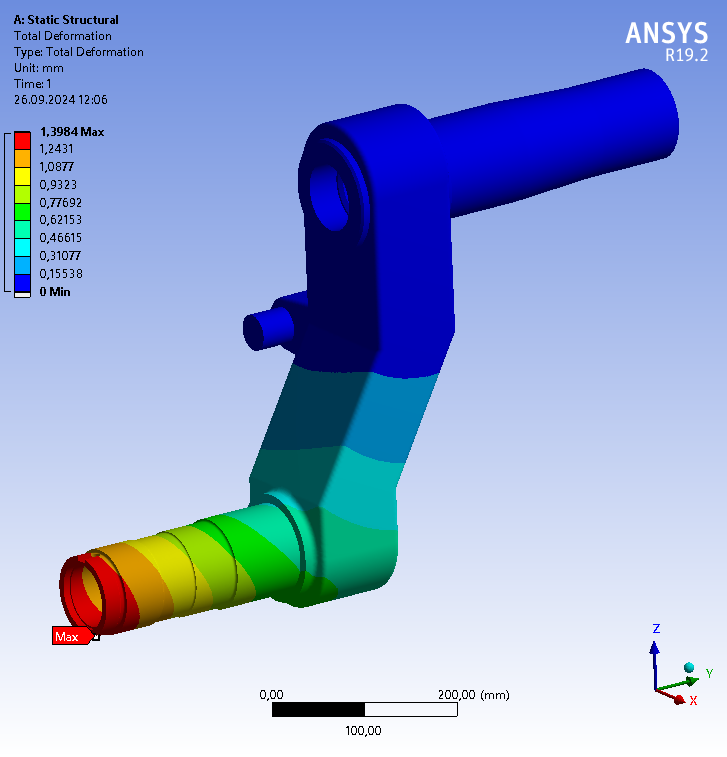
Рисунок 14 – Деформированное состояние балансира, мм

Вычислим коэффициент запаса для стали 30ХГСА, предел текучести которой [σ_т] после обработки составляет 1275 МПа, по формуле 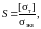(57).

(57)

где σ_экв — максимальные напряжения, МПа.

Таким образом, по формуле 57:

Коэффициент запаса больше минимально допустимого значения, принятого равным 1,3, значит работоспособность балансира обеспечена.