ЦОСл2

Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра безопасности информационных систем (БИС)

СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ ДЛЯ ОБРАБОТКИ ОДНОМЕРНЫХ СИГНАЛОВ

Отчет

по лабораторной работе №2

по дисциплине «Цифровая обработка сигналов»

Студенты гр. 731-2,

«___» _______________ 2024 г

Принял

Преподаватель каф. БИС

«___» _______________ 2024 г

Введение

Цель работы: изучение основ анализа характеристик цифровых фильтров.

Работа была выполнена согласно варианту №2. Значения по варианту представлены на рисунках 1–2.

Рисунок 1 – Вариант работы

Рисунок 2 – Значения по варианту

1 СИНТЕЗ РЕЖЕКТОРНОГО ФИЛЬТРА

Первоочередно необходимо задать центральную частоту, добротность контура и частоту дискретизации, что представлено на рисунке 1.1.

Рисунок 1.1 – Структурная схема цифрового интегратора

1.1 Синтез режекторного фильтра методом инвариантного преобразования импульсной характеристики

При методе инвариантного преобразования. Необходимо правильно выбрать интервал дискретизации Т. Он определяет степень приближения частотных и временных свойств ЦФ к аналоговому фильтру. Чем меньше интервал дискретизации T, тем лучше степень приближения к ИХ аналогового фильтра-прототипа, но при этом увеличивается порядок фильтра.

Операторный коэффициент передачи аналогового режекторного фильтра рассчитывается по формуле 1.1.

		(1.1)
где

Системная функция ЦФ H(z) рассчитывается по формуле 2.1.

		(2.1)
где

1.2 Синтез режекторного фильтра методом отображения дифференциалов

В основе метода лежит дискретизация аналогового фильтра-прототипа, заключающаяся в замене дифференциалов в его дифференциальном уравнении прямыми, обратными или центрированными разностями. Дифференциальное уравнение для аналогового фильтра можно получить непосредственно, либо из операторного коэффициента передачи.

Коэффициенты ЦФ определяются следующими выражениями, представленными на рисунке 1.2

Рисунок 1.2 – Коэффициенты цифрового фильтра методом отображения дифференциалов

При равной частоте дискретизации метод отображения дифференциалов работает хуже, чем метод инвариантного преобразования ИХ. С увеличением частоты дискретизации совпадение характеристик улучшается, но реализация ЦФ становится затруднительной, т.к. требуется повышенное быстродействие ЦФ.

1.3 Синтез режекторного фильтра методом билинейного преобразования

Синтез цифрового фильтра производится по операторному коэффициенту передачи аналогового фильтра-прототипа. Метод несколько сложнее предыдущего, но дает лучшие результаты.

С уменьшением интервала дискретизации T область примерного линейного соответствия цифровых и аналоговых частот увеличивается.

Для решения задачи синтеза ЦФ с заданной частотной характеристикой необходимо так подобрать аналоговый фильтр-прототип, чтобы его частотная характеристика не совпадала точно с ЧХ проектируемого фильтра, а была деформирована по оси частот в соответствии с выражением .

Коэффициенты ЦФ определяются следующими выражениями, представленными на рисунке 1.3

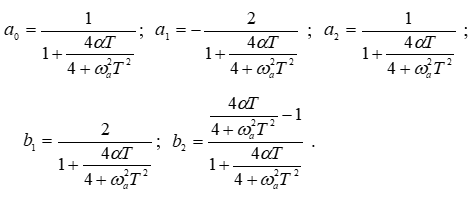
Рисунок 1.3 – Коэффициенты цифрового фильтра методом билинейного преобразования

1.4 Синтез режекторного фильтра методом Z-форм

Алгоритм синтеза ЦФ заключается в следующем:

1. Находим максимальную степень в K(р). Умножаем числитель и знаменатель на p –N.

2. Подставляем выражения для Z-форм.

3. Приводим выражение для системной функции к стандартному виду.

Из формулы операторного коэффициента передачи аналогового режекторного фильтра, представленного в формуле 1.1 получим выражения представленное в формулах 1.2 – 1.3.

	(1.2)
	(1.3)

Коэффициенты ЦФ определяются следующими выражениями, представленными на рисунке 1.4

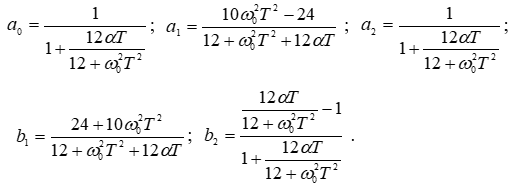
Рисунок 1.4 – Коэффициенты цифрового фильтра методом Z-форм

1.5 Графическое представление методов синтеза

АЧХ и ФЧХ фильтров приведены на рисунках 1.5 – 1.6. Индексы означают соответственно: B – метод билинейного преобразования, I – метод инвариантного преобразования импульсной характеристики, O – метод отображения дифференциалов, Z – метод Z-форм.

Рисунок 1.5 – АЧХ режекторного ЦФ

Рисунок 1.6 – ФЧХ режекторного ЦФ

2 КОРРЕКЦИЯ ЧАСТОТЫ ДЛЯ МЕТОДА БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ

Для метода билинейного преобразования при синтезе режекторного фильтра необходимо произвести коррекцию частоты, при параметрах согласно варианту №2. На рисунках 2.1 – 2.2 показаны АЧХ и AЧХ фильтра, где функции A() и () соответствуют графики с дискретизацией без переопределения частоты настройки, а функции A1() и () – графики с переопределением частоты настройки.

Рисунок 2.1 – АЧХ цифрового фильтра

Рисунок 2.2 – ФЧХ цифрового фильтра

Необходимость коррекции частоты делается для того, чтобы сохранить положение центральной частоты фильтра после билинейного преобразования, требуется предварительная коррекция аналоговой частоты, которая обеспечит соответствие между аналоговых и цифровых шкал

Физический смысл заключается в том, что билинейное преобразование искажает частотную шкалу, и коррекция позволяет восстановить согласованность между частотами, а также для режекторного фильтра важно, чтобы центральная частота подавления​ соответствовала заданной цифровой частоте. Без коррекции фильтр будет настроен на неправильную частоту, что нарушит его функциональность.

3 СИНТЕЗ ФИЛЬТРА БАТТЕРВОРГА 4 ПОРЯДКА

По варианту необходимо задать порядок N=4 аналогового фильтра-прототипа и получить его ЧХ, а затем дискретизируя фильтр методом билинейного преобразования, сравниваем АЧХ и ФЧХ синтезированного ЦФ и аналогового фильтра-прототипа, что представлено на рисунках 3.1 – 3.2.

Рисунок 3.1 – АЧХ фильтра 4-го порядка

Рисунок 3.2 – ФЧХ фильтра 4-го порядка

4 ПЕРЕХОД ОТ ПЕРЕМЕННОЙ ЛАПЛАСА К ПЕРЕМЕННОЙ Z

Переход в символьной области от переменной Лапласа к переменной Z представлен на рисунках 4.1 – 4.2.

Рисунок 4.1 – Процесс вычисления

Рисунок 4.2 – Полученные коэффициенты

Структура фильтра Баттерворта 4го порядка представлена на рисунке 4.3.

Рисунок 4.3 – Структура фильтра Баттерворта 4го порядка

5 ЧАСТОТНЫЕ ПРЕОБРАЗОВАНИЯ ФИЛЬТРА БАТТЕРВОРГА

Полученные АЧХ с вычисленными коэффициентами исходного и преобразованного фильтров, представлены на рисунках 5.1 – 5.4.

Рисунок 5.1 – Преобразование ФНЧ в новый вид ФНЧ

Рисунок 5.2 – Преобразование ФНЧ в ФВЧ

Рисунок 5.3 – Преобразование ФНЧ в ПФ

Рисунок 5.4 – Преобразование ФНЧ в Режекторный фильтр

6 АНАЛИЗ ВЛИЯНИЯ ОШИБОК

Далее был проведен анализ влияния ошибок задания коэффициентов цифрового ФНЧ на АЧХ, с помощью изменения коэффициента b. Результаты представлены на рисунках 6.1 – 6.2.

Рисунок 6.1 – АЧХ идеального ЦФ

Рисунок 6.2 – Функции ошибок

7 КВАНТОВАНИЕ КОЭФФИЦИЕНТОВ

Далее необходимо проквантовать коэффициенты цифрового фильтра с числом двоичных разрядов равным 1, 2, 4, 6, что представлено на рисунках 7.1 – 7.4 соответственно.

Рисунок 7.1 – Число разрядов = 1

Рисунок 7.2 – Число разрядов = 2

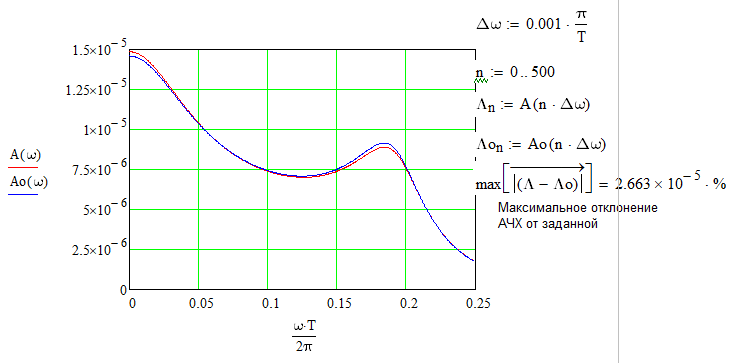
Рисунок 7.3 – Число разрядов = 4

Рисунок 7.4 – Число разрядов = 6

Заключение

В ходе выполнения лабораторной работы были изучены основы анализа характеристик цифровых фильтров.

Томск 2024