9.2 Исследование поля ошибок округления в цифровом фильтре второго порядка c учетом остатков
Поле ошибок округления в цифровом фильтре второго порядка с учетом остатков, представлено на рисунке 9.8. Далее необходимо изучить функциональные зависимости от значений коэффициентов b1 и b2, что представлено на рисунках 9.9 – 9.14.
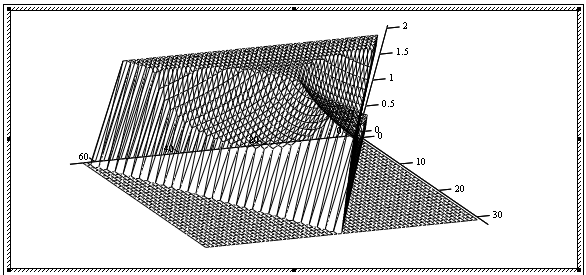
Рисунок 9.8 – Поле ошибок округления в цифровом фильтре второго порядка с учетом остатков
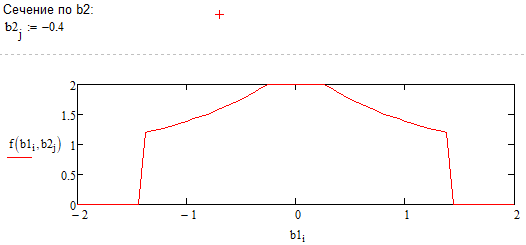
Рисунок 9.9 – Сечение при 𝑏2𝑗 = -0.4 с сохранением остатков
Рисунок 9.10 – Сечение при 𝑏2𝑗 = 0.4 с сохранением остатков
Рисунок 9.11 – Сечение при 𝑏2𝑗 = 0.9 с сохранением остатков
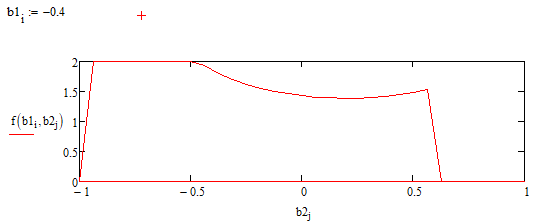
Рисунок 9.12 – Сечение при 𝑏1𝑗 = -0.4 с сохранением остатков
Рисунок 9.13 – Сечение при 𝑏1𝑗 = 0.2 с сохранением остатков
Рисунок 9.14 – Сечение при 𝑏1𝑗 = 0.8 с сохранением остатков
При увеличении коэффициента 𝑏2𝑗 происходит симметричное сужение сечений по b2 относительно 0, а при увеличении b1𝑖 сечение b1 сужается к 0 и в правой части имеет более крутую вогнутость
9.3 Исследование поля относительной дисперсии ошибок для двух вариантов построения цф второго порядка
Поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка, представлено на рисунке 9.15. Далее необходимо изучить функциональные зависимости от значений коэффициентов b1 и b2, что представлено на рисунках 9.16 – 9.21.
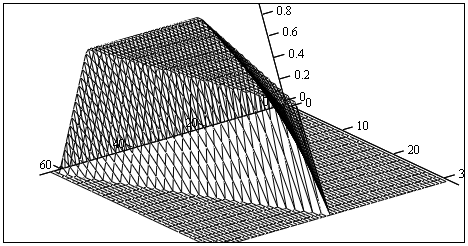
Рисунок 9.15 – Поле относительной дисперсии ошибок для двух вариантов построения ЦФ второго порядка без учета остатков
Рисунок 9.16 – Сечение при 𝑏2𝑗 = -0.4 поля относительной дисперсии
Рисунок 9.17 – Сечение при 𝑏2𝑗 = 0.4 поля относительной дисперсии
Рисунок 9.18 – Сечение при 𝑏2𝑗 = 0.9 поля относительной дисперсии
Рисунок 9.19 – Сечение при 𝑏1𝑗 = -0.4 поля относительной дисперсии
Рисунок 9.20 – Сечение при 𝑏1𝑗 = 0.2 поля относительной дисперсии
Рисунок 9.21 – Сечение при 𝑏1𝑗 = 0.8 поля относительной дисперсии
При увеличении коэффициента 𝑏2𝑗 происходит симметричное сужение к 0, а при увеличении 𝑏1𝑖 правая часть поля становится более крутой и площадь фигуры уменьшается.
Таким образом, можно заметить, что выигрыш происходит на наклонных участках |b1| > 0,5. В этих областях предпочтительнее фильтр с использованием остатков, а на плоских областях лучше использовать фильтр без учета остатков.
Заключение
В ходе выполнения лабораторной работы были изучены основы анализа характеристик цифровых фильтров для обработки одномерных сигналов
Томск 2024