5 Исследование сглаживающего звена

На основе передаточной функции, представленной в формуле 5.1, были найдены коэффициенты цифрового фильтра, а именно a₀=1, b₁=K=0,9 остальные 0. Структурная схема сглаживающего звена представлена на рисунке 5.1. По полученным коэффициентам была сформирована импульсная и переходная характеристики при нулевых начальных условиях, что представлено на рисунках 5.3 – 5.4, а также вычислены АЧХ и ФЧХ, что представлено на рисунках 5.2 и 5.5 соответственно.

(5.1)

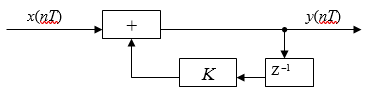
Рисунок 5.1 – Структурная схема сглаживающего звена

При подачи импульсной характеристики на сглаживающее звено на выходе будет происходить экспоненциальное убывание с каждым шагом. Первое значение K=0.9, а затем каждое следующее уменьшается на множитель (1−K)=0.1.

Переходная характеристика описывает реакцию фильтра при нулевых значениях на единичную ступенчатую функцию, для фильтра при K=0.9, переходная характеристика в начальный момент расти от нуля, и постепенно отклик стабилизируется на уровне.

Рисунок 5.2 – Амплитудно-частотная характеристика сглаживающего звена

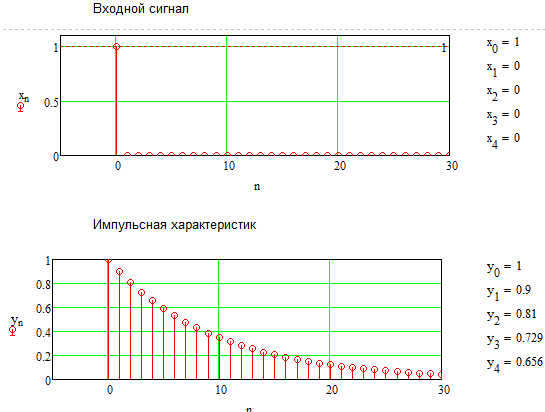
Рисунок 5.3 – Импульсная характеристика входного сигнала

Рисунок 5.4 – Переходная характеристика входного сигнала

Рисунок 5.5 – Фазо-частотная характеристика цифрового сглаживающего звена

6 Исследование фильтра чебышева

На основе варианта, представленного на рисунке, были получены коэффициенты цифрового фильтра, а именно a₀=0.03493, a₁=0.13974, a₂=0.20961, a₃=0.13974, a₄=0.03493, b₁=2.55456, b₂=-3.03822, b₃=1.85615, b₄=-0.49433. Структурная схема фильтра Чебышева представлена на рисунке 6.1. По полученным коэффициентам была сформирована импульсная и переходная характеристики при нулевых начальных условиях, что представлено на рисунках 6.2 – 6.3, а также вычислены АЧХ и ФЧХ, что представлено на рисунках 6.4 – 6.5 соответственно.

Рисунок 6.1 – Структурная схема фильтра Чебышева

Рисунок 6.2 – Амплитудно-частотная характеристика сглаживающего звена

Рисунок 6.3 – Импульсная характеристика входного сигнала

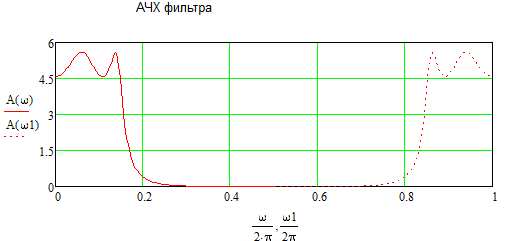
Рисунок 6.4 – Переходная характеристика входного сигнала

Рисунок 6.5 – Фазо-частотная характеристика фильтра Чебышева

Нормированный фильтр нижних частот Чебышева n-го порядка обладает следующими основными свойствами: для ||  1 значения функции |H(j)|2 колеблются между двумя пределами и 1. В общей сложности на интервале 0    1 имеется n критических точек, в которых функция |H(j)|² достигает максимального значения, равного 1, или минимального значения, равного .

При   1 функция |H(j)|² монотонно убывает и стремится к нулю.

Функция |H(j)|2 удовлетворяет следующим условиям:

|H(j₁)|² = , и

|H(j₀)|² = 1, если n нечетно, или

|H(j₀)|² = , если n четно.

Функция фильтра Чебышева имеет только полюсы – числитель ее представляет собой постоянную величину. Полюсы фильтра Чебышева располагаются на эллипсе. Большая ось этого эллипса проходит по мнимой оси p - плоскости, тогда как малая ось – вдоль вещественной оси.

Параметр   определяет неравномерность АЧХ фильтра Чебышева в полосе пропускания

Главным отличием фильтров Чебышева является то, что они обладают свойством оптимальности. Другими словами, если какой-либо фильтр n-го порядка, содержащий только полюсы, имеет в полосе пропускания лучшие характеристики по сравнению с фильтром Чебышева порядка n, то в полосе непропускания характеристики этого фильтра наверняка будут хуже.

Передаточная функция фильтра Чебышева представлена на рисунке 6.6

Рисунок 6.6 – Передаточная функция фильтра Чебышева

Теперь необходимо изменить коэффициенты, чтобы посмотреть на изменения импульсной характеристики, что представлено на рисунках 6.7 – 6.10.

Рисунок 6.7 – Импульсная характеристика при уменьшении а1

Рисунок 6.8 – Импульсная характеристика при увеличенном а1

Рисунок 6.9 – Импульсная характеристика при уменьшении b1

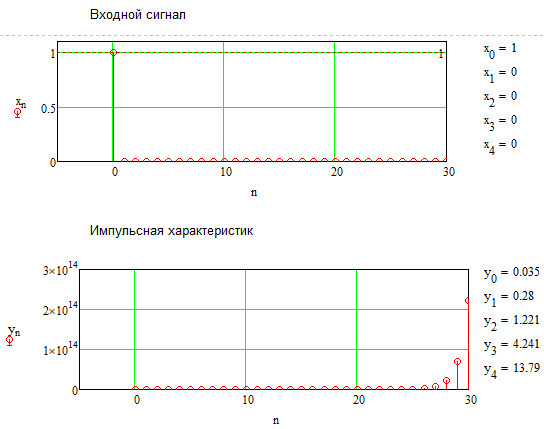
Рисунок 6.10 – Импульсная характеристика при увеличенном b1

Теперь необходимо изменить коэффициенты, чтобы посмотреть на изменения переходной характеристики, что представлено на рисунках 6.11 – 6.14.

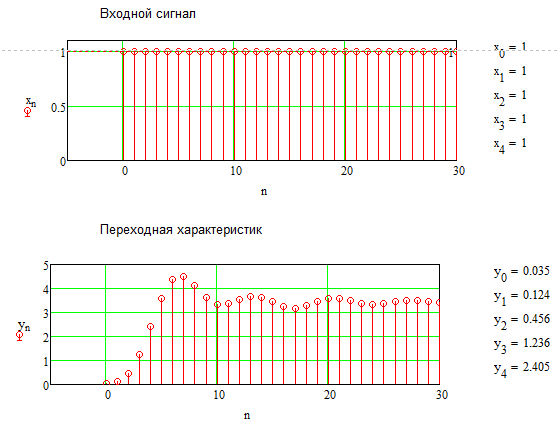
Рисунок 6.11 – Переходная характеристика при уменьшении a1

Рисунок 6.12 – Переходная характеристика при увеличенном a1

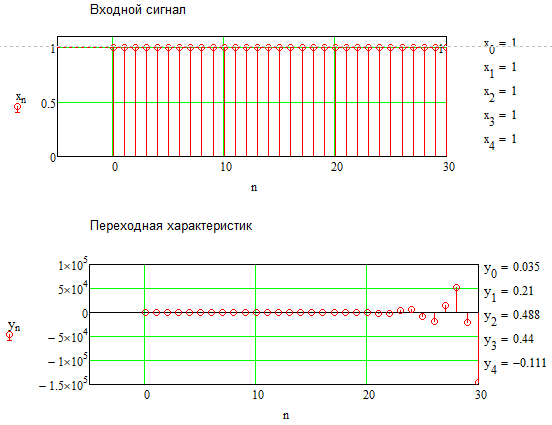
Рисунок 6.13 – Переходная характеристика при уменьшении b1

Рисунок 6.14 – Переходная характеристика при увеличенном b1

Теперь необходимо изменить коэффициенты, чтобы посмотреть на изменения АЧХ, что представлено на рисунках 6.15 – 6.18.

Рисунок 6.15 – АЧХ при уменьшении a1

Рисунок 6.16 – АЧХ при увеличенном a1

Рисунок 6.17 – АЧХ при уменьшении b1

Рисунок 6.18 – АЧХ при увеличенном b1

Теперь необходимо изменить коэффициенты, чтобы посмотреть на изменения ФЧХ, что представлено на рисунках 5.19 – 5.22.

Рисунок 6.19 – ФЧХ при уменьшении a1

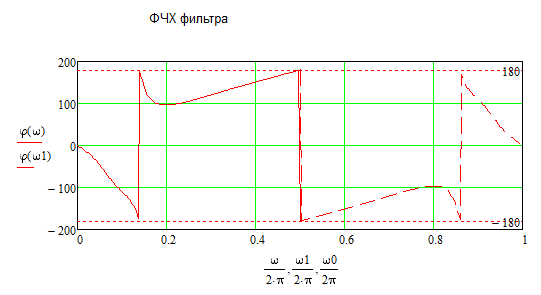
Рисунок 6.20 – ФЧХ при увеличенном a1

Рисунок 6.21 – ФЧХ при уменьшении b1

Рисунок 6.22 – ФЧХ при увеличенном b1