Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра безопасности информационных систем (БИС)

Отчет

по практической работе №1

по дисциплине «Цифровая обработка сигналов»

Студенты гр. 731-2,

«___» _______________ 2024 г

Принял

Преподаватель каф. БИС

«___» _______________ 2024 г

Введение

Цель работы: изучение основ анализа характеристик цифровых фильтров.

Работа была выполнена согласно варианту №2. Значения по варианту представлены на рисунках 1–2, а также в таблице 1.

Рисунок 1 – Вариант работы

Рисунок 2 – Значения по варианту

Таблица 1.1 – Передаточные функции

Цифровой интегратор с ограниченным временем суммирования (М = 8)
Цифровой дифференциатор (В1Р)
Вычислитель 2-й разности (В2Р)
Всепропускающее звено (K = 0,9)
Сглаживающее звено (K = 0,9)

1 Исследование цифрового интегратора с ограниченным временем суммирования

На основе передаточной функции, представленной в формуле 1.1, были найдены коэффициенты цифрового фильтра, а именно a₀=1, a₈=-1, b₀=1, b₁ = -1 остальные 0. Структурная схема цифрового интегратора представлена на рисунке 1.1. По полученным коэффициентам была сформирована импульсная и переходная характеристики при нулевых начальных условиях, что представлено на рисунках 1.2 – 1.3, а также вычислены АЧХ и ФЧХ, что представлено на рисунках 1.4 – 1.5 соответственно.

(1.1)

Рисунок 1.1 – Структурная схема цифрового интегратора

При подачи импульсной характеристики на цифровой интегратор с ограниченным временем суммирования на выходе будет происходить суммирование, которое ограничено количеством отсчетов, которое ограничено 8, после 8 отсчета результаты сводятся к нулю.

Переходная характеристика описывает реакцию фильтра при нулевых значениях на единичную ступенчатую функцию, для фильтра идет увеличение на единицу до 8 отсчета, где достигает ее максимума и после не изменяется.

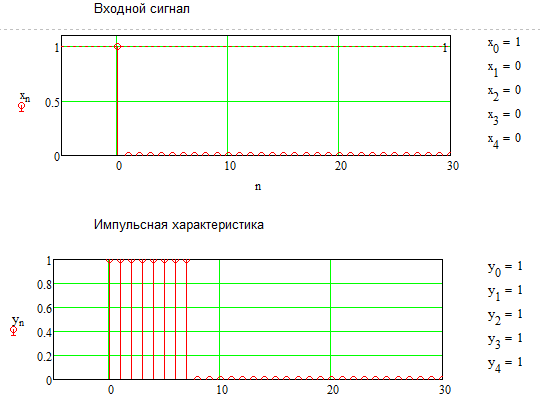
Рисунок 1.2 – Импульсная характеристика входного сигнала

Рисунок 1.3 – Переходная характеристика входного сигнала

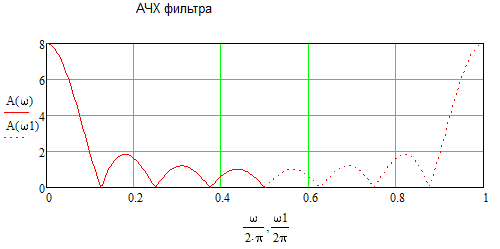
Рисунок 1.3 – Амплитудно-частотная характеристика цифрового интегратора

Рисунок 1.4 – Фазо-частотная характеристика цифрового интегратора

2 Исследование цифрового дифференциатора (в1р)

На основе передаточной функции, представленной в формуле 2.1, были найдены коэффициенты цифрового фильтра, а именно a₀=1, a₁=-1 остальные 0. Структурная схема цифрового дифференциатора представлена на рисунке 2.1. По полученным коэффициентам была сформирована импульсная и переходная характеристики при нулевых начальных условиях, что представлено на рисунках 2.2 – 2.3, а также вычислены АЧХ и ФЧХ, что представлено на рисунках 2.4 – 2.5 соответственно.

(2.1)

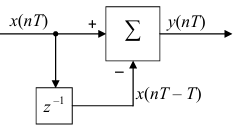
Рисунок 2.1 – Структурная схема цифрового дифференциатора В1Р

При подачи импульсной характеристики на цифровой дифференциатор на выходе будет происходить разность между текущим и предыдущим значениями входного сигнала. Описание по моментам времени представлено в таблице 2.1.

Таблица 2.1 – Состояния цифрового дифференциатора В1Р

Момент времени	Вход	Задержка	Выход
1	1	-	1
2	0	-1	-1
3	0	0	0
4	0	0	0

Переходная характеристика описывает реакцию фильтра при нулевых значениях на единичную ступенчатую функцию, для фильтра идет увеличение на единицу до 1 отсчета, где достигается ее максимум и после обращается в постоянный ноль.

Рисунок 2.2 – Импульсная характеристика входного сигнала

Рисунок 2.3 – Переходная характеристика входного сигнала

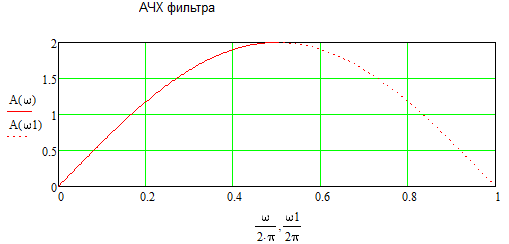
Рисунок 2.4 – Амплитудно-частотная характеристика цифрового дифференциатора В1Р

Рисунок 2.5 – Фазо-частотная характеристика цифрового дифференциатора В1Р