Лабы / lab3ageev

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государтвенный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №3

по дисциплине «Теоретические основы электроники»

Тема: ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Студент гр. 2193		Агеев А.А.
Преподаватель		Кондаков А.В.

Санкт-Петербург

2024

Цели работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Основные теоретические положения.

Свободный процесс – процесс в динамической цепи после коммутации без источников.

В динамических цепях различных порядков свободные процессы (свободные составляющие) описываются однородными линейными дифференциальными

уравнениями; вид свободного процесса определяется корнями характеристического уравнения р_k. (собственными частотами цепи).

Порядок цепи определяется количеством накопителей.

При возбуждении цепи короткими импульсами источника тока реактивные элементы заряжаются, после отключения источника запасенная энергия расходуется резистивными элементами.

Собственные частоты можно рассчитать как нули входной проводимости цепи

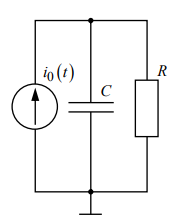
Цепь первого порядка – рисунок 1.

Для цепи первого порядка (рис.1)

Его корень

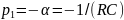
В цепи первого порядка одна собственная частота, вещественная и отрицательная, свободный процесс имеет вид

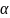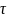где - постоянная затухания, – постоянная времени экспоненты.

Процесс экспоненциальный.

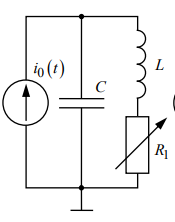
Цепь второго порядка – рисунок 2.

В цепи второго порядка (рис.2)

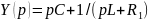
Корни (собственные частоты):

Корни могут быть:

• вещественными различными (апериодический режим):

• кратными вещественными (критический режим): ;

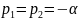• комплексно-сопряженными (колебательный режим):

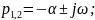
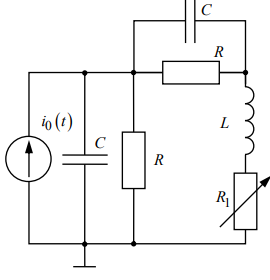
Цепь третьего порядка – рисунок 3.

В цепи третьего порядка (рис.3)

Корни (собственные частоты):

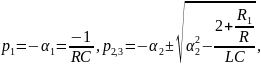
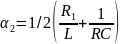
Собственные частоты могут быть:

• три вещественные;

• одна вещественная и две комплексно-сопряженные.

Обработка результатов.

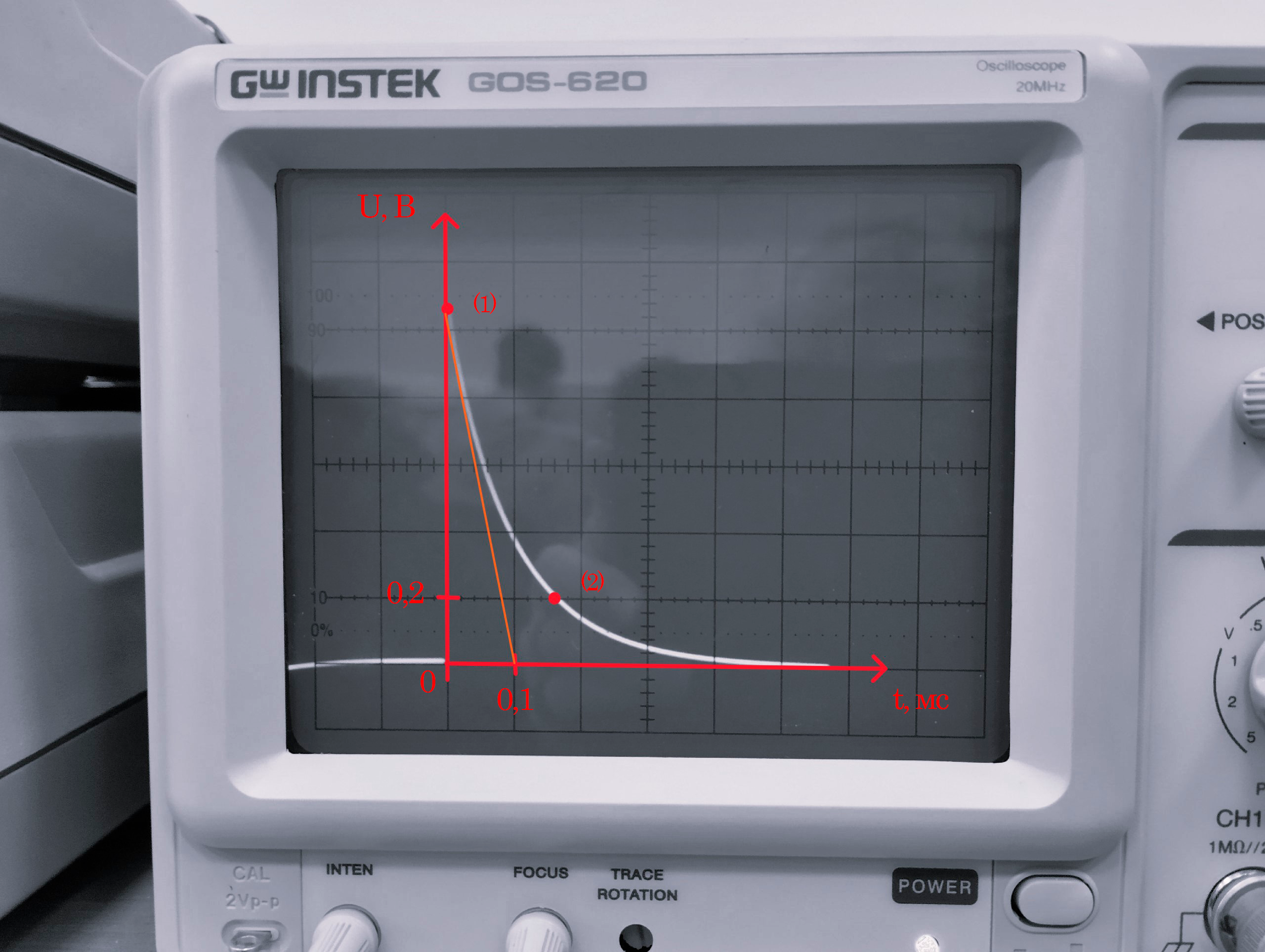
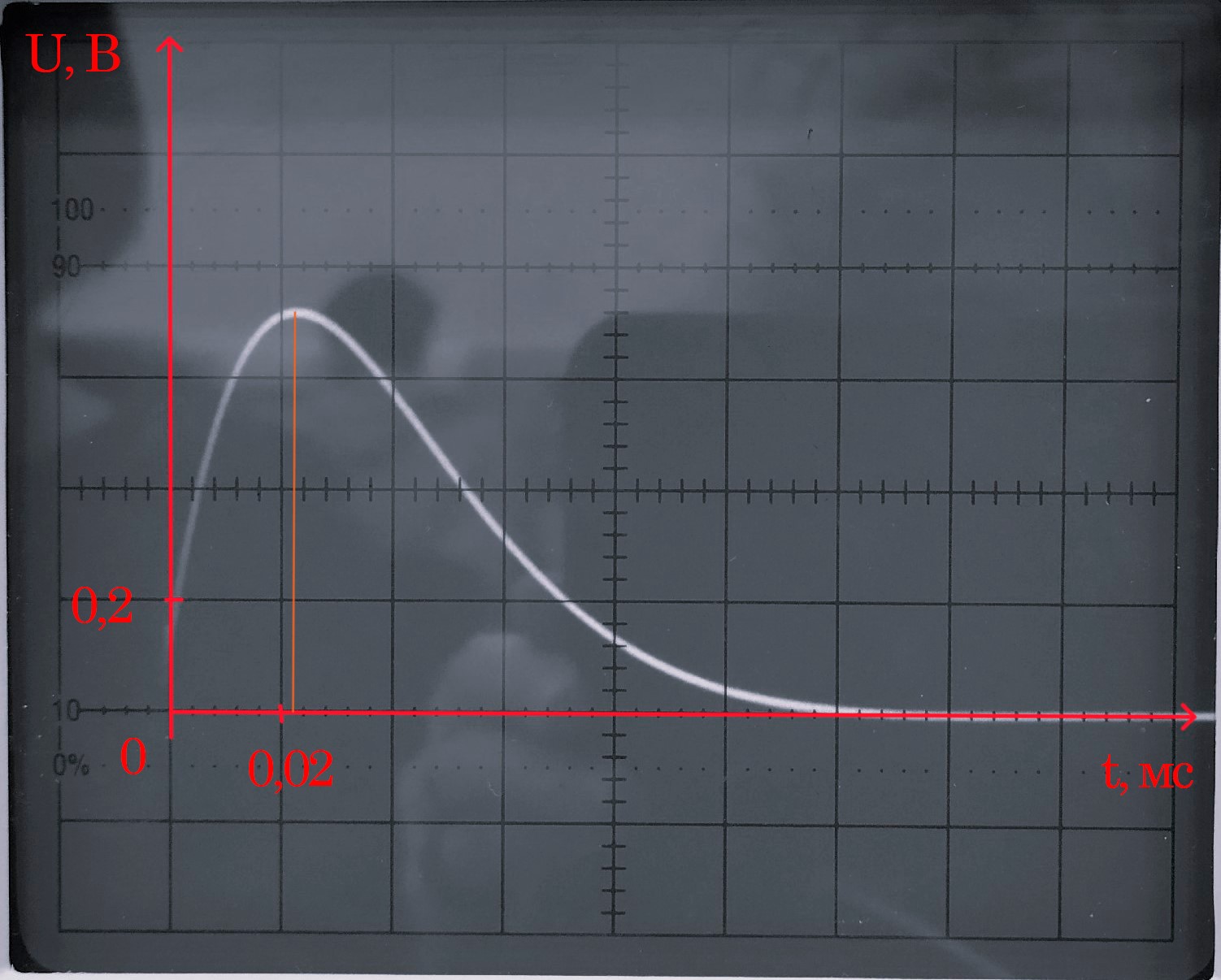
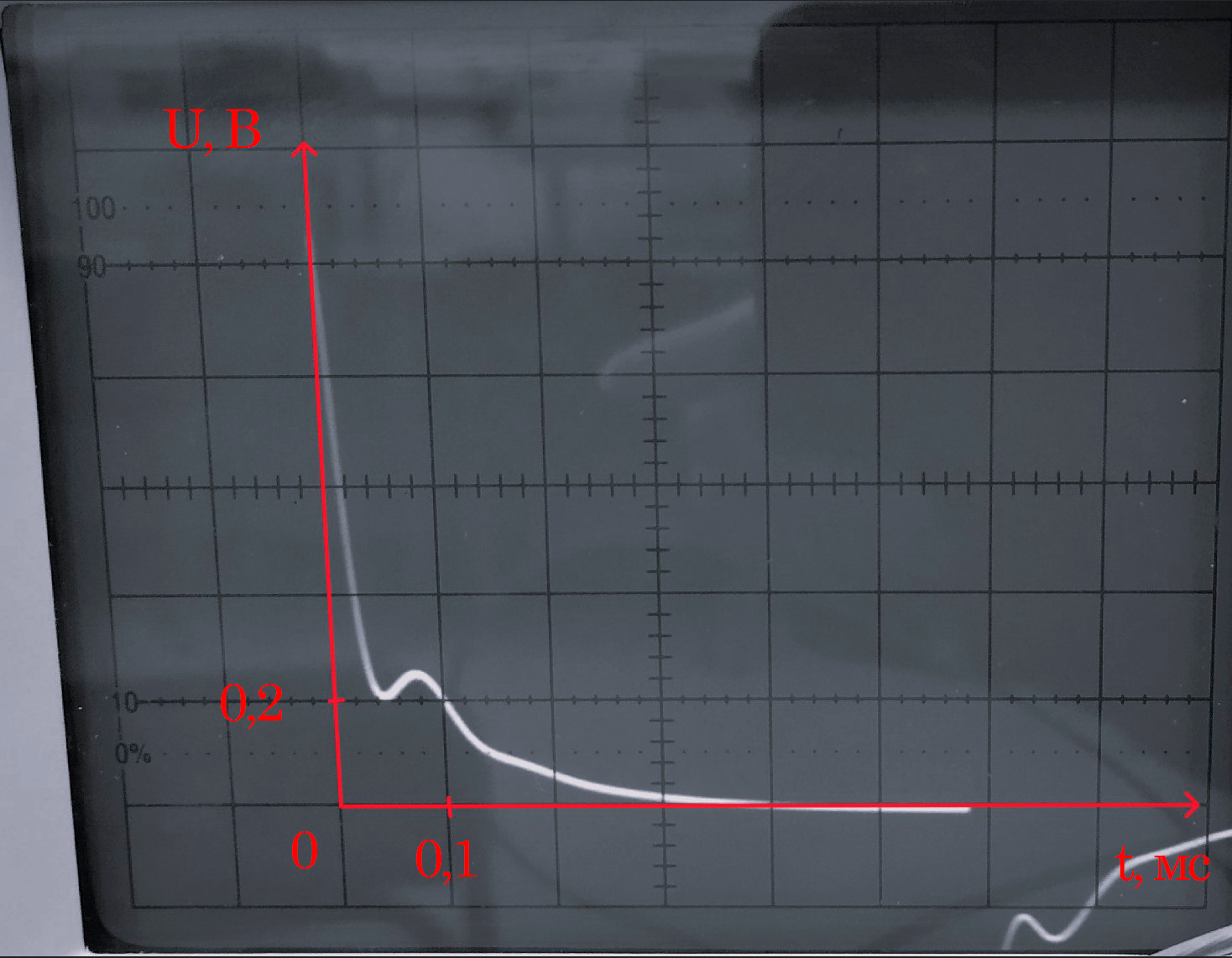
Осциллограмма 1

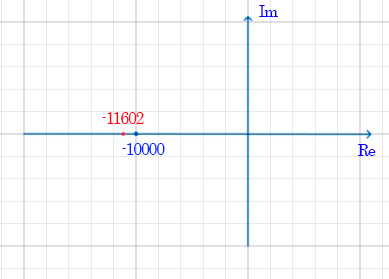
Корень (собственная частота) на комплексной плоскости – рисунок 4

1. Исследование свободных процессов в цепи первого порядка.

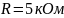
Постоянная времени экспоненты теоретически:

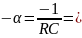
p₁ = 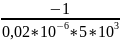= -10 000 с^-1 = -10⁴ с^-1

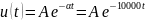
Постоянная времени по осциллограмме 1:

1. ;

;

;

;

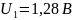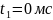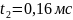α = =

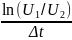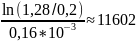
2. По осциллограмме 1 можно провести

подкасательную к любой точке (1) или (2),

которая даст нам значение :

2. Исследование свободных процессов в цепи второго порядка.

Осциллограмма 2

Корень (собственная частота) на комплексной плоскости – рисунок 5

а) Колебательный режим:

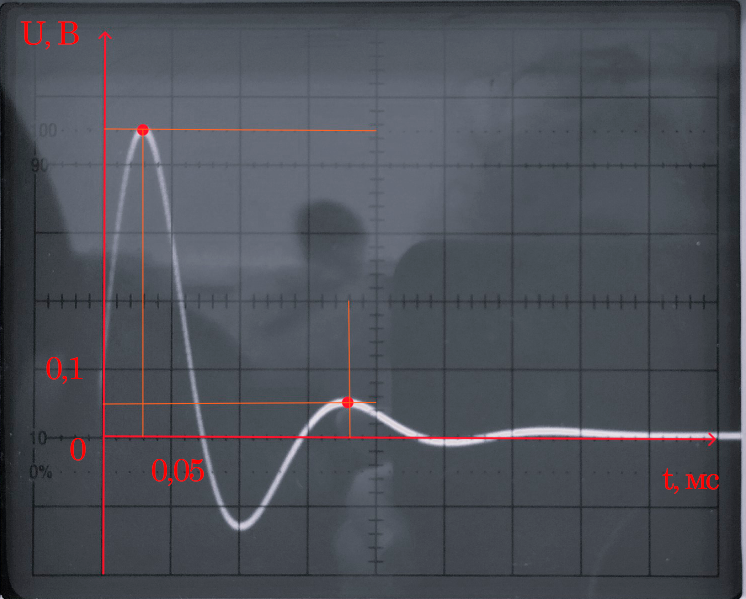
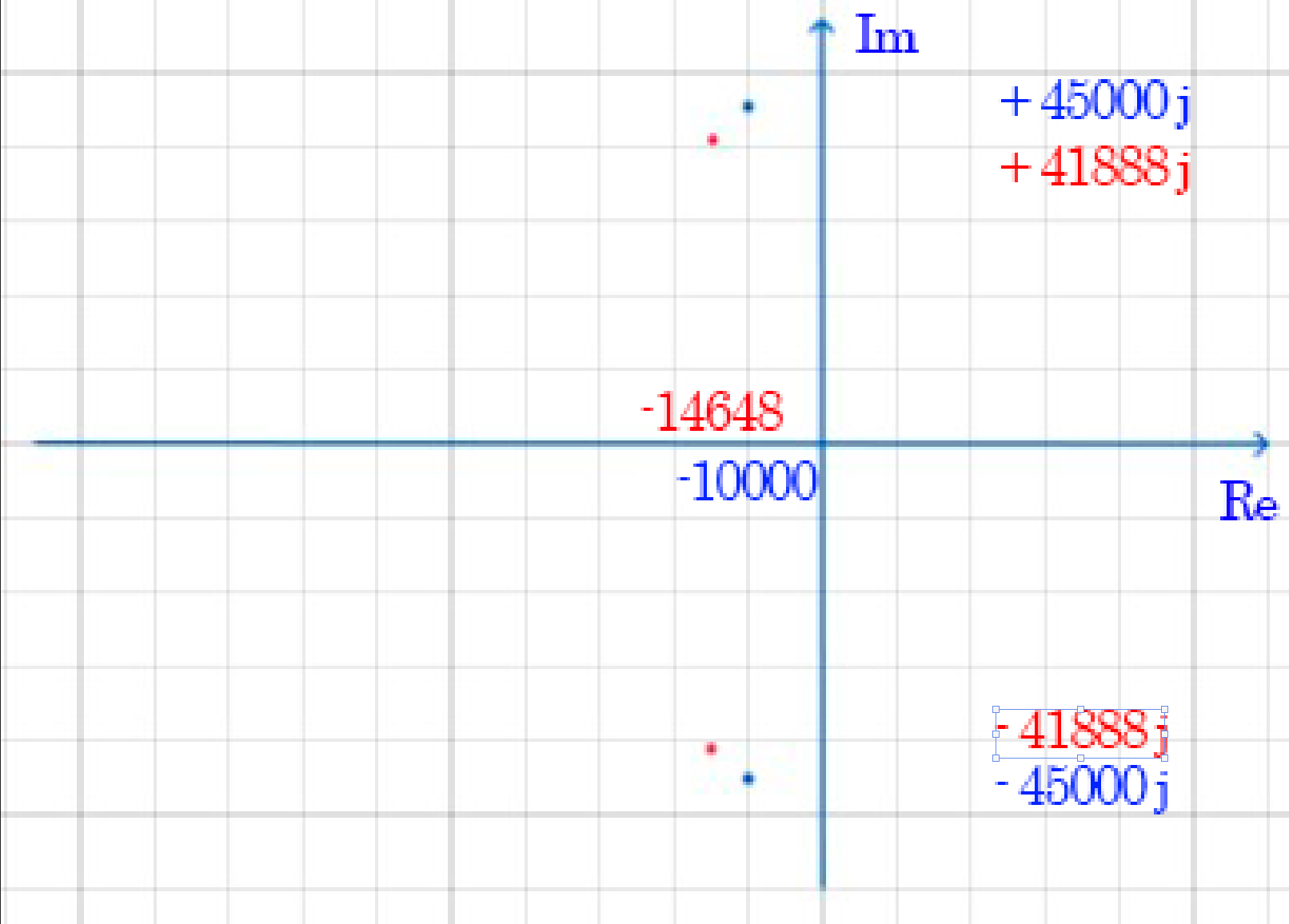
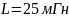
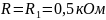
Корни (собственные частоты): p_1,2 = -α ±

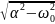
Теоретически:

α₁ = R₁/(2L) = 0,5*10³/(2*25*10^-3)=10000

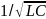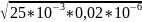= =1/ =4,5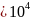

По осциллограмме 2:

;

;

;

;

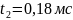α = = ≈ 14648

ω = ≈ 41888

Комплексно-сопряженные корни (колебательный режим) (рис. 5):

p_1,2 ≈ -10⁴ ± j4,5*10⁴

Добротность:

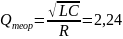
Осциллограмма 3

Корень (собственная частота) на комплексной плоскости – рисунок 6

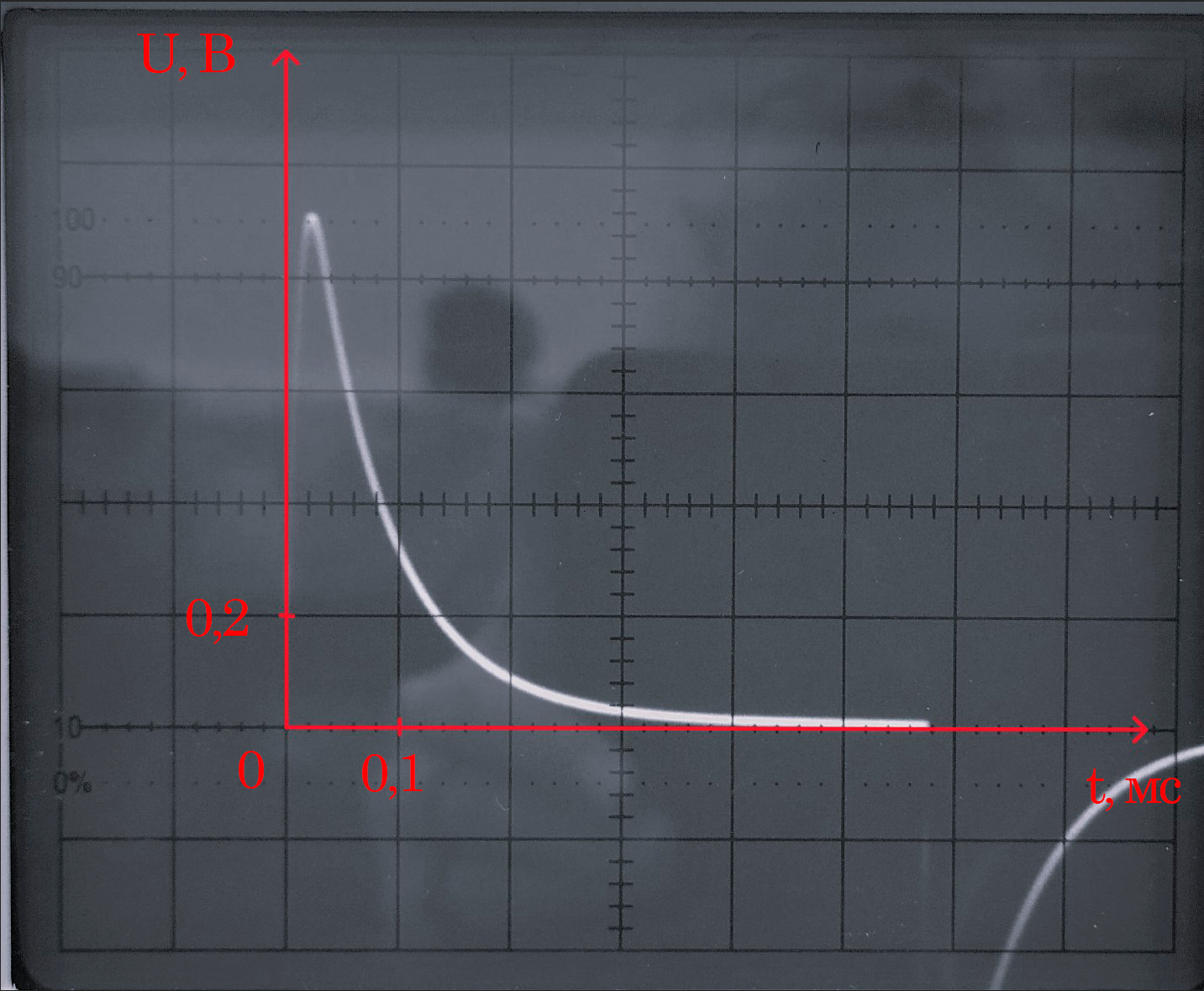
б) Апериодический режим

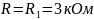
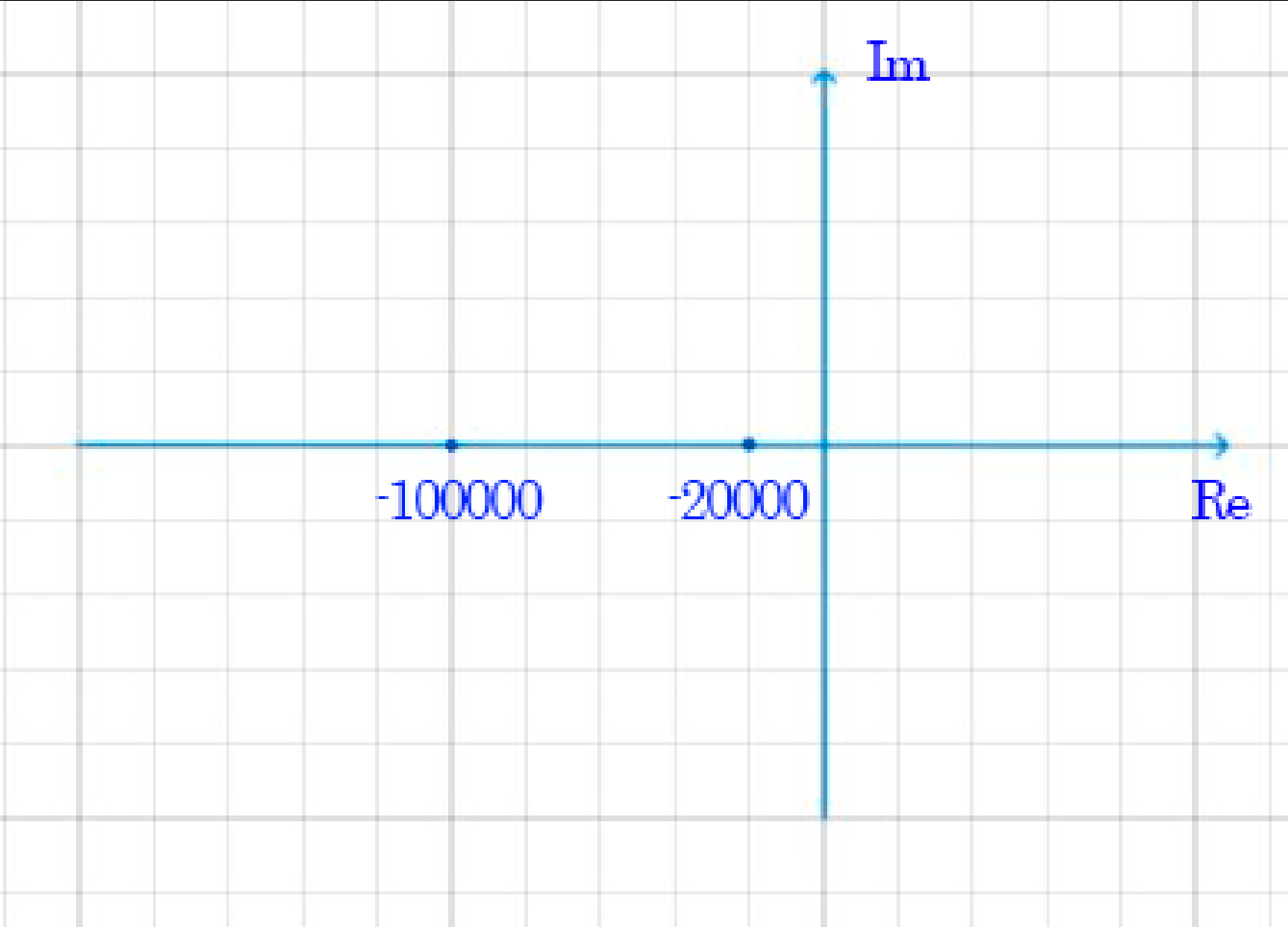
Корни (собственные частоты): p_1,2 = -α ±

α₁ = R₁/(2L) = 3*10³/(2*25*10^-3)= 6

= =1/ =4

Вещественные корни (апериодический режим)

(рис. 6):

p_1,2 ≈ -6*10⁴ ± 4*10⁴;

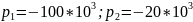
Добротность:

Осциллограмма 4

Корень (собственная частота) на комплексной плоскости – рисунок 7

в) Критический режим:

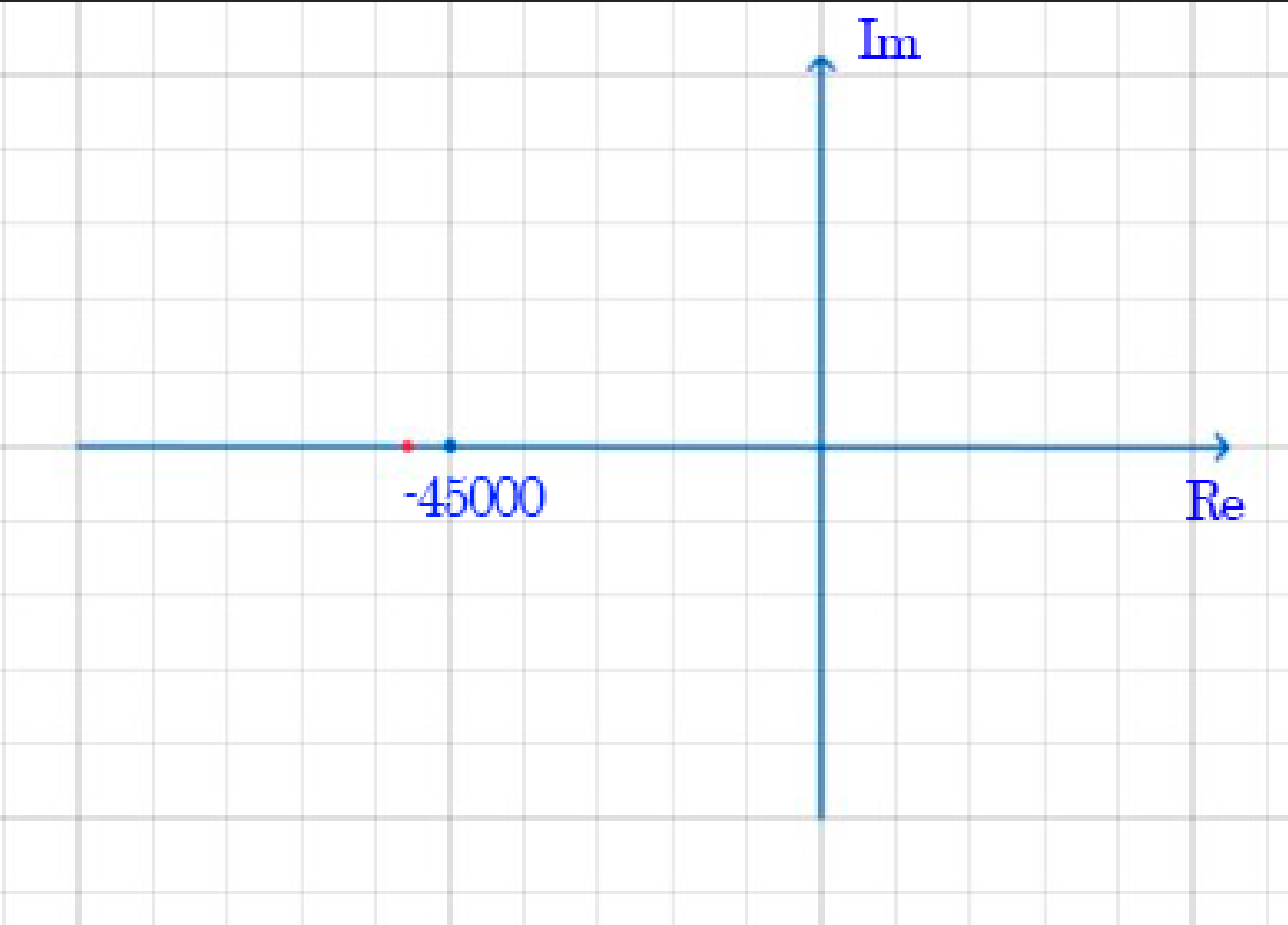
Корни (собственные частоты): p_1,2 = -α ±

Теоретически:

α₁ = R₁/(2L) = 1,8*10³/(2*25*10^-3)= 3,6

= =1/ =4,5

α не может быть меньше , значит сопротивление

критического режима определено неправильно.

Корни появятся при сопротивлении от ≈ 2,24 кОм.

Тогда будет α₁=

По осциллограмме 4:

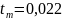
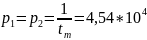
p_1,2 ≈ -4,5 ± j2,7*10⁴

или

Кратные корни (критический режим) (рис. 7):

p_1,2 ≈ -4,5 ± 0*10⁴;

(При )

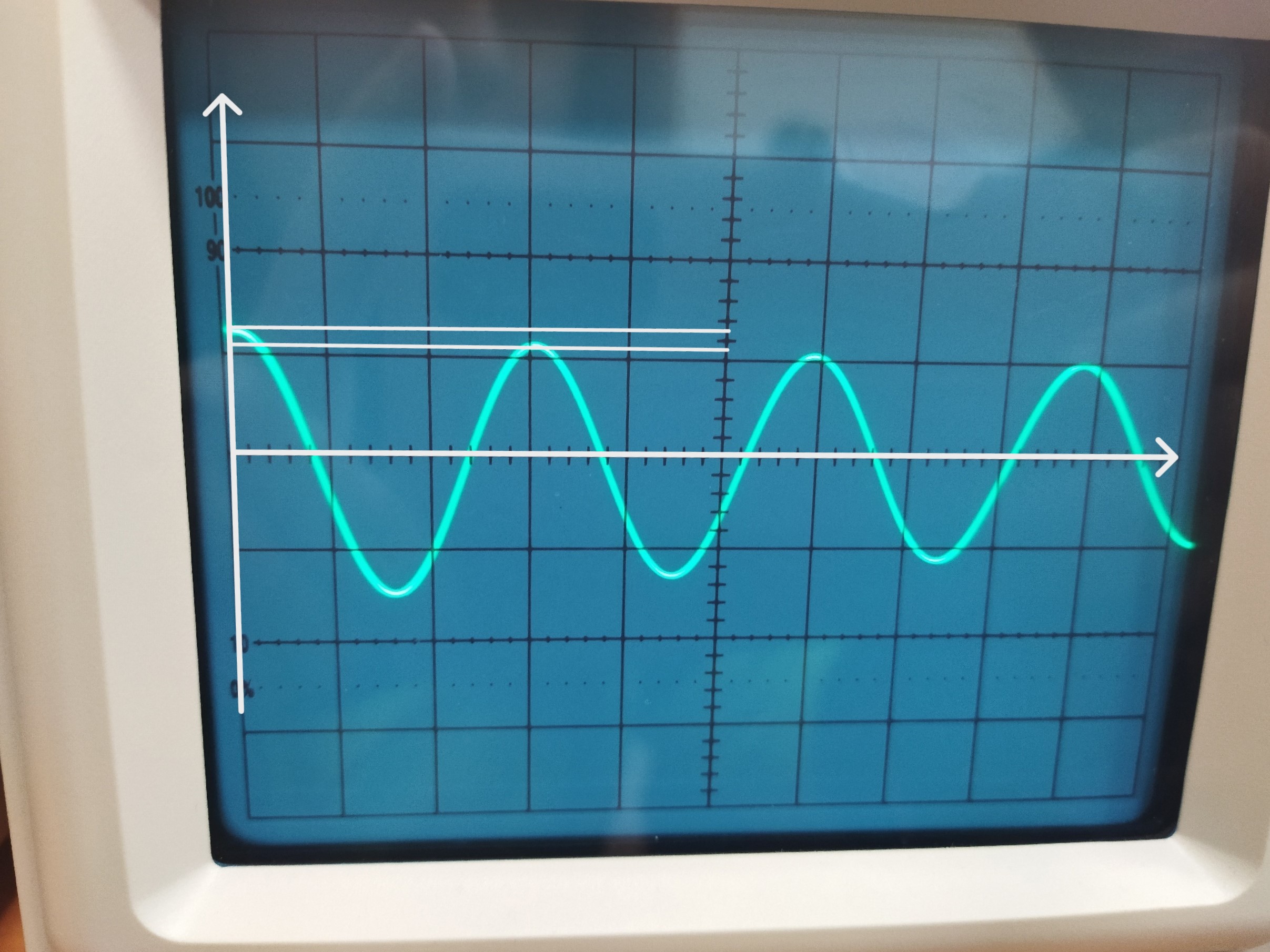
Осциллограмма 5

Корень (собственная частота) на комплексной плоскости – рисунок 8

г) Колебательный незатухающий режим:

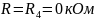
Корни (собственные частоты): p_1,2 = -α ±

Теоретически:

α₁ = R₄/(2L) = 0*10³/(2*25*10^-3)= 0

= =1/ =4,5

По осциллограмме 5:

;

;

;

;

α = = ≈ 14648

ω = ≈ 41888

Комплексно-сопряженные корни (колебательный режим) (рис. 8):

p_1,2 ≈ ±-10⁴ * 10⁴j

3. Исследование свободных процессов в цепи третьего порядка.

Осциллограмма 5

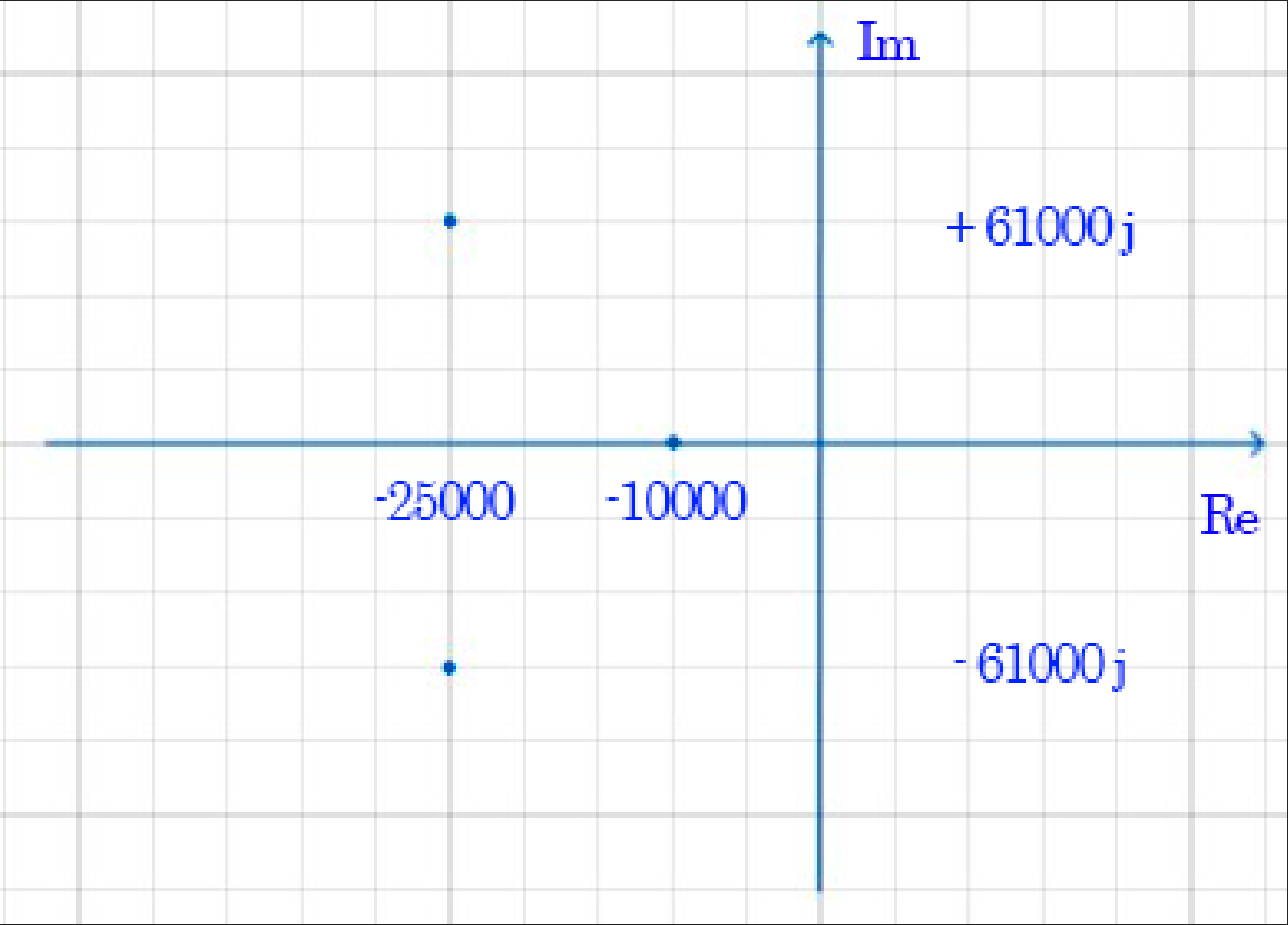
Корень (собственная частота) на комплексной плоскости – рисунок 9

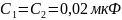
Корни (собственные частоты) (рис. 9):

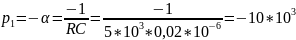
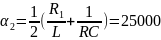
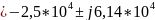
Вывод:

1. При исследовании свободных процессов в цепях первого и второго порядка мы получили небольшие расхождения результатов теоретических расчетов с теми расчетами, которые были получены на основе проведенных экспериментов. В цепи первого порядка ( –11,6 кГц, 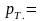– 10 кГц) расхождение немного отличаются. В цепи второго порядка: в колебательном процессе , 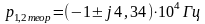) значения не имеют существенных расхождений. Неточные результаты связаны с погрешностью используемых приборов, а также при снятии показаний с осциллографа во время эксперимента. Собственные частоты в апериодическом режиме 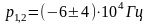. После того, как получили все значения собственных частот, мы расположили их на комплексной плоскости.

2. В критическом режиме было неверно найдено критическое сопротивление. Оно равняется R₁ = 2,25 кОм.

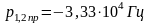
3. Мы убедились в том, что форма реакции цепи зависит от вида ее собственных частот: если собственные частоты вещественные — наблюдается апериодический режим, комплексно-сопряженные — колебательный режим, кратные — критический апериодический режим. Мы вычислили добротность ( ) контура при R=0.5 кОм, что соответствует колебательному режиму. С учетом погрешности добротность равна теоретическому значению .

Вопрос 1. Каким аналитическим выражением описывается осциллографируемый процесс?

Осциллографический процесс имеет экспоненциальный вид, он описывается .

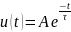Вопрос 2. Соответствует ли найденная собственная частота теоретическому расчету?

Найденная собственная частота отклоняется от теоретического расчета на 10%. Возможно, стоило выбрать для расчета точки, которые точнее указывают значения напряжения и времени.

Вопрос 3. Какими аналитическими выражениями (в общем виде) описываются процессы во всех четырех случаях?

Апериодический режим:

Колебательный режим:

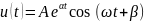
Критический режим:

Незатухающий режим:

Вопрос 4. Соответствуют ли найденные собственные частоты теоретическому расчету?

Найденные собственные частоты соответствуют теоретическому расчету, с учетом погрешности.

Вопрос 6. Как соотносятся найденные значения добротности с результатами теоретического расчета?

Добротность при R₁=0.5 кОм, экспериментальная Q=1.43, теоритическая Q=2.24 (Q>0,5 –колебательный режим)

Вопрос 7. Каким аналитическим выражением описывается осциллографируемый процесс?

Аналитическое выражение для данного процесса: