Лабы / lab3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государтвенный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №3

по дисциплине «Теоретические основы электроники»

Тема: ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Студент гр. 1205		Горбатенко А.Е.
Преподаватель		Евдакова Е.Г

Санкт-Петербург

2023

Цели работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Основные теоретические положения.

В работе предлагается исследовать свободные процессы в цепях, схемы которых представлены на рис. 1. Цепи возбуждаются короткими импульсами тока i₀(t), заряжающими конденсатор C. В паузах между импульсами конденсатор разряжается; цепь находится в свободном режиме, так как в это время источник возбуждения отключен (i₀=0). Поведение линейных цепей описывается линейными дифференциальными уравнениями; при этом вид свободного процесса определяется корнями p_k характеристического уравнения (собственными частотами цепи).

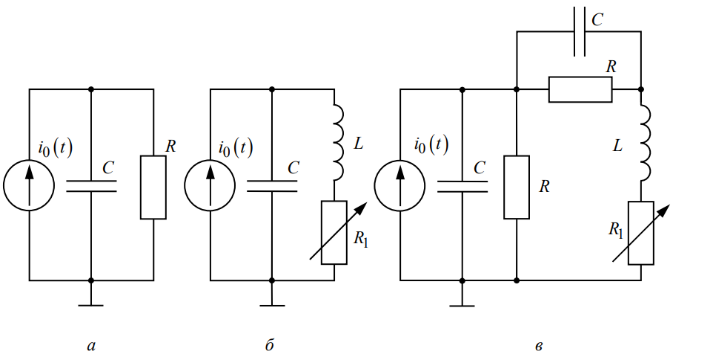
Рис. 1

При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости цепи Y(p), т.е. как корни уравнения Y(p) = 0.

Для цепи первого порядка, представленной на рис.1, а, 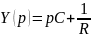, откуда

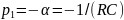
Для цепи второго порядка, изображенной на рис.1, б, 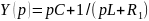,откуда

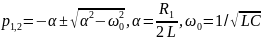
Для цепи третьего порядка, представленной на рис.1, в,

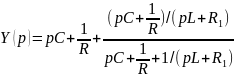
откуда

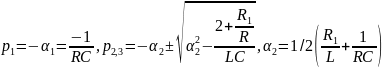
У цепи первого порядка одна собственная частота, вещественная и отрицательная; свободный процесс описывается затухающей экспонентой:

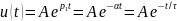
У цепи второго порядка две собственные частоты могут быть вещественными (простыми или кратными) или комплексно-сопряженными. В случае вещественных простых собственных частот

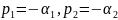
свободный процесс описывается суммой двух экспонент:

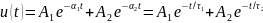
и называется апериодическим. Временная диаграмма процесса для случая

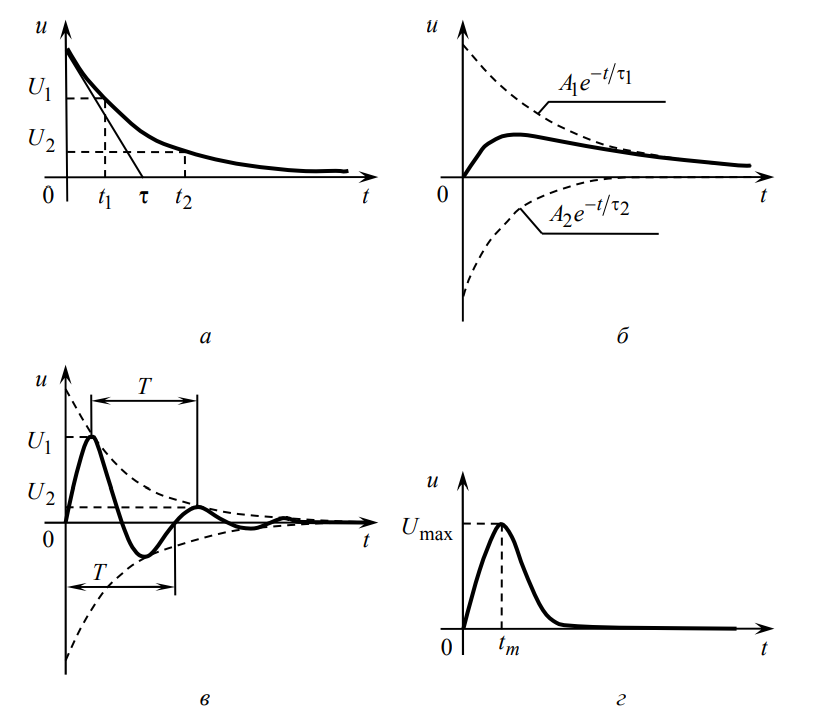
A₁ =- A₂ и 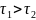приведена на рис.2, б; штрихами показаны отдельные составляющие процесса.

Обработка результатов.

1. Исследование свободных процессов в цепи первого порядка.

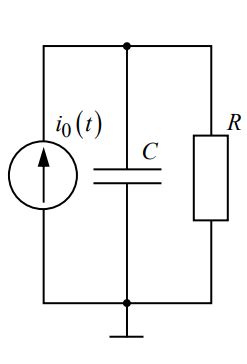
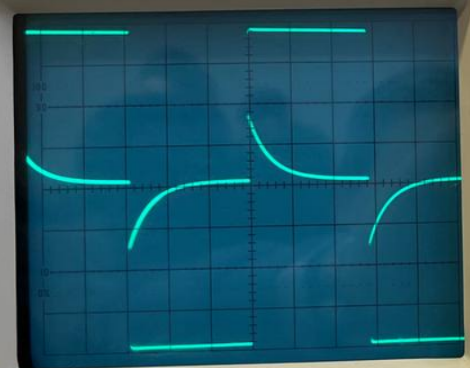
Схема 1 Осциллограмма 1

Теоретическая собственная частота цепи:

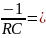
p₁ = 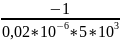= -10 000 с^-1 = -10⁴ с^-1

Собственная частота цепи по осциллограмме:

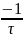p₁= -α = ; α = - 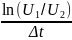= 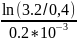≈ - 10397с^-1.

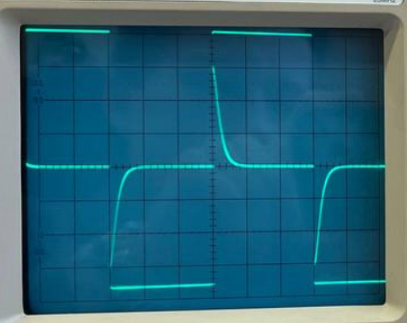2. И сследование свободных процессов в цепи второго порядка.

а) Апериодический режим

p_1,2 = -α ± ;

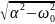α = R₁/(2L) = 3*10³/(2*25*10^-3)=60000.

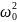= 1/LC=1/( 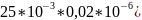=2 *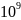

p_1,2 ≈ -(6*10⁴)±3,64*10⁴ с^-1.

б ) Колебательный режим: p_1,2 = -α ± *j;

α = R₁/(2L) = 0,5*10³/(2*25*10^-3)=10000.

= 1/LC=1/( =2*

p_1,2 ≈ -(10⁴)±4,36*10⁴*j с^-1;

Собственная частота цепи по осциллограмме:

p_1,2=-α ± jω= ; α = = 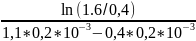≈ 9902,1026 с^-1.

ω = 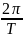≈ 44857,1429 с^-1.

p _1,2 ≈ -0,99*10⁴ ± 4,49*10⁴*j с^-1. в) Критический режим: p_1,2 = -α ± ;

α = R₁/(2L) = 2,25*10³/(2*25*10^-3)=4.5*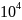

= 1/LC=1/( =2 * p_1,2 ≈ -(4.5*10⁴)±5000 с^-1;

Собственная частота цепи по осциллограмме:

p_1,2=-α = 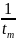= -4,5*10⁴ с^-1.

Добротность контура при колебательном процессе

𝑄 = ω₀/2α = 44857/2*10000 = 2,236

Q =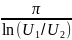 = =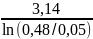 2,27

3)Исследование свободных процессов в цепи третьего порядка.

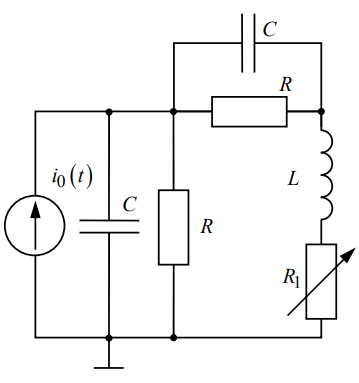
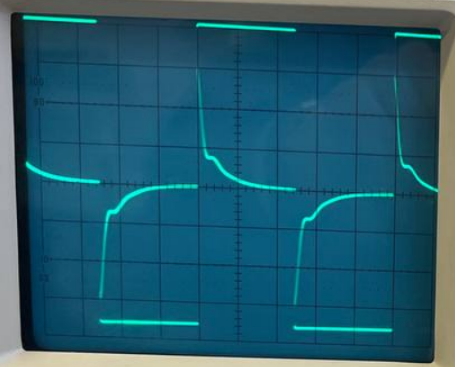
Схема 3 Осциллограмма 6

Расчет теоретического значения собственной частоты контура для цепи третьего порядка:

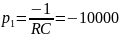
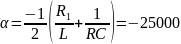
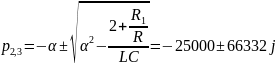
Вывод:

В ходе данной лабораторной работы были рассмотрены свободные процессы в цепях первого, второго и третьего порядка. Практические и теоретические результаты примерно сопоставимы. Было выяснено, что форма реакции цепи зависит от вида ее собственных частот: если собственные частоты вещественные — наблюдается апериодический режим, комплексно-сопряженные — колебательный режим, кратные — критический апериодический режим.

При исследовании свободных процессов в цепях первого и второго порядка мы получили некоторые, незначительные расхождения результатов теоретических расчетов с теми расчетами, которые были получены на основе данных проведенных экспериментов. Эти погрешности можно списать на неточность измерений и человеческий фактор.

Вопрос 1. Осциллографический процесс имеет экспоненциальный вид, он описывается .

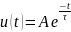Вопрос 2. Да, найденные собственные частоты соответствуют теоретическому расчету,

Вопрос 3. Апериодический режим:

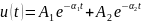
Колебательный режим:

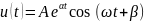
Критический режим:

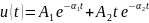
Незатухающий режим:

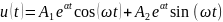
Вопрос 4. Найденные собственные частоты соответствуют теоретическому расчету, с учетом погрешности.

Вопрос 5. При апериодическом режиме собственные частоты равны

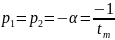
Вопрос 6. Значения добротности удовлетворяют теоретическим расчетам.

Вопрос 7. Аналитическое выражение для данного процесса:

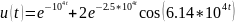
Вопрос8. Собственные частоты соответствуют снятой осциллограмме.

Значения собственных частот, приведены выше.