ph_lab_9

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физики

отчет

по лабораторной работе №9

по дисциплине «Физика»

Тема: Исследование термодинамических циклов

Студент гр. 1205		Агеев А.А.
Преподаватель		Мыльников И.Л.

Санкт-Петербург

2021

Цель работы: исследование политропно-изохорно-изотермического и адиабатно-изохорно-изотермического циклов.

Приборы и принадлежности: баллон с воздухом, манометр, микрокомпрессор, лабораторные термометр и барометр.

Исследуемые закономерности

Определение показателя политропы. Первое начало термодинамики формулируется следующим образом: сообщённое системе количество теплоты расходуется на увеличение внутренней энергии системы и совершение системой работы :

,

где – теплоёмкость газа в изохорном процессе.

-цикл. Процесс расширения воздуха является политропным, в котором теплоёмкость газа С остаётся постоянной. Первое начало термодинамики для политропного процесса имеет вид

или

где C – теплоемкость воздуха в политропном процессе, 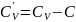. Из этого соотношения с помощью уравнения состояния идеального газа можно получить уравнение Пуассона для политропного процесса или , где n – показатель политропы, где и –теплоемкости газа в изобарном и изохорном процессах.

SVT-цикл. Предположим, что процесс расширения воздуха является адиабатным. Адиабатный процесс является одним из видов политропных процессов, он происходит без теплообмена с окружающей средой: и теплоемкость газа в этом процессе . Поэтому показатель политропы в этом процессе равен и называется показателем адиабаты. Взаимосвязь между параметрами состояния в адиабатном процессе также описывается уравнениями Пуассона либо объединенным газовым законом.

Показатель политропы может быть определён экспериментально:

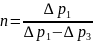
Зная , можно определить мольную теплоемкость газа в политропном процессе

где – показатель адиабаты, равный отношению теплоемкостей газа в изобарном и изохорном процессах, , , – число степеней свободы молекул газа, R=8,31 Дж/(K моль) – универсальная газовая постоянная. Воздух можно считать двухатомным газом, для которого при небольших температурах

Протокол наблюдений

Лабораторная работа № 9

«Исследование термодинамических циклов»

Выполнил студент группы аааааааааа аааааааааааааааааааааааа

Таблица 9.1

p2, Па	V1, л	t1, °С	T1, К

Таблица 9.2

	1	2	3	4	5	6	8	9	10

Работа выполнена «___» _______ 2021 г. __________________

Контрольные вопросы:

1. В каких случаях изменение внутренней энергии системы равно количеству теплоты, подведенному к системе?

В изохорическом процессе, так как в нём работа не совершается.

2. Сформулируйте и выведите закон Бойля-Мариотта , используя основное уравнение кинетической теории газов и уравнение состояния газа.

Обработка результатов.

1. Рассчитаем избыточные давления , P=95%:

Исключим 10 опыт – очевидный промах

2. Рассчитаем показатель политропы на участке 1-2 nVT-цикла:

3. 

4. Начальное состояние:

Состояние 1 (1*):

Состояние 2:

Состояние 2*:

Состояние 3:

Состояние 3*:

Процесс изотермический, тогда

6. Изменения внутренней энергии:

1-2:

2-3:

3-1:

Работа газа:

6. Холодильные коэффициенты для nVT и SVT циклов:

Цикл nVT (1-2-3-1):

Цикл SVT (1-2*-3*-1):

Т.к.

Обратимый цикл Карно:

Для T₁, T₂:

Т.к.

Холодильные коэффициенты циклов Карно меньше холодильных коэффициентов nVT и SVT циклов в сл. Идеальности холодильной машины Карно.

6. Число молей воздуха в сосуде:

6. Мольная теплоемкость при постоянном объеме:

На участке 1-2 воздух охлаждается, а тепло через стеклянную колбу поступает в систему ( ), поэтому теплоёмкость газа в политропном процессе отрицательна

6. Изменение энтропии

nVT (1-2-3-1):

Политропа 1-2:

Политропа 2-3: :

Политропа 3-1: :

Изменение энтропии за цикл:

Вывод: при выполнении лабораторной работы исследованы политропно-изохорно- изотермический (nVT) и адиабатно-изохорно-изотермический (SVT) циклы. С помощью экспериментально измеренных величин избыточных давлений Δp1 и Δp3 определены показатель политропного процесса n, найдены холодильные коэффициенты ε для nVT- и SVT-циклов. С помощью уравнения состояния идеального газа были вычислены параметры состояния (p, V, T). На основе полученных данных построены графики nVT- и SVT-циклов в pV-координатах. Найдены изменения энтропии ΔS для каждого процесса nVT- и SVT-циклов.