
2 лабораторная МОТС
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
отчет
по лабораторной работе №2
по дисциплине «Математические основы теории систем»
Тема: Корреляционный метод измерения задержки сигнала
Студенты гр. 1391 |
|
Поникаровский А. В. Тирик Б. Д. |
Преподаватель |
|
Гульванский В. В. |
Санкт-Петербург
2023
Цель работы: анализ возможностей корреляционных методов выделения сигнала из шума и измерения его параметров.
Теоретические положения.
Корреляция
(correlation), и её частный случай для
центрированных сигналов – ковариация
– это мера схожести двух сигналов.
Приведём один из вариантов использования
корреляционной функции. Допустим, нам
надо найти в тексте некоторый символ.
Скользя по тексту, прикладываем символ
к каждой букве, проверяя их сходство.
Аналогично решается задача обнаружения
некоторой последовательности известной
формы и конечной длины
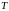 в принимаемом сигнале
в принимаемом сигнале
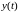 .
.
Для поиска этой
последовательности в скользящем по
сигналу
временном окне длиной
вычисляется интеграл от произведения
процессов
и
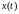 :
:
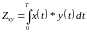
В дискретной форме
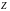 есть скалярное
произведение
векторов
есть скалярное
произведение
векторов
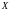 и
и
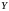 :
: 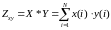
Скалярное
произведение используется как мера
взаимосвязи двух векторов (процессов).
Равенство нулю скалярного произведения
означает крайнюю меру их независимости
– их ортогональность. Чтобы проверить
взаимосвязь векторов при различных
сдвигах одного из них на время
 ,
необходимо
,
необходимо
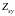 вычислять многократно, для каждого
.
Если ещё ввести нормирующий множитель
вычислять многократно, для каждого
.
Если ещё ввести нормирующий множитель
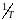 для исключения зависимости
от длины реализации
, получим выражение,
называемое взаимной
корреляционной функцией
(ВКФ):
для исключения зависимости
от длины реализации
, получим выражение,
называемое взаимной
корреляционной функцией
(ВКФ):
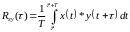 ,
,
Аналогично для случая непрерывного сигнала:
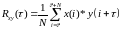
Теперь скалярное произведение превратилось в свёртку двух векторов.
Скалярное
произведения сигнала
с собственной копией,
скользящей по аргументу, а функцию
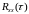 называют автокорреляционной
функцией – АКФ:
называют автокорреляционной
функцией – АКФ:
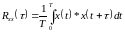 .
.
Автокорреляция позволяет оценить среднестатистическую зависимость текущих отсчётов сигнала от своих предыдущих и последующих значений (так называемый радиус корреляции значений сигнала), а также выявить в сигнале наличие периодически повторяющихся элементов.
В корреляционном анализе часто вид корреляционной функции не имеет значения: интерес представляет один из её параметров. В приведённых выше примерах хотя и вычисляется вся корреляционная функция, однако в первой задаче анализируется только величина максимального значения, а во второй – положение её максимума на временной оси. Для анализа длительности лечебного воздействия прививок в медицине анализируют ширину корреляционной функции, и т.д.
КФ, вычисленная
по центрированному значению сигнала
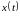 ,
представляет собой ковариационную
функцию сигнала:
,
представляет собой ковариационную
функцию сигнала:
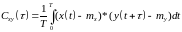
Обработка результатов
1. Создадим излучаемый и принятый импульсы из длинной нулевой последовательности
X = zeros (1,10000);
Y = zeros (1,10000);
X(1:100) = 5;
Y(301:400) = 1;
Посчитаем Rxx(τ) – автокорреляционную функцию и построим её график (рис.1).
conv_R = conv(X,Y);
conv_R = conv_R(1:1000);
plot(conv_R);
title('Автокорреляция одного импульса');
xlabel('Время t');
ylabel('Значение');
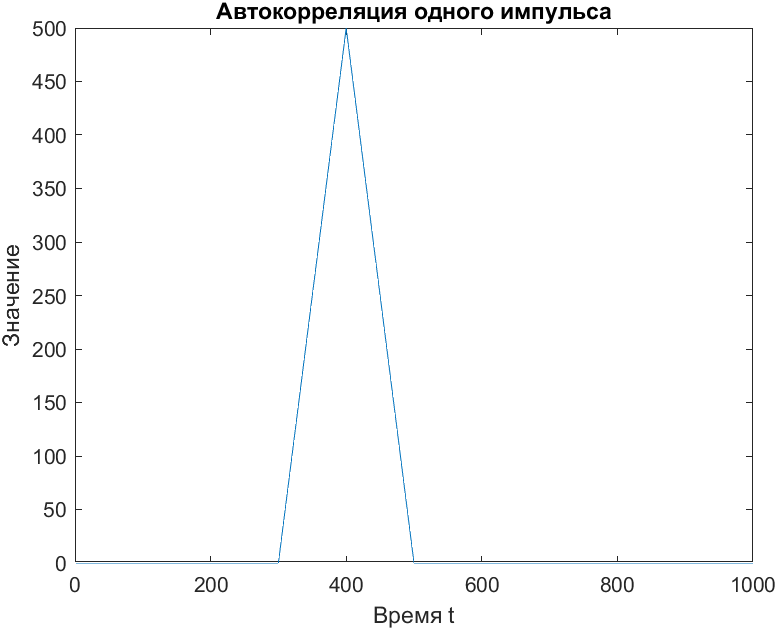
Рис. 1. Автокорреляция одного импульса
Добавим ещё один отправленный и принятый импульс.
X(3500:3600)=5;
Y(3801:4000)=1;
Посчитаем новую Rxx(τ) –корреляционную функцию и построим её график (рис. 2).
xcorr_R = xcorr(X);
figure;
plot(xcorr_R);
xlim([6000 14000]);
ylim([0 5200]);
xticks (6000:1000:14000);
title('Корреляция двух импульсов');
xlabel('Время t');
ylabel('Значение');
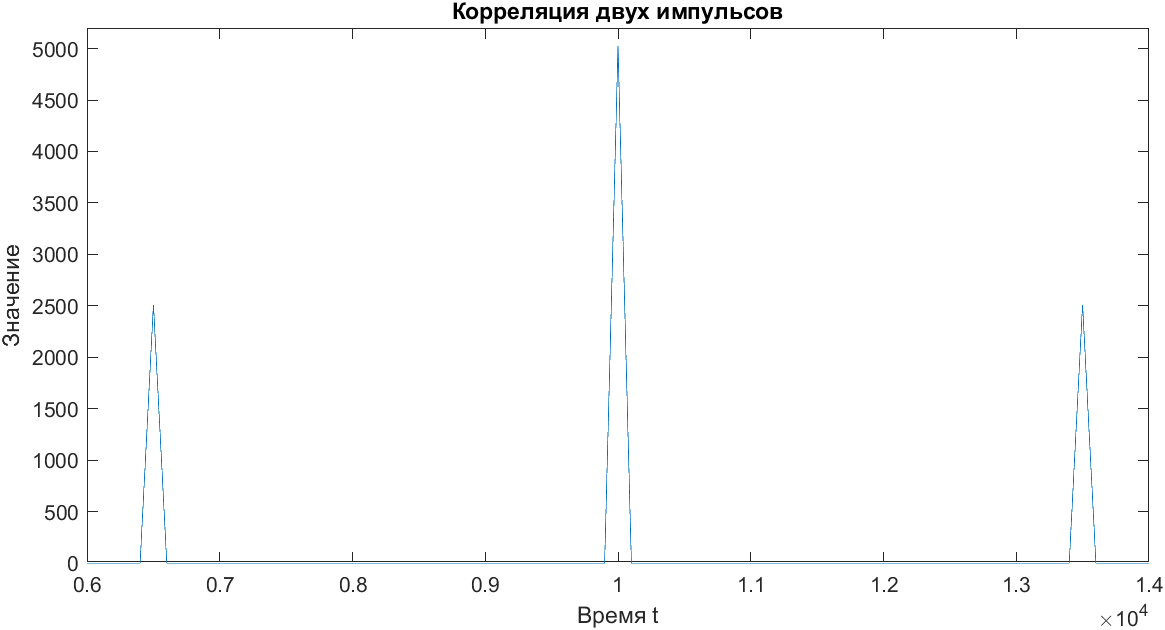
Рис. 2. Корреляция двух импульсов
Первый лепесток – автокорреляция первого импульса, приходящаяся на t = 6500, где первый отправленный и принятый сигналы совпадают.
Пик – корреляция первого и второго сигнала, приходящаяся на t=10000.
Второй лепесток – автокорреляция второго импульса, приходящаяся на t = 13500, где второй отправленный и принятый сигналы совпадают.
2. Создадим ещё более сложный сигнал, в котором нет периодических повторов импульсов и построим его график (рис. 3).
t = 0:0.1:100;
s=3;
p=0;
for i = 1:10
p = p + rectpuls(t-s, 3);
s = s + 5 + 10 * rand;
end
figure;
plot(t,p),grid, set(gca,'FontSize',12);
title('Сигнал без периодичных повторов импульсов');
xlabel('Время t');
ylabel('U');
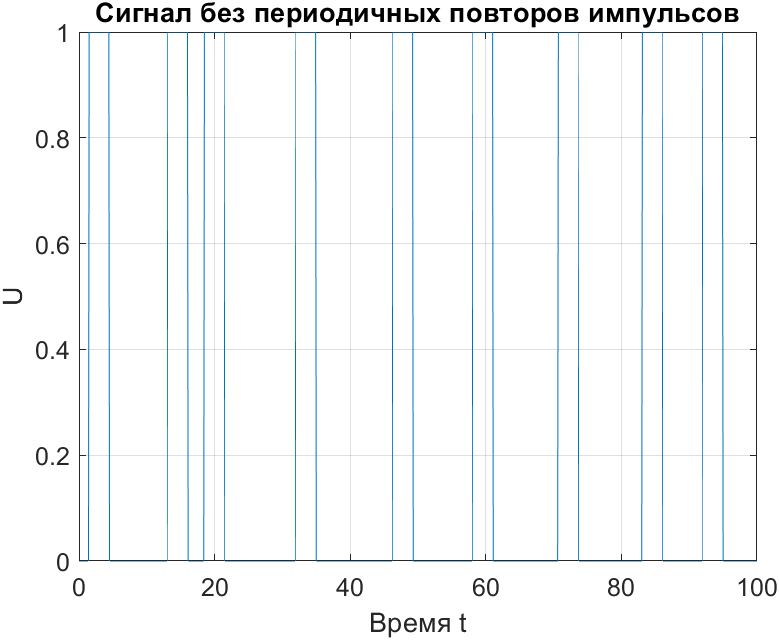
Рис. 3. Сигнал без периодических повторов импульсов
Сымитируем задержку распространения сигнала.
delayed_pulse = zeros(1,300);
delayed_pulse = [delayed_pulse,p];
Вычислим Rxx(τ) и Cxx(τ) и построим их графики (рис. 4 и 5).
xcorr_p = xcorr(p,delayed_pulse);
figure;
plot(xcorr_p);
xlim([0 2000]);
ylim([-20 320]);
title('Корреляция');
xlabel('Время t');
ylabel('Значение');
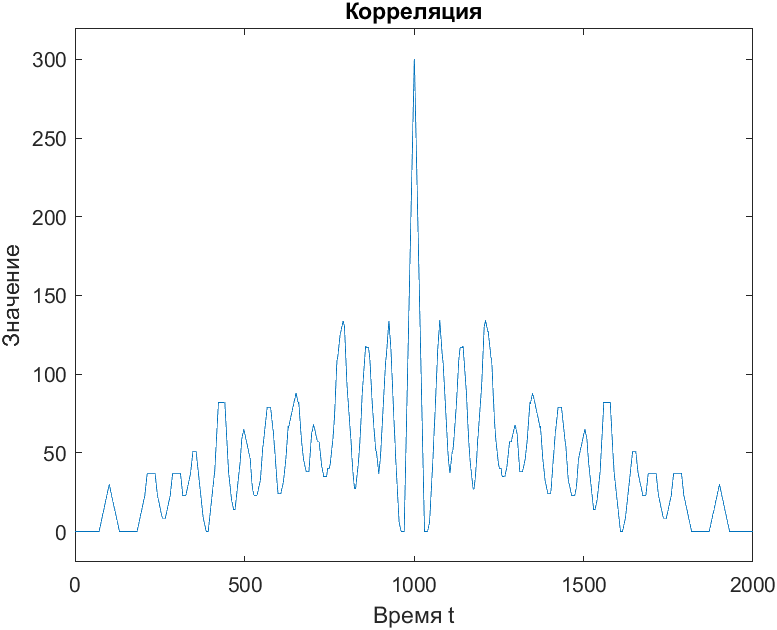
Рис. 4. Корреляция
xcov_p = xcov(p,delayed_pulse);
figure;
plot(xcov_p);
xlim([0 2400]);
ylim([-100 220]);
xticks (0:400:2400);
title('Ковариация');
xlabel('Время t');
ylabel('Значение');
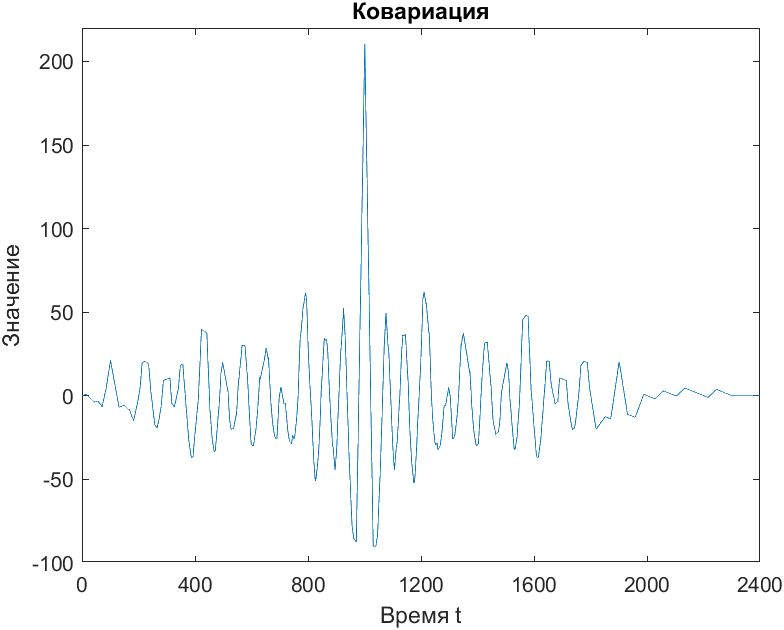
Рис. 5. Ковариация
Отличие связано с тем, что корреляция является мерой схожести сигналов, а ковариация из зависимости между собой.
3. Наложим на принятый (задержанный) сигнал шум с соотношением SNR 3 ÷ 10 дБ и построим график (рис. 6).
figure;
out = awgn(delayed_pulse,0.3);
plot(delayed_pulse, 'LineWidth',3);
hold on;
plot(delayed_pulse+out);
legend('Меандр','Меандр с шумом');
title('Сигнал без периодичных повторов импульсов c шумом');
xlabel('Время t');
ylabel('U');
hold off;
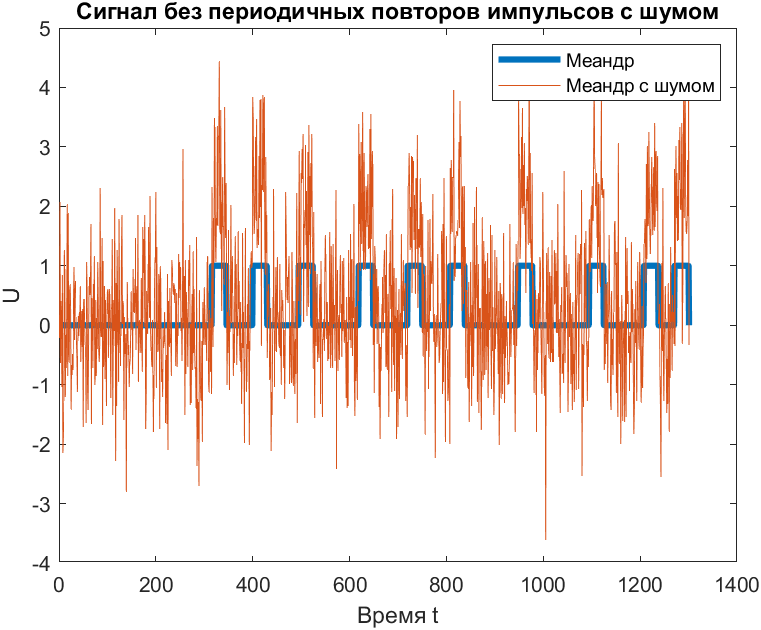
Рис. 6. Сигнал без периодичных повторов импульсов c шумом
Опытным путём выяснилось, что минимальное значение, при котором ещё возможно измерение задержки, равно 1.5 (рис. 7).
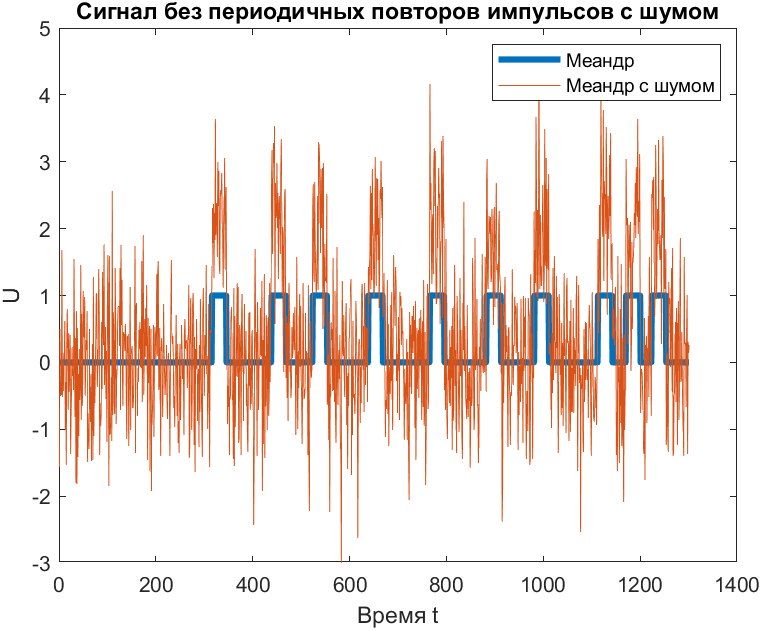
Рис. 7. Сигнал c шумом и значением SNR 1.5
4. В качестве посылаемого сигнала возьмём отрезок синусоиды.
f = 2;
t = 1:0.01:5;
sin_x = sin(2*pi*f*t);
Наложим шум и построим графики (рис.8).
figure
hold on
plot(t,sin_x, 'LineWidth',3);
sin_x_noise = awgn(sin_x, 10);
plot(t,(sin_x+sin_x_noise));
legend('Синусоида','Синусойда с шумом');
title('Синусоида с шумом');
xlabel('Время t');
ylabel('U');
hold off;
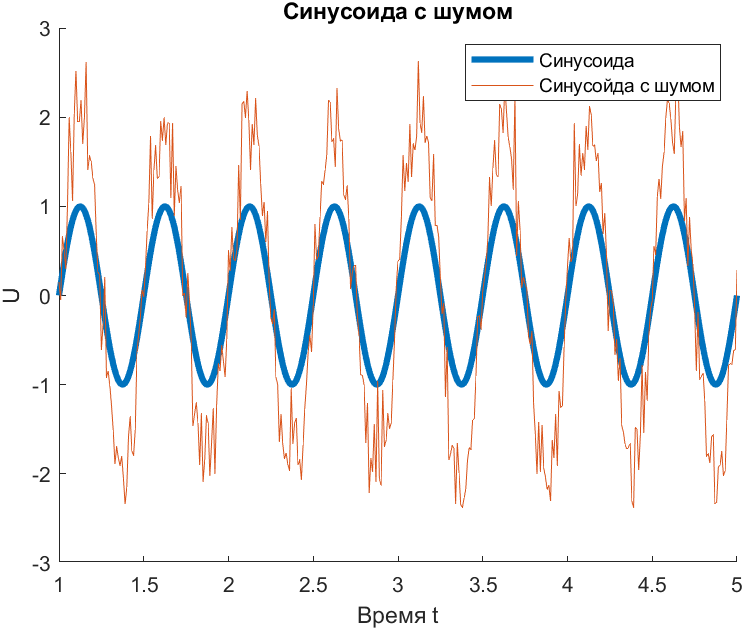
Рис. 8. Синусоида с шумом
t=1:0.01:9;
xcorr_R3 = xcorr(sin_x,(sin_x+sin_x_noise));
figure
plot(t,xcorr_R3),grid;
title('Корреляция');
xlabel('Время t');
ylabel('Значение');
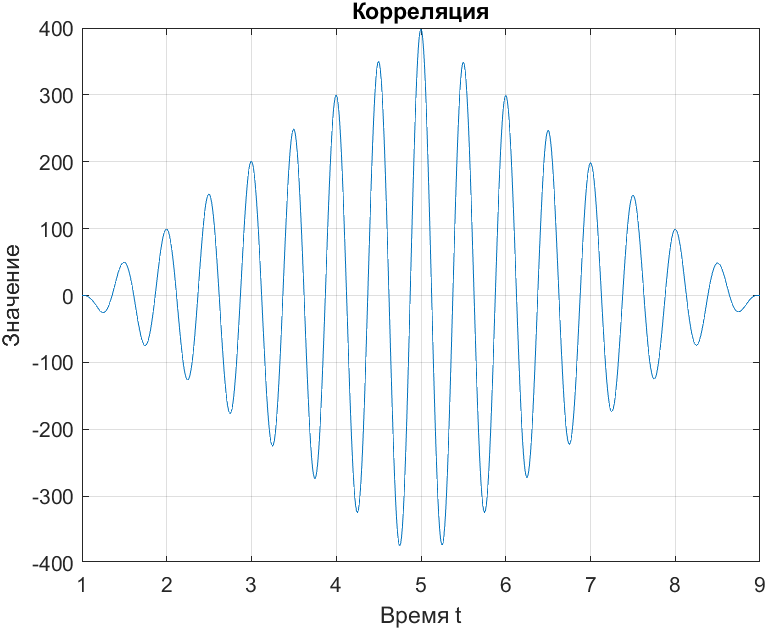
Рис. 9. АКФ синусоиды с шумом
Чтобы найти задержку на функции корреляции необходимо найти t при котором будет наибольшее значение функции корреляции. В данном случае при t=5 будет максимальное значение АКФ (рис. 10).
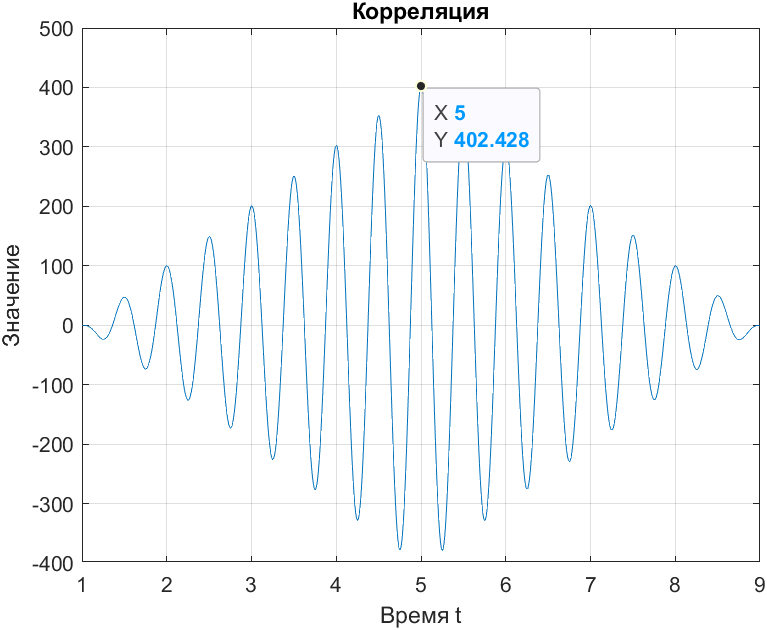
Рис. 10. Задержка АКФ
5. Построим сигнал с помощью кода Баркера и наложим на него шум, и выведем его график (рис. 11).
barker = comm.BarkerCode('Length',13,'SamplesPerFrame',13);
Bar = barker();
Bar = Bar';
t = 0:(length(Bar)*13) - 1;
s0 = square(t);
s(1:169)=0;
for j=1:13
for i=1:13
s(:,i*j) = s0(:,i*j)*Bar(j);
end
end
figure
hold on
plot(t, s,'red', 'LineWidth',1.5);
w_noise = awgn(s,10);
plot(t,w_noise,'blue');
legend('Код Баркера','Код Баркера с шумом');
title('Код Баркера');
xlabel('Время t');
ylabel('U');
hold off
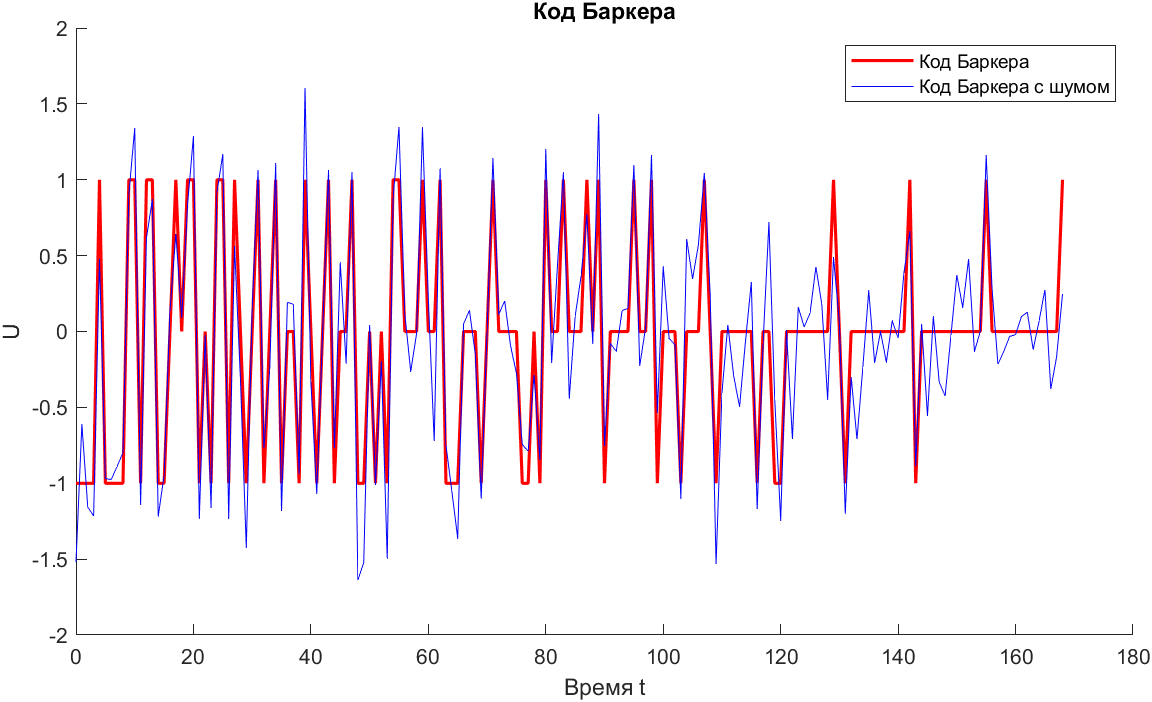
Рис. 11. Код Баркера
Построим шумоподобный (rand) сигнал (рис.12).
K=0:1:13;
X=randi([-1,1],1,14);
w_noise2 = awgn(X,10);
figure
hold on
plot(K,X,'g'), grid;
plot(K,w_noise2,'r'), grid;
legend('Шумоподобный сигнал','Шумоподобный сигнал с шумом');
xlabel('Время t');
ylabel('U');
hold off;
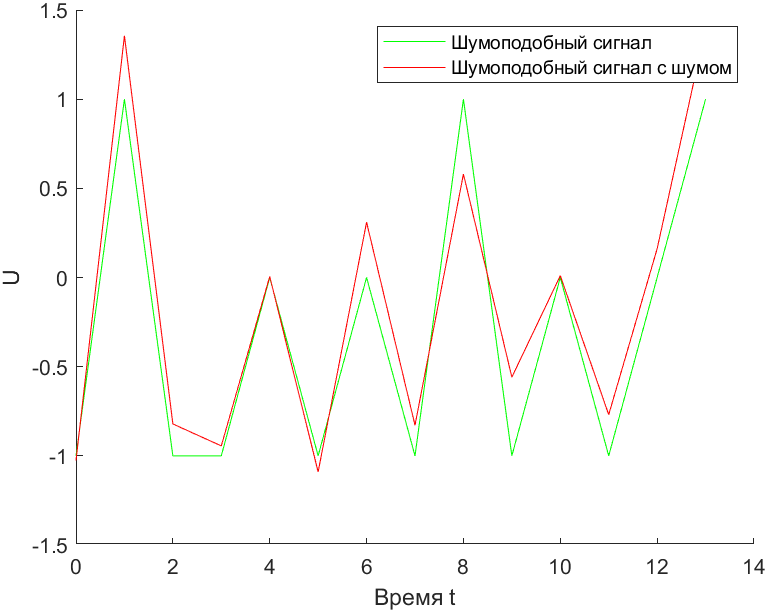
Рис. 12. Шумоподобный сигнал
Посчитаем автокорреляционную функцию и построим график для обоих сигналов.
Для кода Баркера (рис.13).
xcorr_R4 = xcorr(Bar);
plot(xcorr_R4), grid;
title('Автокорреляция');
xlabel('Время t');
ylabel('Значение');
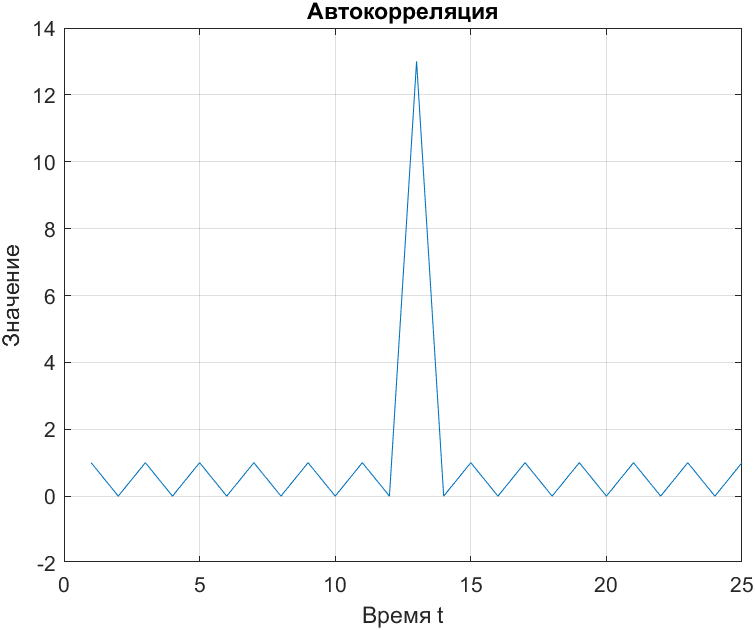
Рис. 13. АКФ для кода Баркера
Для шумоподобного сигнала (рис.14).
R5=xcorr(X);
plot(R5), grid;
title('Автокорреляция');
xlabel('Время t');
ylabel('Значение');
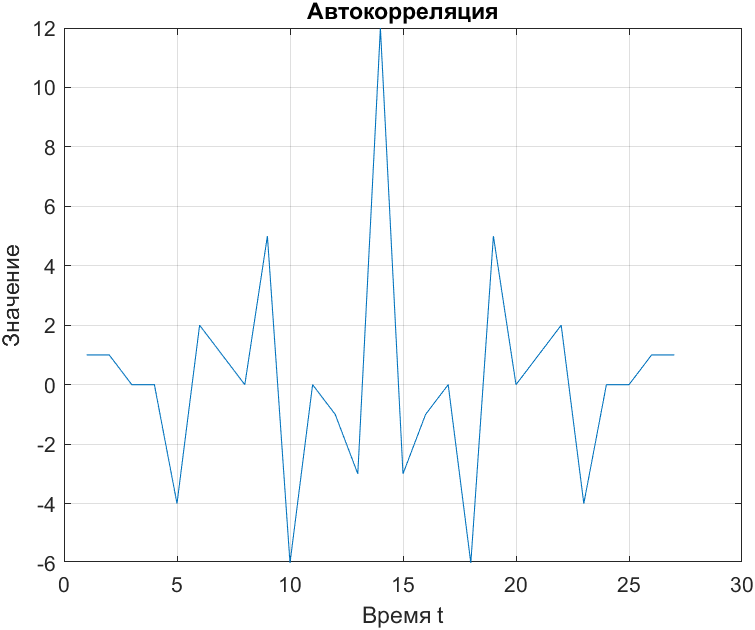
Рис. 14. АКФ для шумоподобного сигнала
6. Повторим пункт 3, где в качестве сигнала используем код Баркера и шумоподобный сигнал.
Наложим на код Баркера шум и построим график (рис. 15).
barker = comm.BarkerCode('Length',13,'SamplesPerFrame',13);
Bar = barker();
Bar = Bar';
t = 0:(length(Bar)*13) - 1;
s0 = square(t);
s(1:169)=0;
for j=1:13
for i=1:13
s(:,i*j) = s0(:,i*j)*Bar(j);
end
end
figure
hold on
plot(t, s,'red', 'LineWidth',1.5);
w_noise = awgn(s, 12.5);
plot(t,w_noise,'blue');
legend('Код Баркера','Код Баркера с шумом');
title('Код Баркера');
xlabel('Время t');
ylabel('U');
hold off
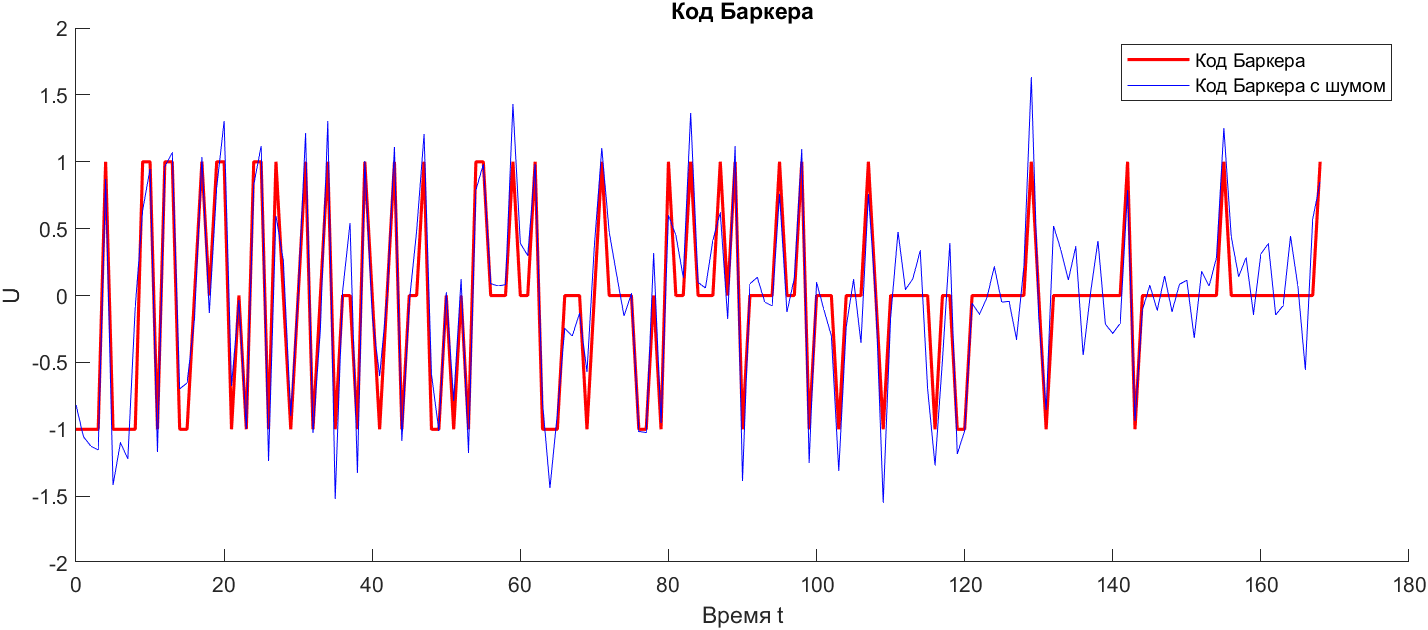
Рис. 15. Код Баркера c шумом и значением SNR 12.5
Опытным путём выяснилось, что минимальное значение, при котором ещё возможно измерение задержки, равно 12.5.
Наложим на шумоподобный сигнал шум и построим график (рис. 16).
K=0:1:13;
X=randi([-1,1],1,14);
w_noise2 = awgn(X,11);
figure
hold on
plot(K,X,'g'), grid;
plot(K,w_noise2,'r'), grid;
legend('Шумоподобный сигнал','Шумоподобный сигнал с шумом');
xlabel('Время t');
ylabel('U');
hold off;
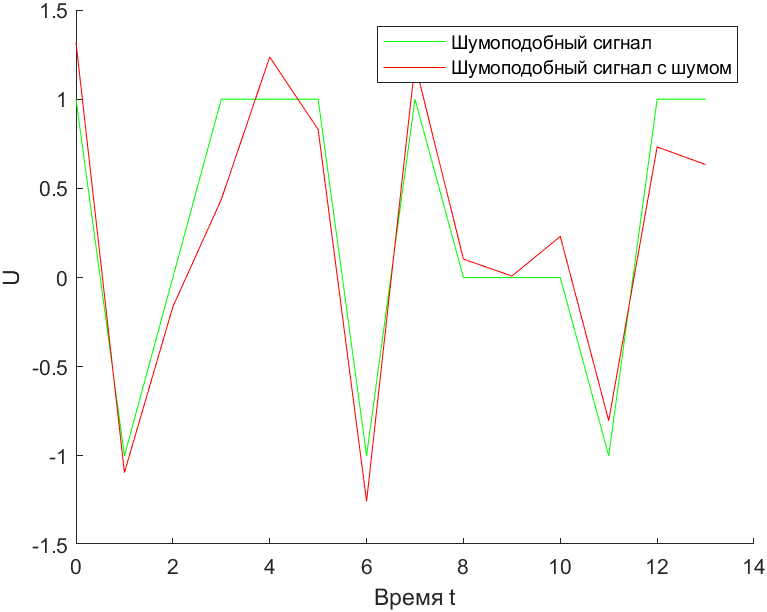
Рис. 16. Шумоподобный сигнал c шумом и значением SNR 11
Опытным путём выяснилось, что минимальное значение, при котором ещё возможно измерение задержки, равно 11.
7. Найдём E (мат. ожидание), σ, σ2
t =0:1:10000;
fn = 100;
fc = 1;
m = 0.5;
Моногармонический:
mono = sin(2*pi*fc*t);
mat1 = mean(mono);
dispers1 = var(mono);
dispers12 = dispers1^(1/2);
histogram(mono);xlabel('Моногармонический');grid on;
E = -1.898861239877101e-15
σ = 1.109024494078334e-24
σ2 = 1.053102318902743e-12
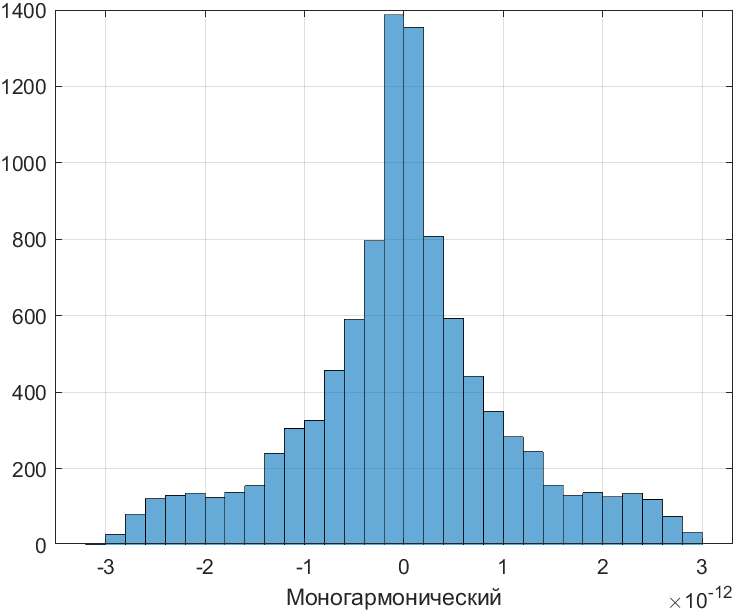
Рис. 17. Гистограмма моногармонического сигнала
C линейной частотой модуляцией:
lin = sin(2*pi*fc*t.^2);
mat2 = mean(lin);
dispers2 = var(lin);
dispers22 = dispers2^(1/2);
histogram(lin);xlabel('С линейной частотой модуляцией');grid on;
E = 2.664439078993618e-11
σ = 8.036504472626515e-17
σ2 = 8.964655304375353e-09
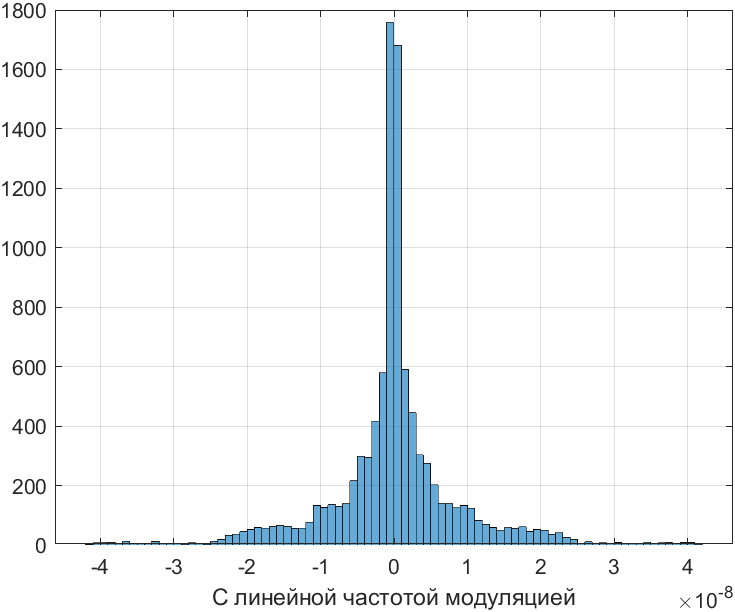
Рис. 18. Гистограмма сигнала с линейной частотой модуляцией
С амплитудной модуляцией:
ampl = sin(2*pi*fn*t).*(1+m*sin(2*pi*fc*t));
mat3 = mean(ampl);
dispers3 = var(ampl);
dispers32 = dispers3^(1/2);
histogram(ampl);xlabel('С амплитудной модуляцией');grid on;
E = 1.942666751642201e-11
σ = 3.105715327679667e-20
σ2 = 1.762303982767918e-10
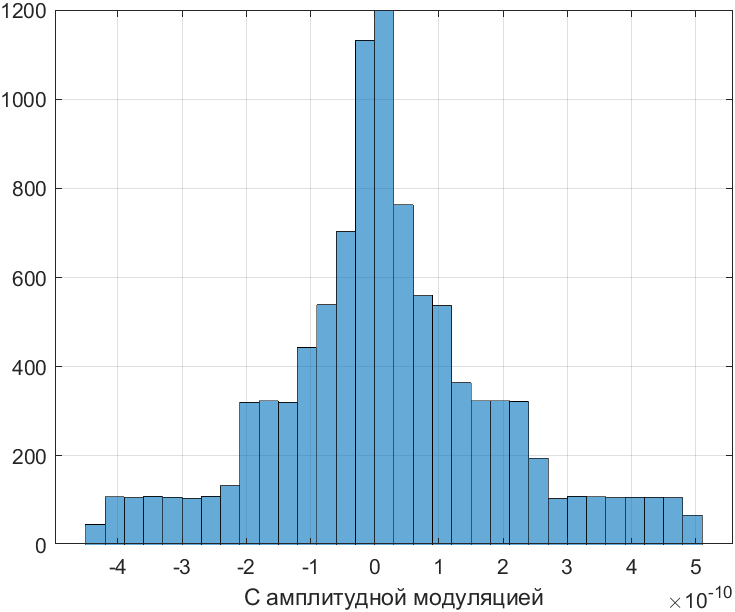
Рис. 19. Гистограмма сигнала с амплитудной модуляцией
С частотной модуляцией:
chastot = sin(2*pi*fc*(cos(0.5*t)).*t);
mat4 = mean(chastot);
dispers4 = var(chastot);
dispers44 = dispers4^(1/2);
histogram(chastot);xlabel('С частотной модуляцией');grid on;
E = 0.002175707813835
σ = 0.494195349556964
σ2 = 0.702990291225252
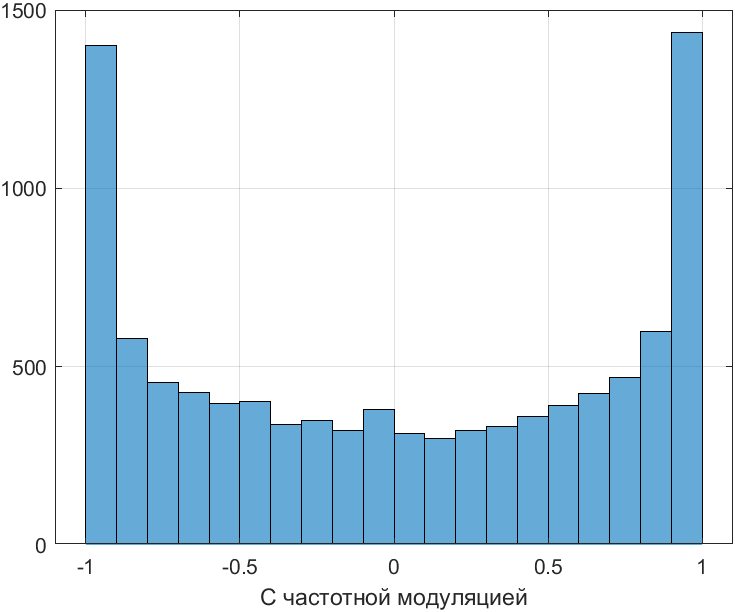
Рис. 20. Гистограмма сигнала с частотной модуляцией
С фазовой модуляцией:
phase = sin(2*pi*fn*t+5*sin(2*pi*t));
mat5 = mean(phase);
dispers5 = var(phase);
dispers55 = dispers5^(1/2);
histogram(phase);xlabel('С фазовой модуляцией');grid on;
E = 1.942666751642212e-11
σ = 3.105715327679660e-20
σ2 = 1.762303982767916e-10
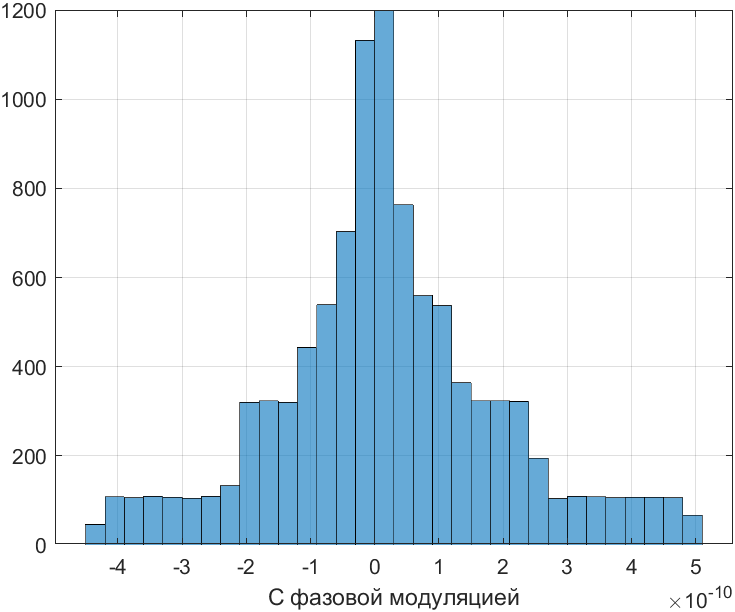
Рис. 21. Гистограмма сигнала с фазовой модуляцией
Вывод
Мы проанализировали возможности корреляционных методов выделения сигнала из шума и измерения его параметров. Построили различные сигналы, на которые были наложены шумы, также абстрактные сигналы: шумообразный сигнал, сигнал на основе кода Баркера и т.п. Для этих сигналов было изучено поведение корреляции и автокорреляции. Также были изучены различные виды сигналов и модуляции, их математическое ожидания, дисперсии, также для них построены гистограммы.
