МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №3

по дисциплине «Математические основы теории систем»

Тема: Спектр. Ряд Фурье

Студентка гр. 9391		Мысик А.С.
Студентка гр. 9391		. Сингх Н.Д
Студент гр. 9391		Фазекаш В.В.
Преподаватель		Гульванский В.В.

Санкт-Петербург

2021

Цель:

• Знакомство со спектральным представлением периодических и случайных процессов;

• Изучение взаимосвязи преобразований сигналов во временной и частотной областях;

• Оценка дефектов дискретного преобразования Фурье и методы их подавления.

Ход работы:

1. Создадим два сигнала x1=cos(2*pi*f1*t) x2=4*cos(2*pi*f2*t). Построим их графики (рис. 1). Построим графики модуля спектра сигналов (рис. 2-3).

fs = 200;

dt = 1/fs;

t = 0:dt:1;

f1=20;

f2=3;

x1=cos(2*pi*f1*t);

x2=4*cos(2*pi*f2*t);

plot(t,x1,t,x2,'LineWidth',2); grid on;

title("Сигналы");

xlabel("Частота");

ylabel("Амплитуда");

legend('x1','x2');

R=abs(fft(x1));

figure;

area(t,R), grid;

title("Амплитудный спектр первого сигнала x1");

xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

R=abs(fft(x2));

figure;

area(t,R), grid;

title("Амплитудный спектр второго сигнала x2");

xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

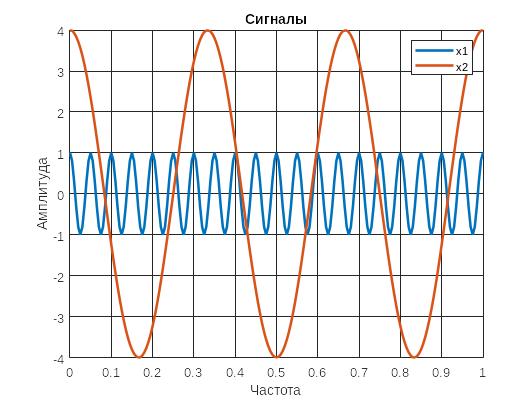
Рисунок 1- Сигналы

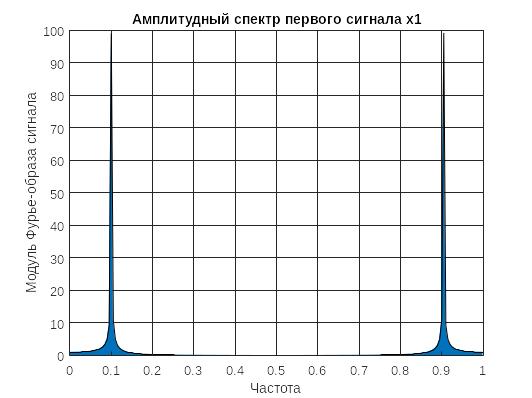
Рисунок 2 - спектр первого сигнала

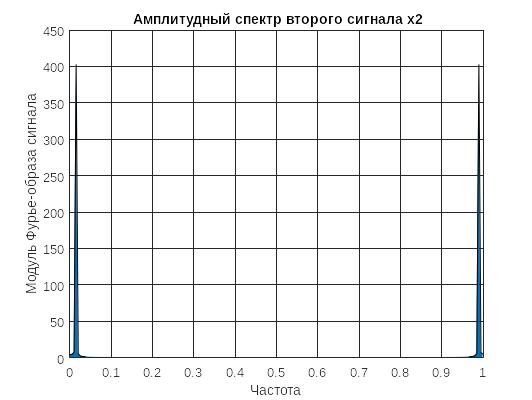
Рисунок 3 - спектр второго сигнала

2. Создадим еще два сигнала x3=x1+x2; x4=x1.*x2. На рисунке 4-5 представлены их спектры.

x3=x1+x2;

x4=x1.*x2;

R=abs(fft(x3));

figure;

area(t,R), grid;

title("Амплитудный спектр третьего сигнала x3");

xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

R=abs(fft(x4));

figure;

area(t,R), grid;

title("Амплитудный спектр четвертого сигнала x4");

xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

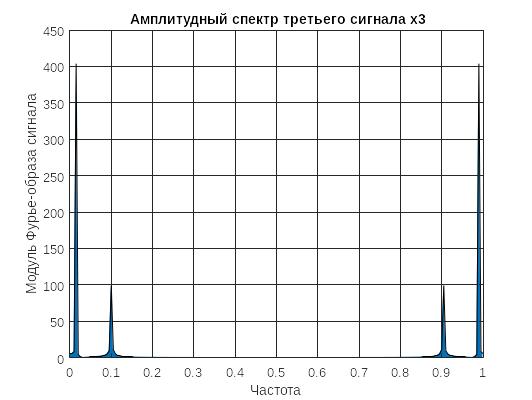
Рисунок 4 - спектр третьего сигнала

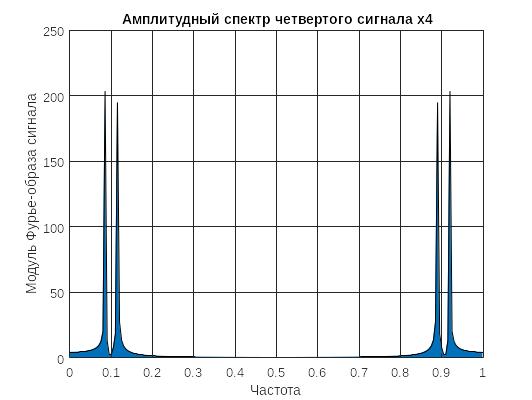
Рисунок 5- спектр четвертого сигнала

Спектры получились различными, в так как при сложении сигналов их частоты и амплитуды на этих частотах сохраняются, а при перемножении сигналов амплитуда на пиках уравнивается, частоты при этом получаются разностные и суммарные.

3. На временном интервале отсчетов создадим -импульс (рис. 6). На рисунке 7 представлены их спектры модуля и фазы соответственно. Сдвинем -импульс. На рисунке 8 представлены их спектры модуля и фазы соответственно. Видим, что спектры одинаковые.

x3=x1+x2;

x4=x1.*x2;

R=abs(fft(x3));

figure;

area(t,R), grid;

title("Амплитудный спектр третьего сигнала x3");

Xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

R=abs(fft(x4));

figure;

area(t,R), grid;

title("Амплитудный спектр четвертого сигнала x4");

Xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

Рисунок 6- функция Дирака

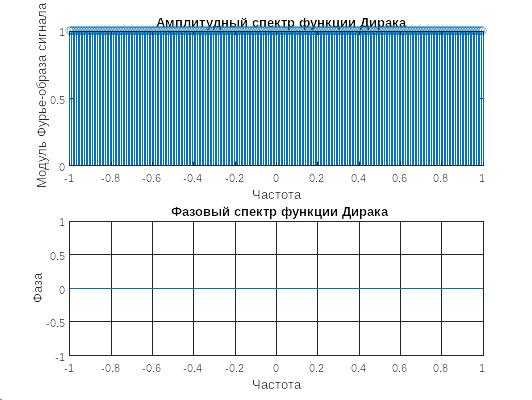
Рисунок 7 - спектры функции Дирака

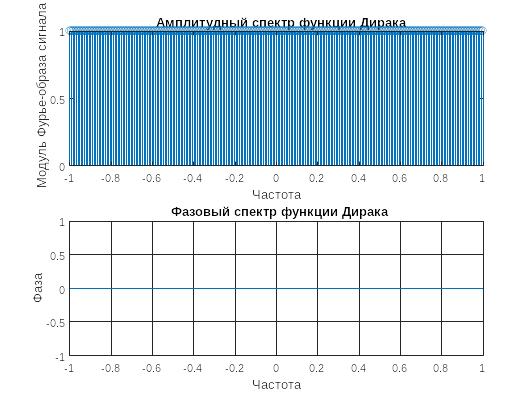
Рисунок 8 - спектры смещенной функции Дирака

4. Последовательно увеличим ширину импульса, наблюдая соответствующие изменения его спектра (рис. 9). Для произвольной ширины импульса рассчитаем спектр вручную (рис. 10).

N=2^7;

t = -1:1/N:1;

y = dirac(t);

idx = y == Inf; % find Inf

y(idx) = 1; % set Inf to finite value

T = 1; % период повторения импульсов

tau = dirac(0); % положение максимума пилообразного импульса

M = 100; % количество рассматриваемых гармоник

k = 1:M; % номера гармоник

w = 2*pi*k/T; % частоты гармоник

% нулевая гармоника (среднее значение сигнала за период)

c1(1) = tau/T;

c1(2:1+M) = 1/T;

f1(1) = 0;

f1(2:1+M) = w/2/pi; % частоты

figure;

stem(f1,abs(c1),'k.')

axis([0 10 0 1]);

title("Амплитудный спектр функции Дирака");

Xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

figure;

for i=1:2:7

y(1,129+i)=1;

R1=abs(fft(y));

R2=phase(y);

subplot(4,2,i),area(t,R1), title("Амплитудный спектр");

Xlabel("Частота");

ylabel("Амплитуда");

subplot(4,2,i+1),plot(t,R2), title("Фазовый спектр");

Xlabel("Частота");

ylabel("Фаза");

end

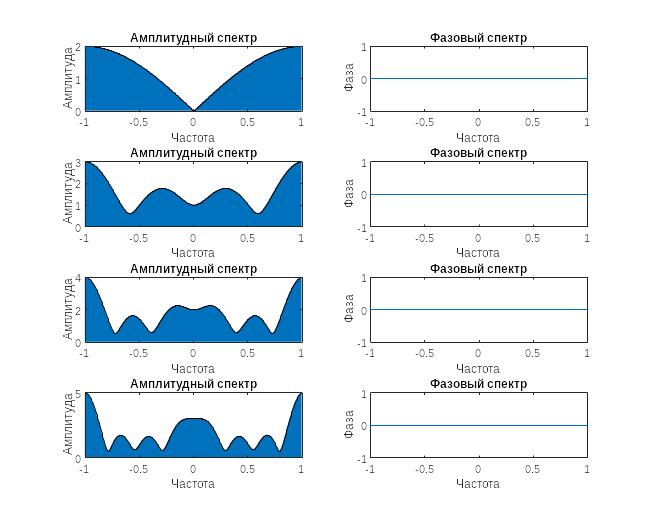
Рисунок 9- спектр функции Дирака при увеличении ширины импульса

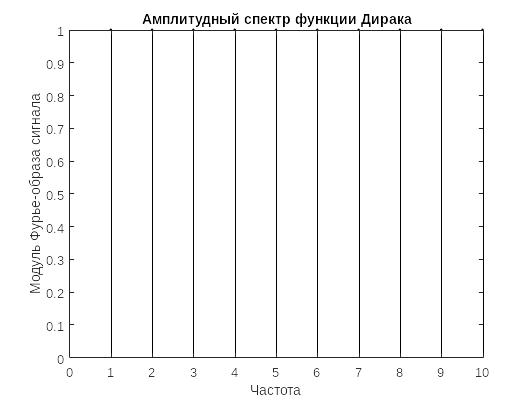
Рисунок 10 - спектр функции Дирака, построенный вручную

Видим, что амплитудный спектр изменяется, фазовая остается неизменным.

5. Построим спектр периодического прямоугольного сигнала со скважностью 2 (меандр) и количеством периодов, кратным двум (рис. 11). На рисунке 12 представлен его спектр. Рассчитаем спектр вручную и построим его график (рис. 13).

N=100;

t = 0:1/N:1;

w = 0.04;

j=0;

imp=0;

for i = 1:10

imp =imp+rectpuls(t-j,w);

j=j+0.08;

end

plot(t,imp);

grid on;

title("Прямоугольный сигнал");

Xlabel("Частота");

ylabel("Амплитуда");

% % % %

T = 10;

tau = 1;

M = 100; % количество рассматриваемых гармоник

k = 1:M; % номера гармоник

w = 2*pi*k/T; % частоты гармоник

% нулевая гармоника (среднее значение сигнала за период)

c1=zeros(1,101);

c1(1) = tau/2;

for k=1:2:M

c1(k+1) = 2*tau/(k*pi);

end

f1(1) = 0;

f1(2:1+M) =w*pi/2; % частоты

figure

stem(f1,abs(c1),'k.')

title("Амплитудный спектр прямоугольного сигнала");

Xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

grid on;

figure;

R1=fft(imp);

R2=phase(imp);

subplot(2,1,1),area(t,abs(R1));

title("Амплитудный спектр прямоугольного сигнала");

Xlabel("Частота");

ylabel("Модуль Фурье-образа сигнала");

grid on;

subplot(2,1,2),plot(t,R2);

title("Фазовый спектр прямоугольного сигнала");

Xlabel("Частота");

ylabel("Фаза");

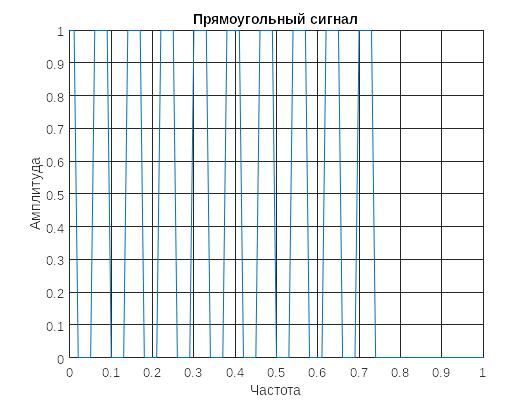
Рисунок 11- прямоугольный сигнал

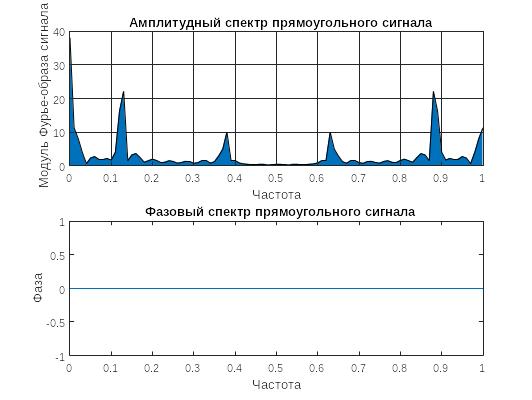
Рисунок 12- спектр прямоугольного сигнала

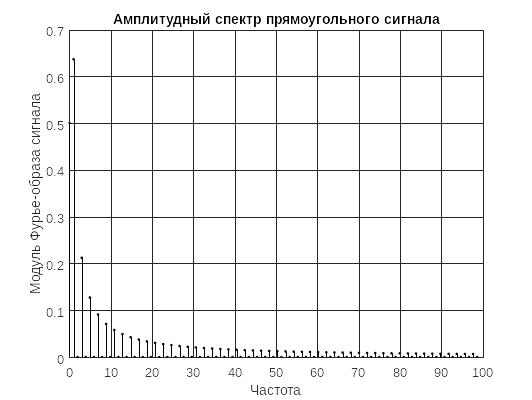
Рисунок 13- спектр прямоугольного сигнала, построенный вручную

6. Создадим базис Уолша для . Построим спектр Фурье этого сигнала (рис. 11) и спектр Уолша (рис. 12).

A = [1 1;1 -1];

B = kron(A,A);

C = kron(B,B);

D = kron(C,B);

E = kron(D,A);

R1=fwht(imp);

walshSpectr= fwht(imp);

FurieSpectr=abs(fft(imp));

walshSpectr=walshSpectr(:,1:101);

subplot(2,1,2),area(t,FurieSpectr),grid on;

title("FurieSpectr");

subplot(2,1,1),area(t,walshSpectr), grid on;

title("WalshSpectr");

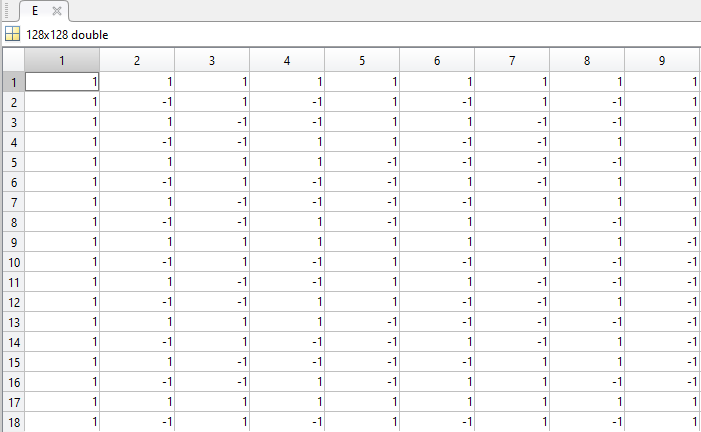
Рисунок 14- матрица Уолша

Рисунок 15- спектр Уолша и Фурье прямоугольного сигнала

7. Определим форму и ширину частотной характеристики двух соседних каналов анализатора Фурье (рис.16). Построим спектр, используя окно Хеннинга (рис. 17).

fs = 1024;

t=0:1/fs:1-1/fs;

for i = 1:100

signal = cos(2*pi*(10+i/10)*t);

sigHann = signal.*hann(1024)';

[ch1(i),ch2(i),ch3(i)]=freqchr(signal);

[chHann1(i),chHann2(i),chHann3(i)]=freqchr(sigHann);

end

figure

hold on

plot(ch1,'k')

plot(ch2,'r')

title('Частотная характеристика 2-х соседних каналов');