МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №2

по дисциплине «Математические основы теории систем»

Тема: Корреляционный метод измерения задержки сигнала

Студентка гр. 9391		Мысик А.С.
Студентка гр. 9391		. Сингх Н.Д
Студент гр. 9391		Фазекаш В.В.
Преподаватель		Гульванский В.В.

Санкт-Петербург

2021

Цель: анализ возможностей корреляционных методов выделения сигнала из шума и измерения его параметров.

Ход работы:

1. Построим излучаемый и принятый импульсы из длинной нулевой последовательности.

X=zeros(1,1000);

Y=zeros(1,1000);

X(1:100)=5;

Y(301:400)=1;

Посчитаем R_xx(τ) – автокорреляционную функцию и построим ее график (рис.1).

conv_R=conv(X,Y);

plot(conv_R);

title('Автокорреляция одного импульса');

xlabel('Время t');

ylabel('Значение');

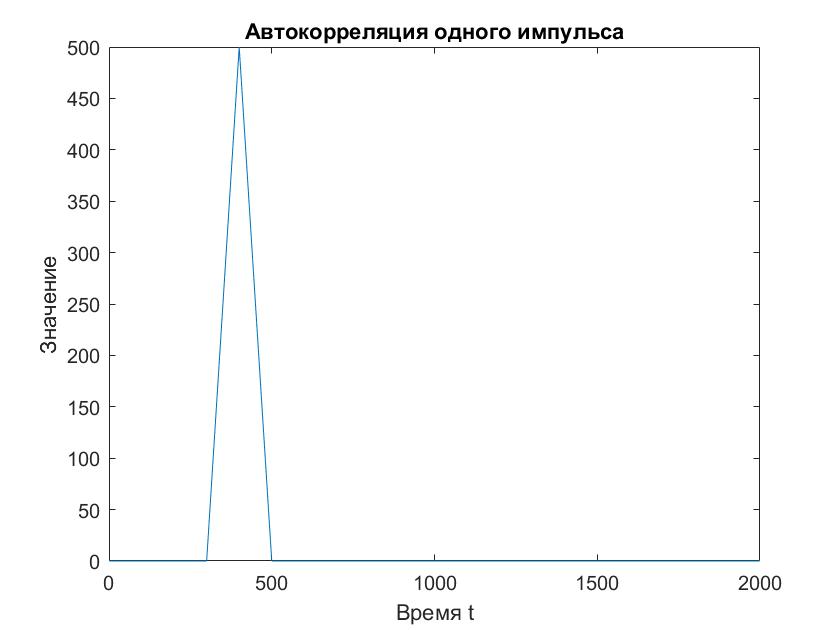
Рисунок 1 - Автокорреляция одного импульса

Добавим еще один отправленный и принятый импульс.

X(300:400)=5;

Y(601:700)=1;

Посчитаем новую R_xx(τ) –корреляционную функцию и построим ее график (рис. 2).

xcorr_R = xcorr(X);

figure;

plot(xcorr_R);

title('Корреляция двух импульсов');

Xlabel('Время t');

ylabel('Значение');

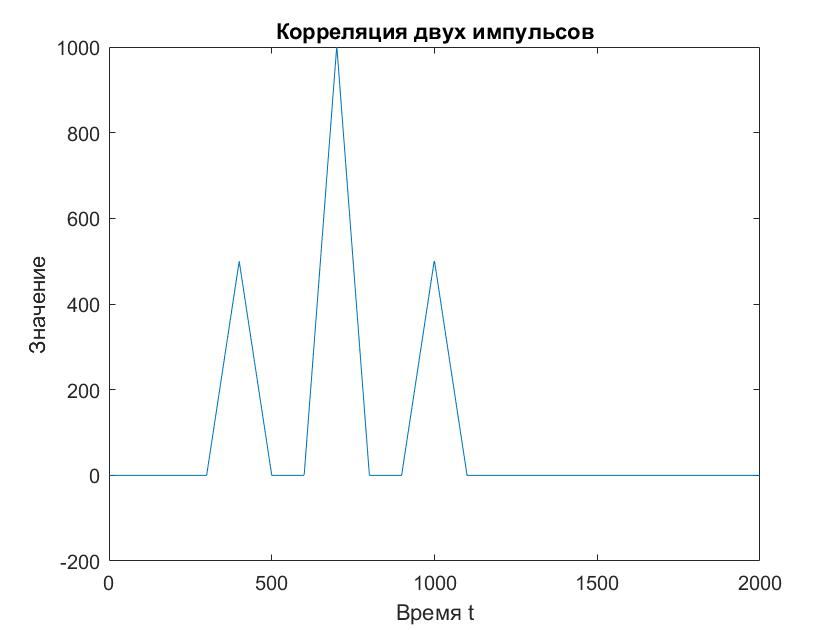
Рисунок 2 - Корреляция двух импульсов

Первый лепесток – автокорреляция первого импульса, приходящаяся на t= 350, где первый отправленный и принятый сигналы совпадают.

Пик – корреляция первого и второго сигнала, приходящаяся на t=650.

Второй лепесток – автокорреляция второго импульса, приходящаяся на t= 1000, где второй отправленный и принятый сигналы совпадают.

2. Создадим еще более сложный сигнал, в котором нет периодических

повторов импульсов и построим его график (рис. 3).

t = 0 : 0.1 : 100;

shift=3;

pulse=0;

for i=1:10

pulse=pulse+rectpuls(t-shift,3);

shift=shift+3+10*rand;

end

figure;

plot(t,pulse),grid, set(gca,'FontSize',12);

title('Сигнал без периодичных повторов импульсов');

Xlabel('Время t');

ylabel('U');

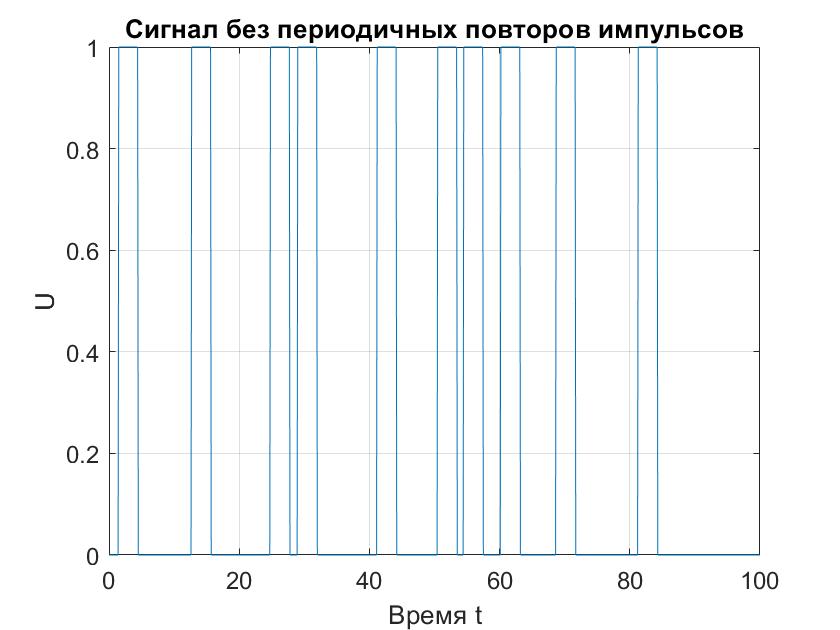
Рисунок 3 - Сигнал без периодичных повторов импульсов

Сымитируем задержку распространения сигнала.

delayed_pulse=zeros (1,300);

delayed_pulse=[delayed_pulse,pulse];

Вычислим Rxx(τ) и Cxx(τ) и построим их графики (рис. 4 и 5).

xcorr_R2 = xcorr(pulse,delayed_pulse);

figure;

plot(xcorr_R2);

title('Корреляция');

Xlabel('Время t');

ylabel('Значение');

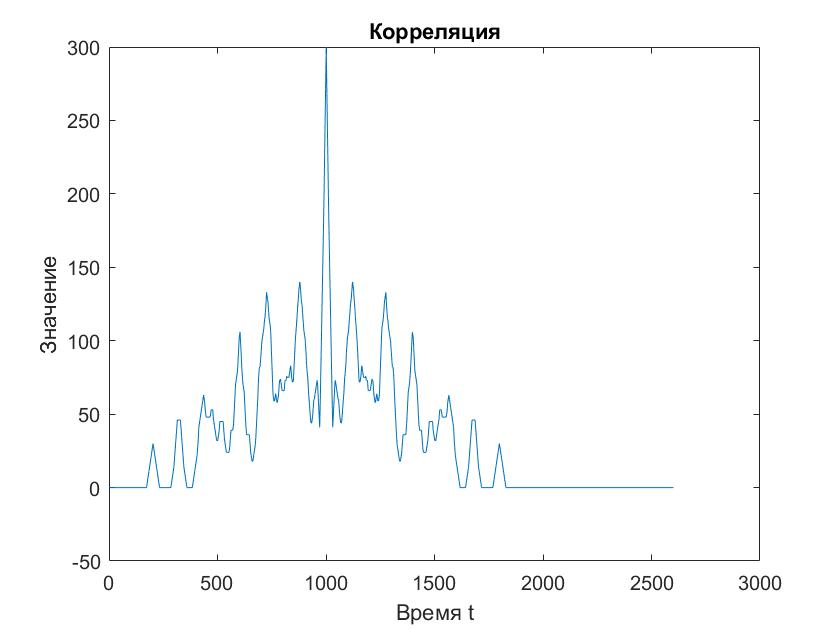
Рисунок 4 - Корреляция

Covariance=xcov(pulse,delayed_pulse);

figure;

plot(Covariance);

title('Ковариация');

Xlabel('Время t');

ylabel('Значение');

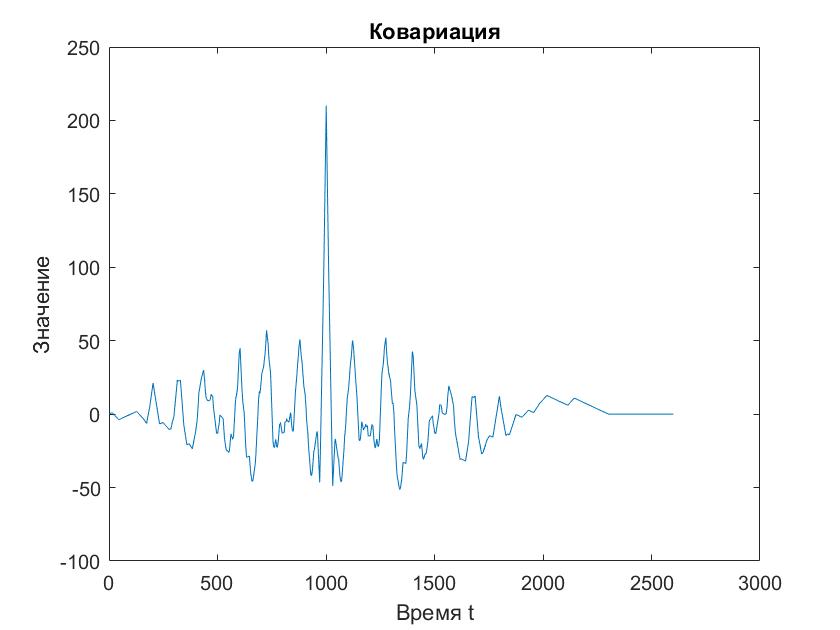
Рисунок 5 - Ковариация

Отличие связано с тем, что корреляция является мерой схожести сигналов, а ковариация из зависимости между собой.

3. Наложим на принятый (задержанный) сигнал шум с соотношением

SNR 3 ÷ 10 дБ и построим график (рис. 6).

figure;

out = awgn(delayed_pulse,0.3);

plot(delayed_pulse);

hold on;

plot(delayed_pulse+out);

legend('Sine Wave','Sine Wave with Noise');

title('Сигнал без периодичных повторов импульсов c шумом');

Xlabel('Время t');

ylabel('U');

hold off;

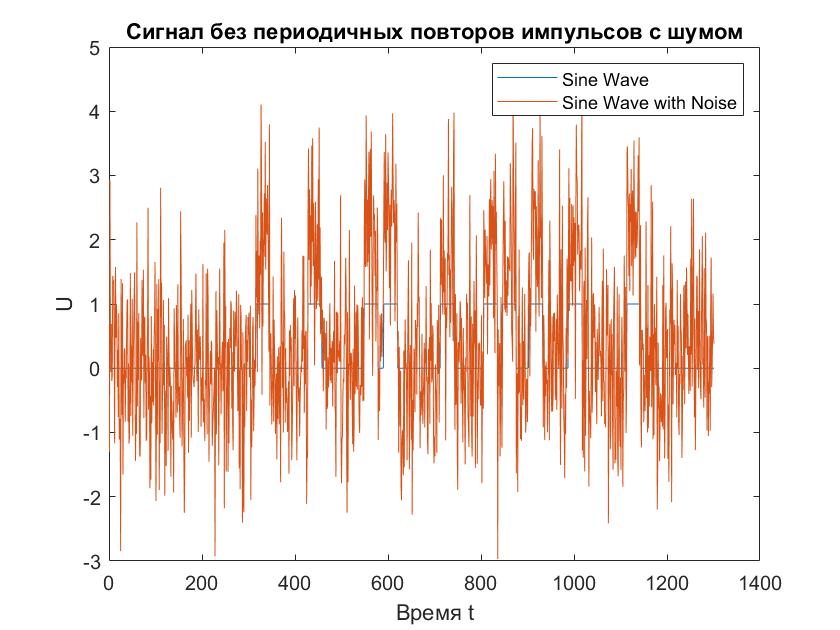
Рисунок 6 - Сигнал без периодических повторов импульсов с шумом

Опытным путем выяснилось, что минимальное значение при котором еще возможно измерение задержки, равно 1.5.

4. В качестве посылаемого сигнала возьмем отрезок синусоиды.

f = 2;

t = 1:0.01:5;

sin_x = sin(2*pi*f*t);

Наложим шум и построим графики (рис.7).

figure

hold on

plot(t,sin_x);

sin_x_noise = awgn(sin_x,10);

plot(t,(sin_x+sin_x_noise));

legend('Sine Wave','Sine Wave with Noise');

title('Синусоида с шумом');

Xlabel('Время t');

ylabel('U');

hold off;

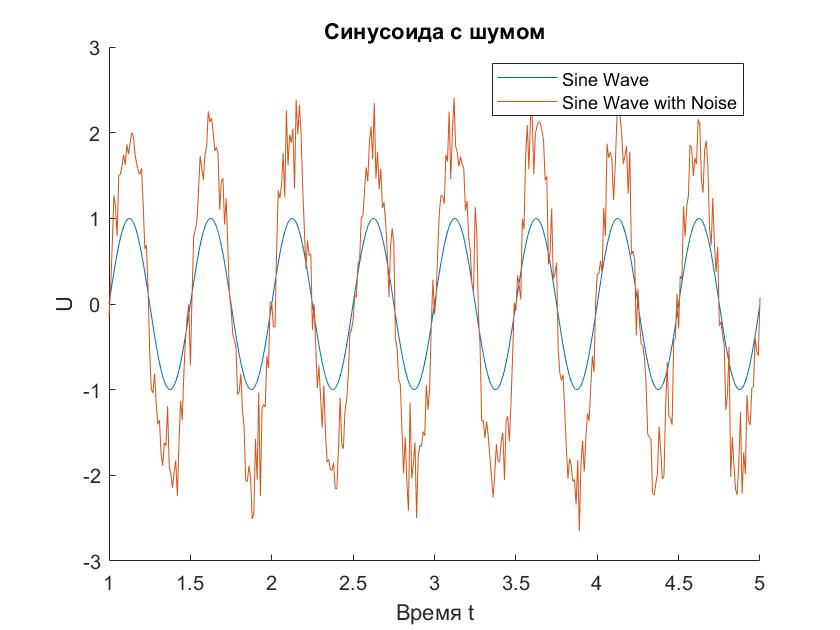
Рисунок 7 - Синусоида и синусоида с шумом

Вычислим Rxx(τ) и построим его график (рис.8).

t=1:0.01:9;

xcorr_R3=xcorr(sin_x,(sin_x+sin_x_noise));

figure

plot(t,xcorr_R3),grid;

title('Корреляция');

Xlabel('Время t');

ylabel('Значение');

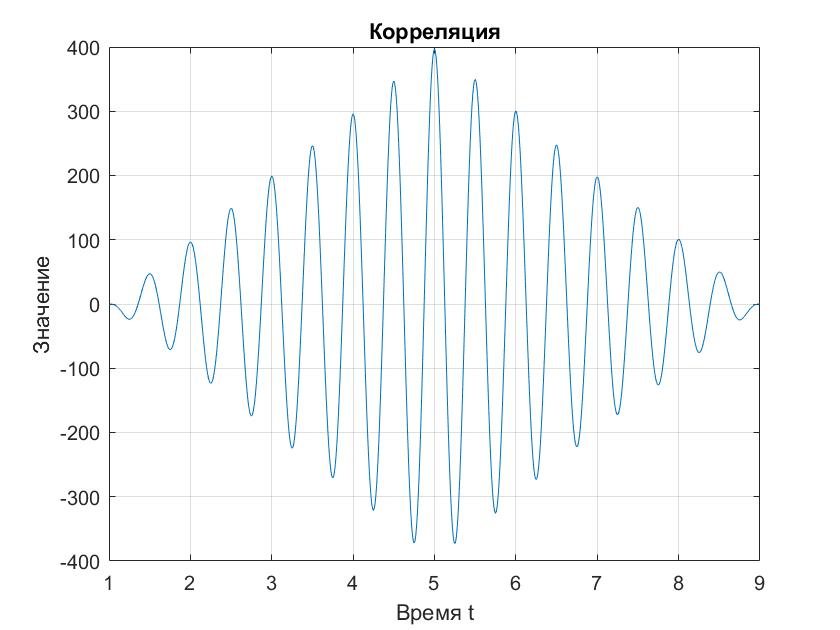
Рисунок 8 - Корреляция

Чтобы найти задержку на функции корреляции необходимо найти t при котором будет наибольшее значение функции корреляции. В данном случае это t=500.

5. Построим сигнал с помощью кода Баркера и наложим на него шум. Построим график (рис. 9).

barker = comm.BarkerCode('Length',11,'SamplesPerFrame',11);

Bar = barker();

Bar = Bar';

t = 0:(length(Bar)*11) - 1;

s0 = square(t);

s(1:121)=0;

for j=1:11

for i=1:11

s(:,i*j) = s0(:,i*j)*Bar(j);

end

end

figure

hold on

plot(t, s,'r');

w_noise = awgn(s,10);

plot(t,w_noise,'y');

legend('Sine Wave','Sine Wave with Noise');

title('Промодулировали несущую кодом Баркера');