
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
отчет
по лабораторной работе №3
по дисциплине «Организация ЭВМ и систем»
Тема: «ИССЛЕДОВАНИЕ ВИДЕОСИСТЕМЫ
(ГРАФИЧЕСКИЙ РЕЖИМ)»
Вариант - 12
Студент гр. 1391 |
|
Поникаровский А. В. |
Преподаватель |
|
Анисимов А. В. |
Санкт-Петербург
2022
Цель работы
Изучение работы с видеосистемой в графическом режиме, вывод
графика заданной функции с масштабированием и разметкой осей.
Основные теоретические положения
Для использования графики в языке С++ прежде всего необходимо определить тип видеоадаптера. Затем устанавливается подходящий режим его работы и выполняется инициализация графической системы в выбранном режиме. После этого становятся доступными для использования функции графической библиотеки graphicx.h для построения основных графических примитивов: отрезков прямых линий, окружностей, эллипсов, прямоугольников, секторов, дуг и т.д., появляется возможность вывода текста с использованием различных шрифтов.
С++ "маскирует" многие технические детали управления оборудованием, о которых пользователь должен быть осведомлён при работе с видеоадаптером через порты или BIOS. Использование графической библиотеки С++ требует знакомства с моделью графической системы, применяемой компилятором для представления графической системы компьютера. Можно сказать, что сложность овладения деталями аппаратных средств видеоадаптеров сравнима со сложностью освоения графической модели. Однако достоинство графической модели заключается в её относительной независимости от различных типов видеоадаптеров и открытости для дальнейших расширений. Появление новых типов видеоадаптеров не потребует большой переработки программ, так как все новые особенности аппаратуры будут учитываться в средствах библиотеки С++.
Весь код библиотеки графики разбивается на две части: немобильную, которая зависит от типа видеоадаптера и мобильную.
Немобильная часть представляет собой так называемый. BGI-драйвер (BGI - Borland Graphics Interface). Драйвер является обработчиком прерывания 10h, который должен дополнить системный обработчик до того, как будут использоваться мобильные функции. Перед завершением программы таблица векторов прерывания восстанавливается.
Основные функции, выполняемые BGI-драйвером, сводятся к установке и обновлению ряда внешних переменных, которые могут изменяться как функциями системного обработчика прерывания 10h (например, при переключении видеорежима, изменении регистров палитры и т.п.), так и мобильными функциями библиотеки графики. С++ включает целую коллекцию драйверов для каждого из типов адаптеров, хранимых обычно в отдельном поддиректории. Система графики является открытой для расширений, так как позволяет использовать и собственные. BGI-драйверы. Сложность состоит в том, что фирма Borland International не раскрывает пока внутреннюю структуру драйвера.
Задание на лабораторную работу
1. Разработать программу для вывода на экран графика заданной функции.
2. Произвести разметку осей и проставить истинные значения точек.
3. Найти максимальное значение функции на заданном интервале и вывести в отдельное окно на экране.
Sin3(x)- Cos2(x) |
π/2 |
8π |
Код программы
#include <graphics.h>
#include <stdio.h>
#include <math.h>
#include <conio.h>
const int xStart = 10;
const float start = 3.14 / 2;
const float end = 3.14 * 8;
const int numberOfSteps = 200;
struct point {
int X;
int Y;
};
point getCoords(float x, float y, float xValue, float yValue){
int maxY = getmaxy();
int avrgY = maxY / 2;
point result;
int currX = xStart;
float realValue = 0;
if (x < 0)
for (; realValue > x; realValue -= xValue, --currX);
else
for (; realValue < x; realValue += xValue, ++currX);
result.X = currX;
realValue = 0;
int currY = avrgY;
if (y < 0)
for (; realValue > y; realValue -= yValue, ++currY);
else
for (; realValue < y; realValue += yValue, --currY);
result.Y = currY;
return result;
}
float max(float* arr, int size) {
float result = arr[0];
for (int i = 1; i < size; ++i) {
if (arr[i] > result)
result = arr[i];
}
return result;
}
float min(float* arr, int size) {
float result = arr[0];
for (int i = 0; i < size; ++i)
if (arr[i] < result)
result = arr[i];
return result;
}
float myFunction(float x) {
return pow(sin(x), 3) - pow(cos(x), 2);
}
void putAxis(float xValue, float yValue) {
int maxX = getmaxx();
int maxY = getmaxy();
int avrgY = maxY / 2;
line(0, avrgY, maxX, avrgY);
line(xStart, 0, xStart, maxY);
for (int i = 1; i < 9; ++i)
{
point p1 = getCoords(3.14 * i, 0, xValue, yValue);
line(p1.X, p1.Y - 5, p1.X, p1.Y + 5);
char c[] = { i + '0', 'p', 'i', '\0' };
outtextxy(p1.X - 10, p1.Y + 20, c);
}
for (int j = 1; j <= 15; j += 2)
{
point p = getCoords(3.15 * j / 2, 0, xValue, yValue);
line(p.X, p.Y - 5, p.X, p.Y + 5);
char c[] = " pi/2";
c[1] = j % 10 + '0';
if (j >= 10)
c[0] = j / 10 + '0';
outtextxy(p.X - 15, p.Y + 15, c);
}
for (int k = 1; k < 10; ++k)
{
point p1 = getCoords(0, float(k) / 10, xValue, yValue);
point p2 = getCoords(0, -float(k) / 10, xValue, yValue);
line(p1.X - 5, p1.Y, p1.X + 5, p1.Y);
line(p2.X - 5, p2.Y, p2.X + 5, p2.Y);
char c1[] = "0. ";
char c2[] = "-0. ";
c1[2] = c2[3] = k + '0';
outtextxy(p1.X + 10, p1.Y, c1);
outtextxy(p2.X + 10, p2.Y, c2);
}
}
void drawGraph(float* X, float* Y, float xValue, float yValue) {
for (int i = 0; i < numberOfSteps - 1; ++i)
{
point p1 = getCoords(X[i], Y[i], xValue, yValue);
point p2 = getCoords(X[i + 1], Y[i + 1], xValue, yValue);
line(p1.X, p1.Y, p2.X, p2.Y);
}
point p = getCoords(3.14 / 2, 0.5, xValue, yValue);
}
int main(){
clrscr();
int grMode, grDriver;
grDriver = DETECT;
grMode = 0;
initgraph(&grDriver, &grMode, "C:\\TurboC3\\BGI");
float* X = new float[numberOfSteps];
float step = (end - start) / numberOfSteps;
float* Y = new float[numberOfSteps];
X[0] = 3.14 / 2;
Y[0] = myFunction(3.14 / 2);
for (int i = 1; i < numberOfSteps; ++i) {
X[i] = X[i - 1] + step;
Y[i] = myFunction(X[i]);
}
float xValue = end / getmaxx();
float yValue = (max(Y, numberOfSteps) - min(Y, numberOfSteps)) / getmaxy();
putAxis(xValue, yValue);
drawGraph(X, Y, xValue, yValue);
getch();
delete[] X;
delete[] Y;
closegraph();
return 0;
}
Работа программы
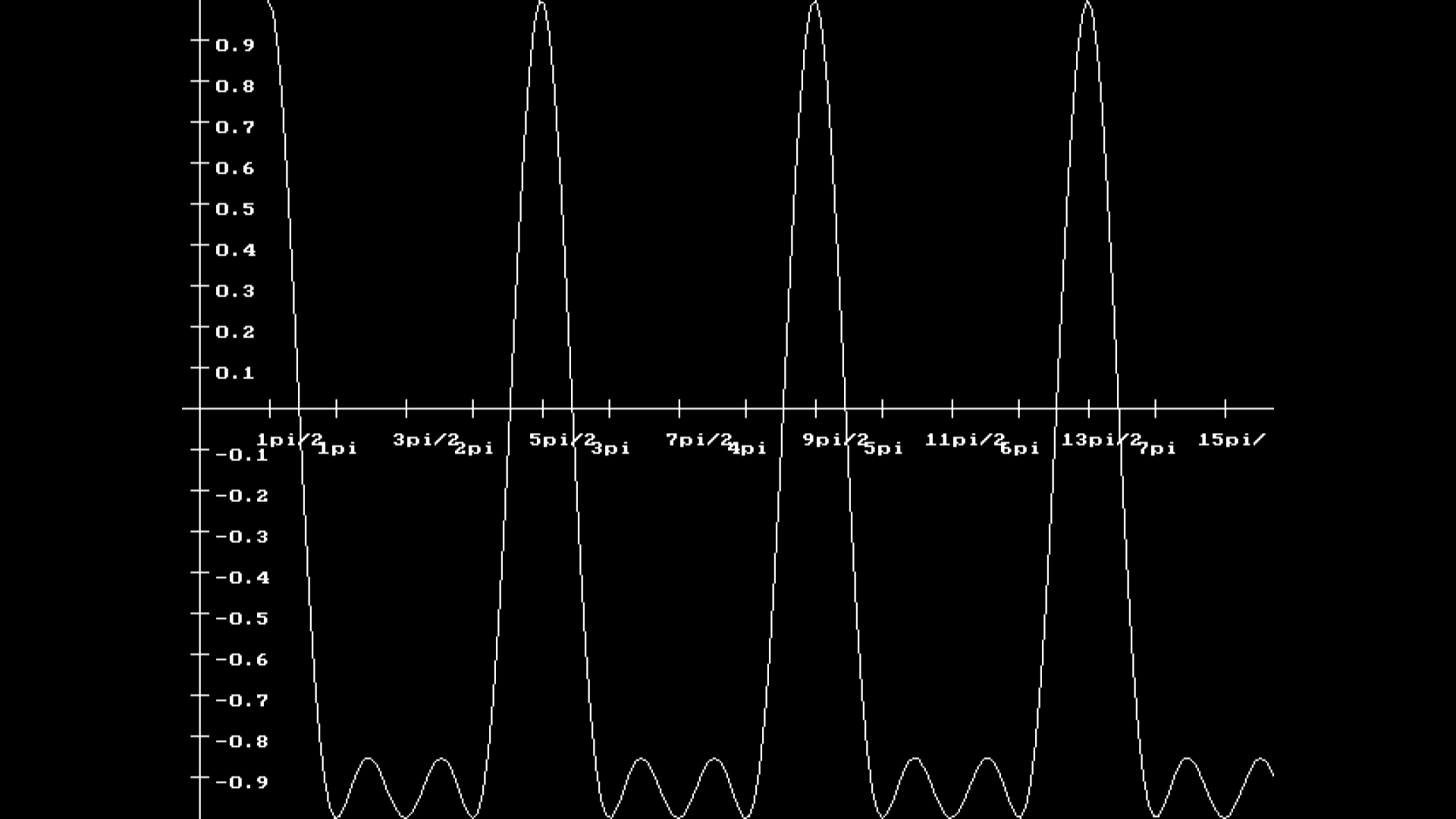
Выводы
Изучена работа с видеосистемой в графическом режиме, вывод графика заданной функции с масштабированием и разметкой осей.
