ЛР7, В15

import numpy as np import sympy as sp from sympy import * import matplotlib.pyplot as plt from scipy.optimize import root_scalar import math from scipy.integrate import quad from scipy.optimize import minimize_scalar from sympy import Matrix from scipy.integrate import solve_ivp

1.1

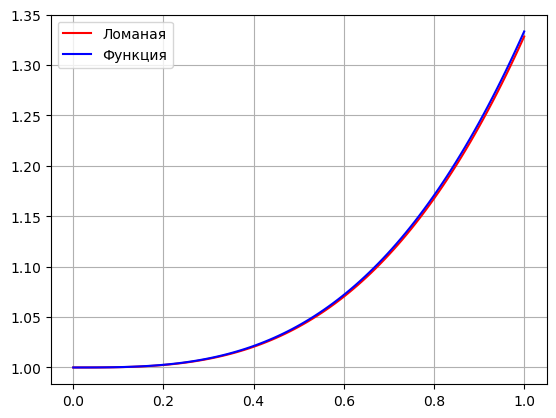
def eiler(f, x0, y0, h, N): xi = [x0] yi = [y0] for i in range(N): fi = f.subs(x, xi[i]).subs(y, yi[i]) xi.append(xi[i] + h) yi.append(yi[i] + h * fi) return xi, yi x, y = sp.symbols('x y') dxdy = x**2 x0 = 0 y0 = 1 a = x0 b = 1 h = 0.01 N = int((b - a) / h) xi, yi = eiler(dxdy, x0, y0, h, N) plt.plot(xi, yi, 'r', label = 'Ломаная') xx = np.linspace(a, b, 100) f = xx**3/3 + 1 plt.plot(xx, f, 'b', label = 'Функция') ff = x**3/3 + 1 print(f'Разница: {np.abs(yi[-1] - ff.subs(x, b))}') plt.legend() plt.grid() plt.show()

Разница: 0.00498333333333378

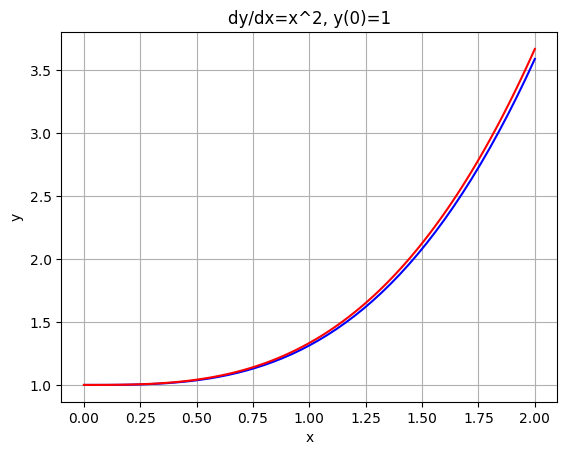
import numpy as np import matplotlib.pyplot as plt import sympy as sp def Eiler(f, x0, y0, b, n): h = (b - x0) / n xi = [x0] yi = [y0] for i in range(n): fi = f.subs(x, xi[i]).subs(y, yi[i]) xi.append(xi[i] + h) yi.append(yi[i] + h * fi) u = yi[-1] du = plt.plot(xi, yi, 'b') plt.xlabel('x') plt.ylabel('y') return u # Пример использования x, y = sp.symbols('x y') f = x**2 x0 = 0 y0 = 1 X = 2 n = 50 u = Eiler(f, x0, y0, X, n) plt.plot(np.linspace(0, X, 100), [v**3/3 + 1 for v in np.linspace(0, X, 100)], 'r') plt.title('dy/dx=x^2, y(0)=1') dy = abs(u - (X**3/3 + 1)) print(f'Абсолютная разница между численным и аналитическим решениями: {dy}') plt.grid() plt.show()

Абсолютная разница между численным и аналитическим решениями: 0.0794666666666646

2.1

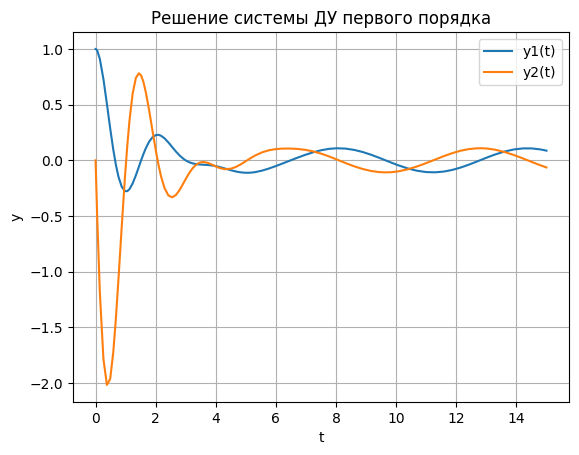
def system(t, y): y1, y2 = y dydt1 = y2 dydt2 = -2 * y2 - 10 * y1 + np.sin(t) return [dydt1, dydt2] t_span = [0, 15] y0 = [1, 0] sol = solve_ivp(system, t_span, y0, method='RK23') t = sol.t y1 = sol.y[0] y2 = sol.y[1] plt.plot(t, y1, label='y1(t)') plt.plot(t, y2, label='y2(t)') plt.xlabel('t') plt.ylabel('y') plt.title('Решение системы ДУ первого порядка') plt.legend() plt.grid() plt.show()

def system(t, y): y1, y2 = y dydt1 = y2 dydt2 = -2 * y2 - 10 * y1 + np.sin(t) return [dydt1, dydt2] t_span = [0, 15] y0 = [1, 0] sol = solve_ivp(system, t_span, y0, method='RK45') t = sol.t y1 = sol.y[0] y2 = sol.y[1] plt.plot(t, y1, label='y1(t)') plt.plot(t, y2, label='y2(t)') plt.xlabel('t') plt.ylabel('y') plt.title('Решение системы ДУ первого порядка') plt.legend() plt.grid() plt.show()

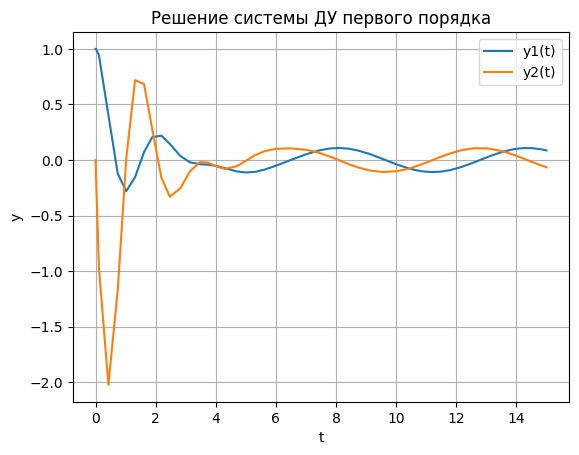
2.2

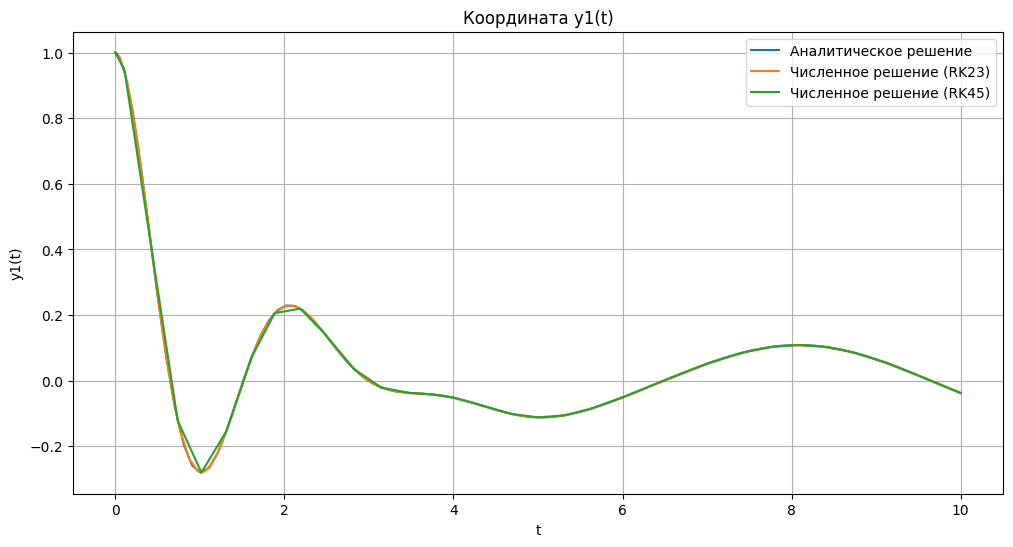
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp # Аналитическое решение def analytical_solution(t): C1 = 87/85 C2 = 26/85 return np.exp(-t) * (C1 * np.cos(3*t) + C2 * np.sin(3*t)) + (1/85) * (9 * np.sin(t) - 2 * np.cos(t)) # Система дифференциальных уравнений def system(t, y): y1, y2 = y dydt1 = y2 dydt2 = -2 * y2 - 10 * y1 + np.sin(t) return [dydt1, dydt2] # Начальные условия y0 = [1, 0] t_span = [0, 10] # Численное решение с помощью RK23 и RK45 sol_rk23 = solve_ivp(system, t_span, y0, method='RK23') sol_rk45 = solve_ivp(system, t_span, y0, method='RK45') # Построение графиков t = np.linspace(0, 10, 100) y1_analytical = analytical_solution(t) y1_rk23 = sol_rk23.y[0] y1_rk45 = sol_rk45.y[0] y2_rk23 = sol_rk23.y[1] y2_rk45 = sol_rk45.y[1] plt.figure(figsize=(12, 6)) plt.plot(t, y1_analytical, label='Аналитическое решение') plt.plot(sol_rk23.t, y1_rk23, label='Численное решение (RK23)') plt.plot(sol_rk45.t, y1_rk45, label='Численное решение (RK45)') plt.xlabel('t') plt.ylabel('y1(t)') plt.title('Координата y1(t)') plt.legend() plt.grid() plt.show()

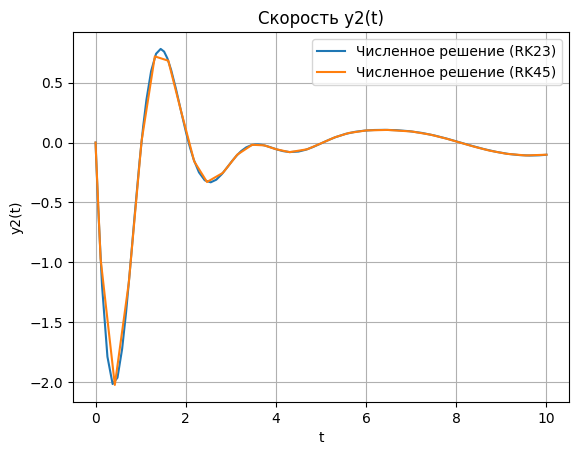
plt.plot(sol_rk23.t, y2_rk23, label='Численное решение (RK23)') plt.plot(sol_rk45.t, y2_rk45, label='Численное решение (RK45)') plt.xlabel('t') plt.ylabel('y2(t)') plt.title('Скорость y2(t)') plt.legend() plt.grid() plt.show()

3.1

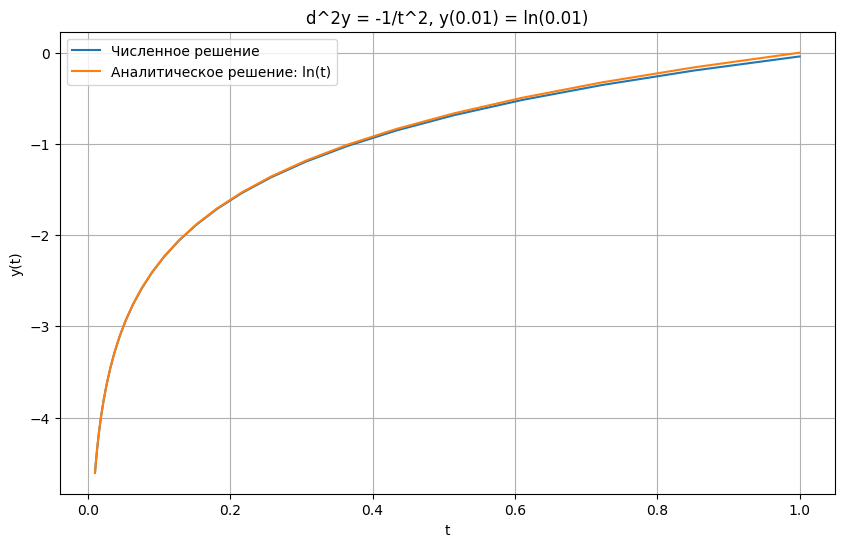
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp def solver_(t, Y0): dydt = [Y0[1], -1/t**2] return dydt Y0 = [np.log(0.01), 1/0.01] t_span = [0.01, 1] t_eval = np.linspace(0.01, 1, 100) #sol = solve_ivp(solver_, t_span, Y0, t_eval=t_eval) sol = solve_ivp(solver_, t_span, Y0, method='RK23') t = sol.t y = sol.y[0] # Построение графиков plt.figure(figsize=(10, 6)) # График численного решения plt.plot(t, y, label='Численное решение') # График аналитического решения plt.plot(t, np.log(t), label='Аналитическое решение: ln(t)') plt.xlabel('t') plt.ylabel('y(t)') plt.title('d^2y = -1/t^2, y(0.01) = ln(0.01)') plt.legend() plt.grid() plt.show()