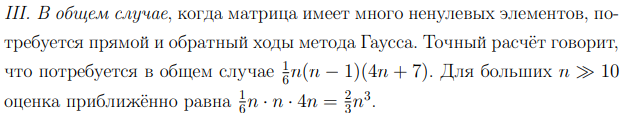ЛР / Лаб. 6 ЧМ
.docxЛР6, В15
import numpy as np import sympy as sp from sympy import * import matplotlib.pyplot as plt from scipy.optimize import root_scalar import math from scipy.integrate import quad from scipy.optimize import minimize_scalar from sympy import Matrix
3.1

def inverse_matrix(A, f): X_inv = np.dot(np.linalg.inv(A), f) print("Решение с помощью обратной матрицы:") print(X_inv, "\n") def kramer(A, f): X_kramer = np.empty_like(f) for i in range(len(f)): A_i = A.copy() A_i[:, i] = f.flatten() X_kramer[i] = np.linalg.det(A_i) / det_A print("Решение с помощью правила Крамера:") print(X_kramer, "\n") A = np.random.uniform(0, 10, (3, 3)) f = np.random.uniform(0, 10, (3, 1)) #A = np.array([[2, 1, -1], # [-3, -1, 2], # [-2, 1, 2]], dtype=float) #f = np.array([8, -11, -3], dtype=float) det_A = np.linalg.det(A) if det_A != 0: inverse_matrix(A, f) kramer(A, f) else: print("Матрица A вырожденная, решение невозможно.")
Решение с помощью обратной матрицы: [[-0.66999811] [ 0.60582837] [ 1.1211053 ]] Решение с помощью правила Крамера: [[-0.66999811] [ 0.60582837] [ 1.1211053 ]]
3.2
![]()
def find_max_ind(matrix, col): i = np.argmax(np.abs(matrix[col:, col])) + col return i def swap_rows(matrix, row1, row2): matrix[[row1, row2]] = matrix[[row2, row1]] def gauss(A, f): n = len(f) for i in range(n): #print(f'i: {i}') i_max = find_max_ind(A, i) #print(f'pivot_row: {pivot_row}') swap_rows(A, i, i_max) swap_rows(f, i, i_max) #print(f'A:\n{A}') #print(f'f:\n{f}') Aii = A[i, i] #print(f'pivot_val: {pivot_val}') A[i] = A[i] / Aii f[i] = f[i] / Aii #print(f'A:\n{A}') #print(f'f:\n{f}') for j in range(i+1, n): #print(f'j: {j}') factor = A[j, i] #print(f'factor: {factor}') A[j] -= factor * A[i] f[j] -= factor * f[i] #print(f'A:\n{A}') #print(f'f:\n{f}\n') x = np.zeros(n) for i in range(n-1, -1, -1): x[i] = (f[i] - np.dot(A[i, i+1:], x[i+1:])) / A[i, i] return x A = np.array([[2, 1, -1], [-3, -1, 2], [-2, 1, 2]], dtype=float) f = np.array([8, -11, -3], dtype=float) A = np.random.uniform(0, 10, (3, 3)) f = np.random.uniform(0, 10, (3, 1)) solution = gauss(A, f) print("Решение системы уравнений:", solution)
<ipython-input-111-e495b84ea66e>:34: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.) x[i] = (f[i] - np.dot(A[i, i+1:], x[i+1:])) / A[i, i]
Решение системы уравнений: [ 0.44941841 0.41800046 -0.03694168]
...
def find_max_ind(matrix, col): i = np.argmax(np.abs(matrix[col:, col])) + col return i def swap_rows(matrix, row1, row2): matrix[[row1, row2]] = matrix[[row2, row1]] def gauss(A, f): n = len(f) for i in range(n): #print(f'i: {i}') i_max = find_max_ind(A, i) #print(f'pivot_row: {pivot_row}') swap_rows(A, i, i_max) swap_rows(f, i, i_max) #print(f'A:\n{A}') #print(f'f:\n{f}') for j in range(i+1, n): #print(f'j: {j}') k = A[j, i] / A[i, i] #print(f'factor: {factor}') f[j] -= k * f[i] A[j, i:] -= k * A[i, i:] #print(f'A:\n{A}') #print(f'f:\n{f}\n') x = np.zeros(n) for i in range(n-1, -1, -1): #print(f'i: {i}') x[i] = (f[i] - np.dot(A[i,i+1:], x[i+1:])) / A[i,i] #print(f'x[i]: {x[i]}') return x A = np.array([[2, 1, -1], [-3, -1, 2], [-2, 1, 2]], dtype=float) f = np.array([8, -11, -3], dtype=float) A = np.random.uniform(0, 10, (3, 3)) f = np.random.uniform(0, 10, (3, 1)) solution = gauss(A, f) print("Решение системы уравнений:", solution) def gauss2(A, f): n = len(f) for i in range(n): #print(f'i: {i}') #i_max = find_max_ind(A, i) #print(f'pivot_row: {pivot_row}') #swap_rows(A, i, i_max) #swap_rows(f, i, i_max) #print(f'A:\n{A}') #print(f'f:\n{f}') for j in range(i+1, n): #print(f'j: {j}') k = A[j, i] / A[i, i] #print(f'factor: {factor}') f[j] -= k * f[i] A[j, i:] -= k * A[i, i:] #print(f'A:\n{A}') #print(f'f:\n{f}\n') x = np.zeros(n) for i in range(n-1, -1, -1): #print(f'i: {i}') x[i] = (f[i] - np.dot(A[i,i+1:], x[i+1:])) / A[i,i] #print(f'x[i]: {x[i]}') return x #solution = gauss2(A, f) #print("Решение системы уравнений:", solution)
3.3

# A = np.random.uniform(0, 10, (3, 3)) # f = np.random.uniform(0, 10, (3, 1)) # A = Matrix(A) # f = Matrix(f) A = Matrix([[2, 1, -1], [-3, -1, 2], [-2, 1, 2]]) f = Matrix([8, -11, -3]) M = A.row_join(f) M_rref, pivot_columns = M.rref() solution = M_rref[:, -1] solution = np.array(solution) solution = solution.flatten() print("Решение системы уравнений:", solution)
Решение системы уравнений: [2 3 -1]
A = np.array([[2, 1, -1], [-3, -1, 2], [-2, 1, 2]], dtype=float) f = np.array([8, -11, -3], dtype=float) #solution = np.linalg.solve(A, f) x,resid,rank,s = np.linalg.lstsq(A, f, rcond=None) print("Решение системы уравнений:", x)
Решение системы уравнений: [ 2. 3. -1.]
3.4

n = 20 A = np.random.rand(n, n) X = np.random.rand(n) cond_A = np.linalg.cond(A) print("Число обусловленности матрицы A до изменений:", cond_A) if cond_A < 10**3: A[n-1, n-1] = 1000 cond_A = np.linalg.cond(A) print("Число обусловленности матрицы A после изменений:", cond_A, "\n") f = np.dot(A, X) det_A = np.linalg.det(A) if det_A != 0: inverse_matrix(A, f) kramer(A, f) else: print("Матрица A вырожденная, решение невозможно.") #--------------------------------------- solution = gauss2(A, f) print("Решение системы уравнений обычным методом Гаусса:\n", solution, "\n") #--------------------------------------- solution = gauss(A, f) print("Решение системы уравнений методом Гаусса с выбором главного элемента:\n", solution, "\n") #--------------------------------------- x,resid,rank,s = np.linalg.lstsq(A, f, rcond=None) print("Решение системы уравнений A \ f:\n", x, "\n") #--------------------------------------- A = Matrix(A) f = Matrix(f) M = A.row_join(f) M_rref, pivot_columns = M.rref() solution = M_rref[:, -1] solution = np.array(solution) solution = solution.flatten() print("Решение системы уравнений функцией rref:\n", solution)
Число обусловленности матрицы A до изменений: 124.32429305744304 Число обусловленности матрицы A после изменений: 30357.179705957136 Решение с помощью обратной матрицы: [0.73824087 0.27038915 0.98733201 0.8358836 0.89035239 0.54898351 0.29894813 0.94427285 0.24550163 0.32668989 0.75799096 0.31297487 0.76424858 0.9878296 0.11883112 0.26031062 0.41126332 0.39404393 0.62199281 0.78547556] Решение с помощью правила Крамера: [0.73824087 0.27038915 0.98733201 0.8358836 0.89035239 0.54898351 0.29894813 0.94427285 0.24550163 0.32668989 0.75799096 0.31297487 0.76424858 0.9878296 0.11883112 0.26031062 0.41126332 0.39404393 0.62199281 0.78547556] Решение системы уравнений обычным методом Гаусса: [0.73824087 0.27038915 0.98733201 0.8358836 0.89035239 0.54898351 0.29894813 0.94427285 0.24550163 0.32668989 0.75799096 0.31297487 0.76424858 0.9878296 0.11883112 0.26031062 0.41126332 0.39404393 0.62199281 0.78547556] Решение системы уравнений методом Гаусса с выбором главного элемента: [0.73824087 0.27038915 0.98733201 0.8358836 0.89035239 0.54898351 0.29894813 0.94427285 0.24550163 0.32668989 0.75799096 0.31297487 0.76424858 0.9878296 0.11883112 0.26031062 0.41126332 0.39404393 0.62199281 0.78547556] Решение системы уравнений A \ f: [0.73824087 0.27038915 0.98733201 0.8358836 0.89035239 0.54898351 0.29894813 0.94427285 0.24550163 0.32668989 0.75799096 0.31297487 0.76424858 0.9878296 0.11883112 0.26031062 0.41126332 0.39404393 0.62199281 0.78547556] Решение системы уравнений функцией rref: [0.738240870603048 0.270389145616749 0.987332008345409 0.835883603960227 0.890352392331237 0.548983509453502 0.298948128586497 0.944272852051743 0.245501629156276 0.326689887474658 0.757990962747018 0.312974865945531 0.764248584209720 0.987829601603827 0.118831121260363 0.260310620021524 0.411263324615403 0.394043934951893 0.621992807860390 0.785475558142453]
Сравнить количество арифм операций м.Гаусса и итер. методов