ЛР / Лаб. 5 ЧМ

ЛР5, В15

import numpy as np import sympy as sp from sympy import * import matplotlib.pyplot as plt from scipy.optimize import root_scalar import math from scipy.integrate import quad from scipy.optimize import minimize_scalar

1.1

def f(x): return x**3 #return x**2 #return x/2 def Mi(ff, x, a, b, i): der = sp.diff(ff, x, i) points = np.linspace(a, b) points.tolist() der_list = [der.subs(x, point) for point in points] Mi = max(der_list) #print(M2) return Mi def trapezoid(xx, f, res, Mi): i = 0 #for j in range(len(xx) - 1): #i += (f(xx[j])+f(xx[j+1]))*((xx[j+1]-xx[j])/2) for j in range(1, len(xx) - 1): i += f(xx[j]) i += (f(xx[0]) + f(xx[len(xx) - 1]))/2 h = xx[1]-xx[0] i = i*h print(f'Шаг: {h}') print(f'Значение: {i}') print(f'Погрешность экспериментальная: {np.abs(i - result)}') #M2 = derivate(ff, x, a, b) print(f'Погрешность теоретическая: {(h**2*(b-a)*Mi)/12}\n') #return i x = sp.symbols('x') a = 0 b = 1 x_ = np.linspace(a, b) ff = x**3 result, error = quad(f, a, b) print(f'Значение интеграла: {result}\n') # print(error) #M2 = derivate(ff, x, a, b) #print(M2) #xx = [] for i in range(10, 101, 10): xx = np.linspace(a, b, i) xx.tolist() trapezoid(xx, f, result, Mi(ff, x, a, b, 2)) print(f'Максимальная погрешность:') xx = np.linspace(a, b, 2) xx.tolist() trapezoid(xx, f, result, Mi(ff, x, a, b, 2)) #xx = np.linspace(0, 1, 10) #xx.tolist() #print(trapezoid2(xx, f)) #plt.plot(x_, f(x_)) #plt.grid() #plt.show()

Значение интеграла: 0.25 Шаг: 0.1111111111111111 Значение: 0.2530864197530864 Погрешность экспериментальная: 0.003086419753086378 Погрешность теоретическая: 0.00617283950617284 Шаг: 0.05263157894736842 Значение: 0.2506925207756232 Погрешность экспериментальная: 0.0006925207756232066 Погрешность теоретическая: 0.00138504155124654 Шаг: 0.034482758620689655 Значение: 0.25029726516052314 Погрешность экспериментальная: 0.00029726516052314134 Погрешность теоретическая: 0.000594530321046373 Шаг: 0.02564102564102564 Значение: 0.2501643655489809 Погрешность экспериментальная: 0.00016436554898091593 Погрешность теоретическая: 0.000328731097961867 Шаг: 0.02040816326530612 Значение: 0.25010412328196574 Погрешность экспериментальная: 0.00010412328196574006 Погрешность теоретическая: 0.000208246563931695 Шаг: 0.01694915254237288 Значение: 0.2500718184429762 Погрешность экспериментальная: 7.181844297621254e-05 Погрешность теоретическая: 0.000143636885952313 Шаг: 0.014492753623188406 Значение: 0.2500525099768956 Погрешность экспериментальная: 5.250997689559833e-05 Погрешность теоретическая: 0.000105019953791220 Шаг: 0.012658227848101266 Значение: 0.2500400576830636 Погрешность экспериментальная: 4.005768306358792e-05 Погрешность теоретическая: 0.0000801153661272232 Шаг: 0.011235955056179775 Значение: 0.25003156167150614 Погрешность экспериментальная: 3.156167150614175e-05 Погрешность теоретическая: 0.0000631233430122459 Шаг: 0.010101010101010102 Значение: 0.2500255076012652 Погрешность экспериментальная: 2.5507601265184476e-05 Погрешность теоретическая: 0.0000510152025303541 Максимальная погрешность: Шаг: 1.0 Значение: 0.5 Погрешность экспериментальная: 0.25 Погрешность теоретическая: 0.500000000000000

def f(x): return x**3 #return x**2 #return x/2 def simpson(xx, f, res, Mi): i = 0 #for j in range(len(xx) - 1): #i += (f(xx[j])+4*f((xx[j+1]+xx[j+1])/2)+f(xx[j+1]))*((xx[j+1]-xx[j])/6) for j in range(1, len(xx) - 1): i += f(xx[j]) i = 2*i + f(xx[0]) + f(xx[len(xx) - 1]) for j in range(len(xx) - 1): i += 4*f((xx[j] + xx[j+1])/2) h = xx[1]-xx[0] i = i*(h/6) print(f'Шаг: {h}') print(f'Значение: {i}') print(f'Погрешность экспериментальная: {np.abs(i - result)}') #M2 = derivate(ff, x, a, b) print(f'Погрешность теоретическая: {(h**4*(b-a)*Mi)/2880}\n') #return i result, error = quad(f, a, b) print(f'Значение интеграла: {result}\n') # print(error) x = sp.symbols('x') a = 0 b = 1 x_ = np.linspace(a, b) ff = x**3 for i in range(10, 101, 10): xx = np.linspace(a, b, i) xx.tolist() simpson(xx, f, result, Mi(ff, x, a, b, 4)) #print(f'Максимальная погрешность:') #xx = np.linspace(a, b, 2) #xx.tolist() #simpson(xx, f, result, Mi(ff, x, a, b, 4))

Значение интеграла: 0.25 Шаг: 0.1111111111111111 Значение: 0.24999999999999992 Погрешность экспериментальная: 8.326672684688674e-17 Погрешность теоретическая: 0 Шаг: 0.05263157894736842 Значение: 0.2499999999999999 Погрешность экспериментальная: 1.1102230246251565e-16 Погрешность теоретическая: 0 Шаг: 0.034482758620689655 Значение: 0.25 Погрешность экспериментальная: 0.0 Погрешность теоретическая: 0 Шаг: 0.02564102564102564 Значение: 0.24999999999999994 Погрешность экспериментальная: 5.551115123125783e-17 Погрешность теоретическая: 0 Шаг: 0.02040816326530612 Значение: 0.25 Погрешность экспериментальная: 0.0 Погрешность теоретическая: 0 Шаг: 0.01694915254237288 Значение: 0.25000000000000006 Погрешность экспериментальная: 5.551115123125783e-17 Погрешность теоретическая: 0 Шаг: 0.014492753623188406 Значение: 0.25 Погрешность экспериментальная: 0.0 Погрешность теоретическая: 0 Шаг: 0.012658227848101266 Значение: 0.25000000000000006 Погрешность экспериментальная: 5.551115123125783e-17 Погрешность теоретическая: 0 Шаг: 0.011235955056179775 Значение: 0.24999999999999994 Погрешность экспериментальная: 5.551115123125783e-17 Погрешность теоретическая: 0 Шаг: 0.010101010101010102 Значение: 0.25000000000000017 Погрешность экспериментальная: 1.6653345369377348e-16 Погрешность теоретическая: 0

2.1

def f(x): return 1/(1+x**2) def trapezoid1(xx, f, res, Mi): i = 0 #for j in range(len(xx) - 1): #i += (f(xx[j])+f(xx[j+1]))*((xx[j+1]-xx[j])/2) for j in range(1, len(xx) - 1): i += f(xx[j]) i += (f(xx[0]) + f(xx[len(xx) - 1]))/2 h = xx[1]-xx[0] i = i*h print(f'По формуле трапеций:') print(f'Шаг: {h}') print(f'Значение: {4*i}') print(f'разница с реальным значением: {np.abs(4*i - np.pi)}\n') def simpson1(xx, f, res, Mi): i = 0 #for j in range(len(xx) - 1): # i += (f(xx[j])+4*f((xx[j+1]+xx[j+1])/2)+f(xx[j+1]))*((xx[j+1]-xx[j])/6) #h = xx[1]-xx[0] for j in range(1, len(xx) - 1): i += f(xx[j]) i = 2*i + f(xx[0]) + f(xx[len(xx) - 1]) for j in range(len(xx) - 1): i += 4*f((xx[j] + xx[j+1])/2) h = xx[1]-xx[0] i = i*(h/6) print(f'По формуле Симпсона:') print(f'Шаг: {h}') print(f'Значение: {4*i}') print(f'Разница с реальным значением: {np.abs(4*i - np.pi)}\n') x = sp.symbols('x') a = 0 b = 1 eps = 10**(-6) ff = 1/(1+x**2) M2 = Mi(ff, x, a, b, 2) h2 = sqrt((12*eps)/(M2*(b-a))) #print(f'Посчитанный шаг: {h}') n_points = int((b-a)/h2) + 2 xx = np.linspace(0, 1, n_points) xx.tolist() trapezoid1(xx, f, result, M2) M4 = Mi(ff, x, a, b, 4) h4 = ((2880*eps)/(M4*(b-a)))**(1/4) #print(f'Посчитанный шаг: {h4}') n_points = int((b-a)/h4) + 2 xx = np.linspace(0, 1, n_points) xx.tolist() simpson1(xx, f, result, M4)

По формуле трапеций: Шаг: 0.004878048780487805 Значение: 3.1415886876964767 разница с реальным значением: 3.965893316415503e-06 По формуле Симпсона: Шаг: 0.1 Значение: 3.141592652969785 Разница с реальным значением: 6.200080449048073e-10

3.1

def f(x): return 1/(1+x**2) def simpson3(f, a, b): h = 1 i_h = 0 i_h2 = 1 i_list = [0, 1] count = 2 while np.abs((i_h - i_h2))/15 > 10**(-6): i_h = 0 i_h_1 = 0 i_h_2 = 0 i_h2 = 0 i_list = [0, 1] n_points = int((b-a)/h) + 1 xx = np.linspace(a, b, n_points) xx.tolist() for j in range(1, len(xx) - 1): i_h_1 += f(xx[j]) i_h_1 = 2*i_h_1 + f(xx[0]) + f(xx[len(xx) - 1]) for j in range(len(xx) - 1): i_h_2 += f((xx[j] + xx[j+1])/2) i_h = (h/6)*(i_h_1 + 4*i_h_2) h = h/2 n_points = int((b-a)/h) + 1 xx = np.linspace(a, b, n_points) xx.tolist() #for j in range(1, len(xx) - 1): # i_h2 += f(xx[j]) #i_h2 = 2*i_h2 + f(xx[0]) + f(xx[len(xx) - 1]) for j in range(len(xx) - 1): i_h2 += 4*f((xx[j] + xx[j+1])/2) i_h2 = (h/6)*(i_h_1 + 2*i_h_2 + i_h2) #print(n_points) #h = xx[1]-xx[0] print(f'По формуле Симпсона:') print(f'Шаг: {h}') print(f'Значение: {4*i_h2}') print(f'Разница с реальным значением: {np.abs(4*i_h2 - np.pi)}') print(f'Разница между шагами: {np.abs(4*i_h2 - 4*i_h)}\n') def trapezoid4(f, a, b): h = 1 #i_list = [0, 1] i_h = 0 i_h2 = 1 count = 2 n_points = int((b-a)/h) + 1 xx = np.linspace(a, b, n_points) xx.tolist() while np.abs((i_h - i_h2))/15 > 10**(-6): #i_list = [0, 0] i_h = 0 i_h2 = 0 #for i in range(len(i_list)): #if i!=1: #h=h/2 n_points = int((b-a)/h) + 1 xx = np.linspace(a, b, n_points) xx.tolist() for j in range(1, len(xx) - 1): i_h += f(xx[j]) i_h += (f(xx[0]) + f(xx[len(xx) - 1]))/2 h = xx[1]-xx[0] i_h = i_h*h h = h/2 #n_points = int((b-a)/h) + 1 #xx = np.linspace(a, b, n_points) #xx.tolist() #for j in range(1, len(xx), 2): # i_h2 += f(xx[j]) for j in range(len(xx) - 1): i_h2 += f((xx[j]+xx[j+1])/2) i_h2 = (h/2)*i_h2 i_h2 += i_h/2 print(4*i_h) print(4*i_h2) print(np.abs(4*(i_h - i_h2))) print(np.abs((i_h - i_h2))/15) print("") #print(n_points) #h = xx[1]-xx[0] print(f'По формуле трапеций:') print(f'Шаг: {h}') print(f'Значение: {4*i_h2}') print(f'Разница с реальным значением: {np.abs(4*i_h2 - np.pi)}') #print(f'Разница между шагами: {np.abs(4*(i_list[0] - i_list[1]))}\n') def simpson4(f, a, b): h = 1 i_list = [0, 1] count = 2 while np.abs((i_list[0] - i_list[1]))/15 > 10**(-6): i_list = [0, 0] for i in range(len(i_list)): if i==1: h=h/2 n_points = int((b-a)/h) + 1 xx = np.linspace(a, b, n_points) xx.tolist() for j in range(1, len(xx) - 1): i_list[i] += f(xx[j]) i_list[i] = 2*i_list[i] + f(xx[0]) + f(xx[len(xx) - 1]) for j in range(len(xx) - 1): i_list[i] += 4*f((xx[j] + xx[j+1])/2) i_list[i] = i_list[i]*(h/6) #print(n_points) #h = xx[1]-xx[0] print(f'По формуле Симпсона:') print(f'Шаг: {h}') print(f'Значение: {4*i_list[1]}') print(f'Разница с реальным значением: {np.abs(4*i_list[1] - np.pi)}') #print(f'Разница между шагами: {np.abs(4*(i_list[0] - i_list[1]))}\n') x = sp.symbols('x') a = 0 b = 1 eps = 10**(-6) ff = 1/(1+x**2) #trapezoid4(f, a, b) simpson3(f, a, b) simpson4(f, a, b)

По формуле Симпсона: Шаг: 0.25 Значение: 3.141592502458707 Разница с реальным значением: 1.5113108631226169e-07 Разница между шагами: 2.3875007726825714e-05 По формуле Симпсона: Шаг: 0.25 Значение: 3.141592502458707 Разница с реальным значением: 1.5113108631226169e-07

Контрольные вопросы

1

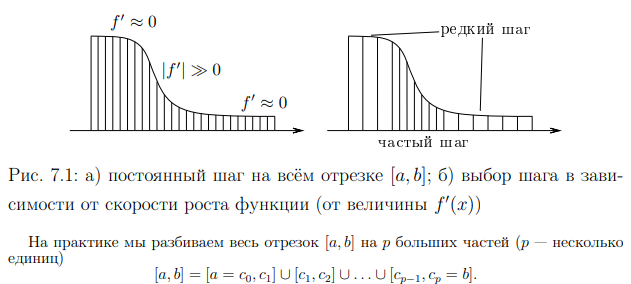
2

3

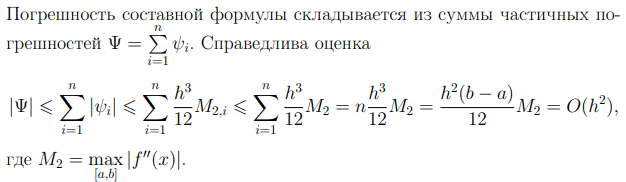
Метод прямоугольников

4