ЛР4, В15

import numpy as np import sympy as sp from sympy import * import matplotlib.pyplot as plt from scipy.optimize import root_scalar import math

1.1

def f(x): return np.e**(2*x) def derivate(f, x, eps): h = 1 d11 = 2 d12 = 1 while np.abs((d12 - d11)) > eps: d11 = (f(x) - f(x - h)) / h h = h/2 d12 = (f(x) - f(x - h)) / h h = 1 d21 = 2 d22 = 1 while np.abs((d22 - d21)) > eps: d21 = (f(x + h) - f(x - h)) / (2 * h) h = h/2 d22 = (f(x + h) - f(x - h)) / (2 * h) return d11, d21 eps1 = 10**(-3) eps2 = 10**(-6) x0 = 1.5 d11, d21 = derivate(f, x0, eps1) d12, d22 = derivate(f, x0, eps2) print("Точность: ", eps1) print("\tПо первой формуле:", d11) print("\tПо второй формуле:", d21) print("") print("Точность: ", eps2) print("\tПо первой формуле:", d12) print("\tПо второй формуле:", d22)

Точность: 0.001 По первой формуле: 40.169847947428934 По второй формуле: 40.17148248891726 Точность: 1e-06 По первой формуле: 40.171072602272034 По второй формуле: 40.171074245430646

2.1

def f(x): return np.e**(2*x) def derivateOne(f, x, h): d1 = (f(x) - f(x - h)) / h return d1 def derivateTwo(f, x, h): d2 = (f(x + h) - f(x - h)) / (2 * h) return d2 def Oh(ff, h, x0, x): #d1 = np.abs(sp.diff(sp.diff(ff, x), x).subs(x, x0)) #d2 = np.abs(sp.diff(sp.diff(ff, x), x).subs(x, x0-h)) # m = 0 # xx = np.linspace(x0-h, x0+h, 100) # for i in xx: # d = np.abs(sp.diff(sp.diff(ff, x), x).subs(x, i)) # if d > m: # m = d #max_d = max(d1, d2) M2 = np.abs(sp.diff(sp.diff(ff, x), x).subs(x, x0+h)) return M2 * h / math.factorial(2) def Oh2(ff, h, x0, x): M3 = np.abs(sp.diff(sp.diff(sp.diff(ff, x), x), x).subs(x, x0+h)) return M3 * h**2 / math.factorial(3) #h = [1/2, 1/4, 1/8, 10**(-3), 10**(-6)] #h = [1/2, 1/4, 1/8] h = [] for i in range(3, 101): h.append(1/2**i) #h = [1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, 1/1024] #h=np.linspace(1,1/2048,11) #h.tolist() # print(h) x0 = 1.5 x = sp.symbols('x') ff = np.e**(2*x) ohList = [] for hi in h: ohList.append(Oh(ff, hi, x0, x)) #print(ohList) print("") oh2List = [] for hi in h: oh2List.append(Oh2(ff, hi, x0, x)) #print(oh2List) plt.plot(h, ohList, 'bo', label = 'Oh') #plt.plot(h, oh2List, 'ro', label = 'Oh2') plt.xlabel('h') plt.ylabel('Oh') plt.legend() plt.grid() plt.show()

plt.plot(h, oh2List, 'ro', label = 'Oh2') plt.xlabel('h') plt.ylabel('Oh2') plt.legend() plt.grid() plt.show()

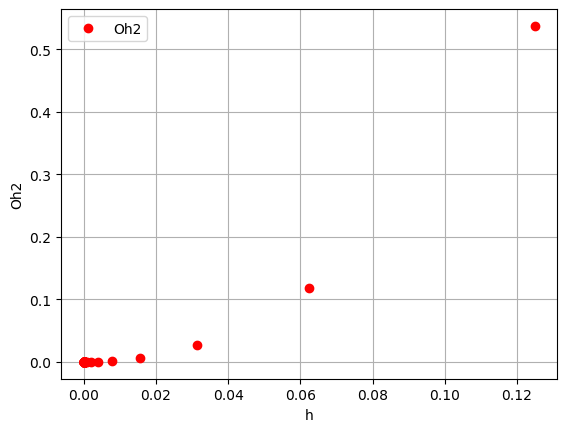
При формуле с первым порядком погрешности погрешность уменьшается во столько раз, во сколько и шаг. Пример: шаг: h, погрешность: eps; шаг: h/2, погрешность: eps/2; шаг: h/4, погрешность: eps/4

При формуле со вторым порядком погрешности погрешность уменьшается в квадрат раз больше, во сколько шаг. Пример: шаг: h, погрешность: eps; шаг: h/2, погрешность: eps/4; шаг: h/4, погрешность: eps/16

3.1

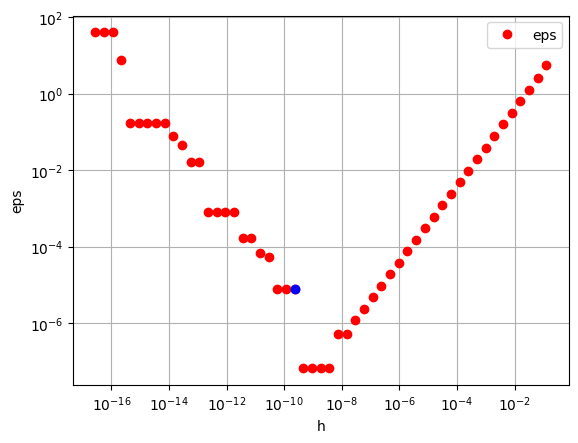
def f(x): return np.e**(2*x) def derivate(f, x, h): d = (f(x + h) - f(x)) / h return d def Oh(ff, h, x0, x): M2 = np.abs(sp.diff(sp.diff(ff, x), x).subs(x, x0+h)) return M2 * h / math.factorial(2) h = [] for i in range(3, 56): h.append(1/2**i) #print(h) x0 = 1.5 x = sp.symbols('x') ff = np.e**(2*x) eps = [] for i in range(len(h)): eps.append(np.abs(sp.diff(ff, x).subs(x, x0) - derivate(f, x, h[i]).subs(x, x0))) ohList = [] for hi in h: ohList.append(Oh(ff, hi, x0, x)) i_h = 0 for i in range(len(eps) - 1): print(f'{i+1}:\n\t{h[i]}\n\t{eps[i]}\n') if eps[i] < eps[i+1]: print(f'Увеличение началось с {i+2} шага\n') print(f'{i+2}:\n\t{h[i+1]}\n\t{eps[i+1]}\n') i_h = i+1 break # print(" ") # for i in range(len(eps)): # print(f'{i+1}: {eps[i]}') plt.plot(h, eps, 'ro', label = 'eps') plt.plot(h[i_h], eps[i_h], 'bo') #plt.plot(h, ohList, 'bo', label = 'Oh') plt.xscale('log') plt.yscale('log') plt.xlabel('h') plt.ylabel('eps') plt.legend() plt.grid() plt.show()

1: 0.125 5.46735010566783 2: 0.0625 2.61865687904960 3: 0.03125 1.28191290356627 4: 0.015625 0.634262690649813 5: 0.0078125 0.315477484629774 6: 0.00390625 0.157327697883339 7: 0.001953125 0.0785613887746521 8: 0.0009765625 0.0392551168606232 9: 0.00048828125 0.0196211687343393 10: 0.000244140625 0.00980898752273873 11: 0.0001220703125 0.00490409461595931 12: 6.103515625e-05 0.00245194756822542 13: 3.0517578125e-05 0.00122594882665084 14: 1.52587890625e-05 0.000612968256938018 15: 7.62939453125e-06 0.000306482570486821 16: 3.814697265625e-06 0.000153240891414441 17: 1.9073486328125e-06 0.0000766200518782512 18: 9.5367431640625e-07 0.0000383110290940181 19: 4.76837158203125e-07 0.0000191555863793269 20: 2.384185791015625e-07 0.00000957413973168286 21: 1.1920928955078125e-07 0.00000477596582726392 22: 5.960464477539063e-08 0.00000239178003624829 23: 2.9802322387695312e-08 0.00000125929178551587 24: 1.4901161193847656e-08 5.44036048211183E-7 25: 7.450580596923828e-09 5.44036048211183E-7 26: 3.725290298461914e-09 6.71988900080578E-8 27: 1.862645149230957e-09 6.71988900080578E-8 28: 9.313225746154785e-10 6.71988900080578E-8 29: 4.656612873077393e-10 6.71988900080578E-8 Увеличение началось с 30 шага 30: 2.3283064365386963e-10 0.00000769659342125806

Контрольные вопросы

1

2

3

4

5