
ЛпМА_Бесов
.pdf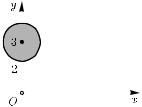
282 |
Гл. 19. Кратные интегралы |
8 ; 1 , ... ,
1
называется интегральной суммой Римана функции .
Определение 4. Интегралом Римана функции по измеримому множеству называется такое число , для которого
|
|
0 Æ Æ 0 |
|
1 |
|
при любом разбиении 6 множества с мелкостью 6 Æ и при любом выборе отмеченных точек , 1, ..., .
При этом функцию называют интегрируемой по Риману на множестве .
Интеграл от функции по множеству обозначается символами
+ , |
... 1, ... , + 1 ... + |
Кратко можно записать
+ |
8 |
|
; 1 , ... , , |
0 |
|
1 |
вкладывая в понятие предела тот смысл, который в определении 4 выражен в ( , Æ)-терминах.
|
|
|
|
Интеграл |
+ называется кратным интегралом при |
|||
2 (двойным интегралом при 2, тройным интегралом |
||||||||
|
|
|
|
|
|
|
при 3). |
|
|
|
|
|
|
|
|
Напомним, что в случае 1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
необходимым условием интегрируемости |
|
|
|
|
|
|
|
|
функции на отрезке является ограничен- |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ность этой функции на этом отрезке. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Следующий пример показывает, что при |
|
|
|
|
|
|
|
|
2 условие ограниченности функции |
|
|
|
|
|
|
|
|||
|
|
|
|
Рис. 1 |
|
|
не является необходимым для интегри- |
|
|
|
|
|
|
|
руемости этой функции. |
||
|
|
|
|
|
|
|
||
|
|
|
|
Пример 1. При 2 рассмотрим множество , имеющее |
||||
вид «шарика на нитке» (рис. 1): |
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 0, 3 |
0 0, 2 |
|

§ 19.1. Кратный интеграл и критерий интегрируемости |
283 |
и функцию : |
, |
|
|
|
|
|
|
1 |
при 0 1, |
||
|
|
|
|||
|
, |
|
|||
|
|
||||
|
0 при 1 |
||||
Ясно, что неограничена на |
, но |
, + + 0. |
|||
Однако если функция интегрируема на множестве , |
|||||
то она заведомо ограничена на внутренности (в частности, интегрируемая на открытом множестве функция ограничена на нём). Это утверждение вытекает из свойства 2Æ § 19.2 и из следующей теоремы, показывающей, что для измеримых множеств с некоторым дополнительным свойством интегрируемость функции влечёт её ограниченность.
Теорема 1. Пусть для множества существует такая по-
следовательность разбиений 6 , 6 0 при , для
1
которой все элементы всех разбиений имеют положительную меру. Пусть функция интегрируема на .
Тогда ограничена на .
Д о к а з а т е л ь с т в о по существу такое же, как в одномерном случае для , .
Упражнение 1. Пусть измеримое множество . Доказать, что всякая интегрируемая на функция ограничена на .
Напомним, что колебанием функции на множестве называется число
F ; |
|
|
|
|
, - |
|
|
- - |
|
Теорема 2 (критерий интегрируемости функции). Для ин- |
||||
тегрируемости функции на |
измеримом |
множестве |
||
необходимо и достаточно, чтобы |
|
|
|
|
0 Æ Æ 0 F |
6 6 Æ, (1) |
|||
1 |
|
|
|
|
. /0 |
|
|
|
|
где F F ; , 6 |
|
— разбиение множества . |
||
|
1 |
|
|
|
До к а з а т е л ь с т в о то же, что и для случая 1,
, в п. 14.2.1.
Критерий интегрируемости функции можно записать так:
|
F 0, |
(2) |
0 |
|
|
|
1 |
|
. /0

284 Гл. 19. Кратные интегралы
вкладывая в понятие предела тот смысл, который в (1) выражен в ( , Æ)-терминах.
Определение 5. Пусть функция определена на измеримом
множестве , и пусть 6 — разбиение . Пусть |
||||
также |
|
1 |
||
|
|
|
|
|
|
, |
|
||
Тогда суммы |
|
|
||
|
|
|
|
|
|
|
|
||
8 |
, |
|
8 |
|
1 |
1 |
|||
называют соответственно нижней и верхней интегральными суммами Дарбу функции , отвечающими разбиению 6.
Ясно, что для любой интегральной суммы Римана 8 ограниченной функции
8 8 8
Легко видеть, что
8 8 F
1
Спомощью последнего равенства и критерия интегрируемости (1) можно сформулировать критерий интегрируемости функции в терминах сумм Дарбу.
Теорема 3. Для интегрируемости на измеримом множествеограниченной функции необходимо и достаточно, чтобы
0 Æ Æ 0 8 8 6 6 Æ
Следствие 1. Пусть функция интегрируема на множестве. Тогда
8 + 8 ,
|
|
|
|
|
|
причём |
|
|
|||
|
0 Æ Æ 0 |
|
8 6 6 Æ |
||
|
8 |
||||
|
Покажем, что функция, интегрируемая на |
отрезке , |
|||
в |
смысле определения 14.1.2, интегрируема на |
этом |
отрезке |
||
и |
в смысле определения 4 ( 1, , ), |
так |
что эти |
||
два определения (интегрируемости функции на отрезке) эквивалентны.
§ 19.1. Кратный интеграл и критерий интегрируемости |
285 |
Пусть функция интегрируема на отрезке , в смысле определения 14.1.2. Тогда она ограничена (по теореме 14.1.1), и в силу критерия интегрируемости 14.2.1 для заданного 0
существует разбиение 1, отрезка , такое, что
1
|
|
F ; 1, |
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
Пусть |
6 |
— произвольное |
разбиение |
отрезка |
, , |
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
60 — совокупность тех множеств 6, которые имеют непустое |
|||||||||||
пересечение более чем с одним отрезком 1, . Если 60, |
|||||||||||
то в силу леммы 18.2.1 |
2 |
|
, где |
0 |
, |
0 |
0. |
||||
|
|
|
|
0 |
|
|
0 |
|
|||
Теперь, считая, что на |
, , имеем |
|
|
|
|
||||||
F ; F ; F ; |
|||||||||||
1 |
0 |
|
|
|
|
0 |
|
|
|
||
|
F ; |
1, |
2 2 0 2 , |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
причём последняя оценка имеет место для всех разбиений 6 с достаточно малой мелкостью 6 по лемме 18.2.3. В силу критерия интегрируемости (теорема 2) функция интегрируема на , в смысле определения 4.
Установим условия интегрируемости непрерывных функций.
Теорема 4. Пусть функция непрерывна на измеримом компакте . Тогда интегрируема на .
Д о к а з а т е л ь с т в о. Функция в силу теорем Вейерштрасса и Кантора ограничена и равномерно непрерывна на компакте . Тогда её модуль непрерывности на F Æ; 0 при Æ 0. Следовательно,
|
F |
F 6 ; F 6 ; 0 при 6 0 |
1 |
1 |
|
В силу критерия интегрируемости функция интегрируема на .
Теорема 5. Функция, непрерывная и ограниченная на открытом измеримом множестве, интегрируема на нём.
У к а з а н и е. Для доказательства можно воспользоваться критерием интегрируемости функции и леммой 18.2.3; см. доказательство теоремы 14.2.4.
286 |
Гл. 19. Кратные интегралы |
§19.2. Свойства кратного интеграла
1.Пусть — измеримое множество. Тогда
+ 1 +
2.Пусть и — измеримые множества, , и пусть функция интегрируема на . Тогда она интегрируема и на .
Д о к а з а т е л ь с т в о. |
Пусть |
6 |
|
|
— разбиение |
||||
множества |
|
мелкости |
6 . Дополним 6 |
1 |
до разбиения |
||||
|
множества мелкости 6 6 . Это можно сделать, |
||||||||
6 1 |
|
|
|
|
|
|
|
|
|
присоединив к |
|
|
все элементы |
какого-либо разбиения |
|||||
множества |
|
|
1 |
мелкостью |
разбиения, |
не превосходя- |
|||
|
с |
||||||||
щей 6 . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
F |
||||
|
1 |
|
|
1 |
|
|
|
||
|
. /0 |
|
|
. /0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Из интегрируемости функции на и критерия интегрируемости следует, что правая часть последнего неравенства стремится к нулю при 6 0. Поэтому и левая часть стремится к нулю при 6 0. В силу критерия интегрируемости функция интегрируема на .
3 (аддитивность интеграла по множествам). Пусть множе-
ства /, C измеримы, |
причём / C , / C. |
|
Пусть функция : |
ограничена и интегрируема на / и на |
|
C. Тогда интегрируема на и |
||
+ + + |
||
|
" |
0 |
Д о к а з а т е л ь с т в о. Пусть 6 — разбиение множества , 60 — множество тех 6, для которых / ,
C ,
6 / / 6, / , 6 C C 6, C
Пусть 8 — произвольная интегральная сумма Римана функции и разбиения 6 множества с отмечен-
ными точками , 1, ..., . Пусть 8 " , 8 0 — интегральные суммы для сужений функции на множества /
и C соответственно, построенные по разбиениям 6 / и 6 C
§ 19.2. Свойства кратного интеграла |
287 |
и (по возможности) по тем же отмеченным точкам, что и 8 . Тогда, считая, что на , имеем
8 8 " 8 0 2 2 ' |
(1) |
||
|
0 |
0 |
|
Заметим, что если 60, то |
|
|
|
|
2 D/ |
|
(2) |
В самом деле, пусть |
/, C. Тогда на отрезке, |
||
соединяющем точки |
и , по лемме 18.2.1 найдётся точка . |
||
D/. Тогда . 6 .
Поскольку D/ 0 в силу критерия измеримости, то из (2) и из леммы 18.2.3 следует, что правая часть (1) стремится к нулю при 6 0. Тогда и левая часть (1) стремится к нулю. Так как
8 " |
+ , |
8 0 |
+ , |
|
" |
|
0 |
то заключаем, что |
8 |
" + |
0 + , откуда |
и следует свойство 3. |
|
|
|
Упражнение 1. |
Показать, |
что требование ограниченности |
|
функции на множестве в формулировке свойства 3 нельзя отбросить.
4.Пусть функция интегрируема и ограничена на множестве
. При изменении её значений на подмножестве 0 меры 0 (с сохранением ограниченности) функция остаётся интегрируемой и величина интеграла не изменяется.
Д о к а з а т е л ь с т в о.
+ + + +
0 0 0
Следовательно, интегрируемость функции и значения интеграла + не зависят от значений функции на 0.
Следствие 1. Пусть функция определена и ограничена на замыкании измеримого множества . Тогда интегралы
+ , |
+ , |
+ |
|
|
|
|
|
|
|
||
существуют или не существуют одновременно и равны в случае их существования.

288 Гл. 19. Кратные интегралы
5 (линейность интеграла). Пусть функции , # интегрируемы на множестве , и пусть , . Тогда существует интеграл
# + + # +
|
|
|
|
6. |
Пусть функции , # интегрируемы и ограничены на . |
||
Тогда |
их произведение #, а если # |
0, то и частное |
|
интегрируемы на . |
|
|
|
|
|
||
7. |
Пусть функция интегрируема на . Тогда функция |
||
интегрируема на и при этом |
|
|
|
+ +
8 (интегрирование неравенств). Если функции , # интегрируемы на и # на , то
+ # +
9 (полная, или счётная аддитивность интеграла по множествам). Пусть функция интегрируема и ограничена на мно-
жестве , а |
— последовательность измеримых множеств |
||||
|
|
1 |
|
|
|
со свойством |
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
Тогда |
|
+ |
|
|
+ . |
|
|
|
|
|
|
Д о к а з а т е л ь с т в о следует из оценки |
|||||
+ |
|
+ |
+ |
||
|
|
|
|
|
|
10. Пусть функция интегрируема и неотрицательна на открытом множестве C. Пусть непрерывна в точке 0 C
и 0 0. Тогда |
0 |
+ |
0. |
Д о к а з а т е л ь с т в о. В силу непрерывности функции |
|||
в точке 0 существует окрестность Æ 0 C такая, что |
|||
0 |
0 |
||
|
|
2 |
Æ |
§ 19.3. Сведение кратного интеграла к повторному |
289 |
Следовательно,
|
+ + + |
0 |
0 |
0 |
|
2 Æ |
|
||||
0 |
0 Æ 0 |
Æ 0 |
|
|
|
11 (теорема о среднем). Пусть функции , # интегрируемы и ограничены на множестве . Пусть функция # не меняет знака на . Если на , то существует такое число ), , что
# + ) # +
Если при этом — область, а функция непрерывна на , то
# + # + |
|
|
|
В частности, при # 1 |
|
+ |
|
|
|
Д о к а з а т е л ь с т в о основано на использовании свойства 8 и теоремы 10.5.4 (Коши о промежуточных значениях).
§ 19.3. Сведение кратного интеграла к повторному
|
|
Теорема 1. Пусть функция интегрируема по прямоуголь- |
||||||||||||||||||
нику % |
, , + 2 |
и |
интеграл / |
|
|
, + |
||||||||||||||
существует для каждого , + . |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Тогда функция / интегрируема по отрезку , + |
и справед- |
|||||||||||||||||
ливо равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, + |
|
+ |
|
|
, + |
+ |
|
|
|
(1) |
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правая часть равенства (1) называется повторным интег- |
||||||||||||||||||
ралом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Д о к а з а т е л ь с т в о. Пусть |
|
|
0 |
|
|
1 |
|
... |
||||||||||
|
|
, |
|
|
0 |
|
1 |
... |
+, |
6 |
1 |
|
, , |
|||||||
|
|
|
|
|
|
|
отрезков |
, |
и , + |
1 |
1 |
|||||||||
6 |
2 |
|
, — разбиения |
|
соответ- |
|||||||||||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ственно на отрезки. Тогда 6 1, |
1, |
|
1 — |
|||||||||||||||||
разбиение прямоугольника % на прямоугольники. |
|
|
1 |
|||||||||||||||||
10 О.В. Бесов

290 Гл. 19. Кратные интегралы
Введём обозначения
|
|
|
, |
|
|
|
|
1 |
, 1, |
1, 1, |
|
||
Тогда при 3 1, |
|
|
|
|
||
/ 3 , 3 + |
|
|
||||
1 |
1 |
|
|
|
||
|
|
|
|
|
, 3 + , |
|
|
|
|
|
1 1 1 |
|
|
откуда |
|
|
|
|
|
|
|
|
/ 3 |
(2) |
|||
1 1 |
|
1 |
|
1 1 |
|
|
Левая и правая части неравенств (2) представляют собой соответственно нижнюю 8 и верхнюю 8 интегральные
суммы Дарбу функции . При 6 |
0 каждая из них стре- |
|
мится к |
1 , + + (см. следствие из теоремы 19.1.3). |
|
Следовательно, средняя часть неравенств (2), представляющая собой интегральную сумму Римана 8 2 / , имеет предел при
6 |
|
0, являющийся по определению интегралом |
/ + |
||||
|
2 |
|
|
|
|
|
|
|
|
|
, + +. Предельным переходом в неравенствах |
||||
|
|
|
|
|
|
|
|
(2) получаем (1). |
|
|
|
||||
|
|
Замечание 1. Заменой обозначения переменных в теореме 1 |
|||||
получаем следующее утверждение. |
|
||||||
|
|
Теорема 1 . Пусть функция интегрируема по прямоуголь- |
|||||
нику % , , + 2 |
и интеграл / |
, + |
|||||
существует для каждого |
|
, . |
|
||||
|
|||||||
|
|
Тогда функция / интегрируема по отрезку , и справед- |
|||||
ливо равенство |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
, + |
+ |
, + + |
(3) |
Если выполняются условия как теоремы 1, так и теоремы 1 ,
то
|
|
, + + |
, + + , + + |
1 |
|
|

|
§ 19.3. Сведение кратного интеграла к повторному |
291 |
||||||
Последняя формула справедлива, в частности, если функция |
||||||||
непрерывна на %. |
|
|
|
|
|
|
||
Распространим результаты теорем 1, 1 , полученные для пря- |
||||||||
моугольника %, на множества, которые назовём элементарными. |
||||||||
Определение 1. Множество |
|
|
|
|||||
|
|
, 2 |
|
|
, |
|
1 , |
(4) |
где функции |
, 1 непрерывны на , и |
1 на , , назовём |
||||||
элементарным относительно оси '. Заметим, что — изме- |
||||||||
римое замкнутое множество. |
|
|
|
|
|
|||
Теорема 2. Пусть множество элементарно относительно |
||||||||
оси ', функция интегрируема и ограничена на и при |
||||||||
каждом |
|
, существует интеграл , , +. |
|
|||||
Тогда |
|
|
|
|
|
|
||
|
|
|
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
, + |
+ |
|
|
, + + |
(5) |
|
|
|
|
|
|
|
|
|
|
Д о к а з а т е л ь с т в о. Положим |
|
|
|
|||||
|
|
|
, |
+ 1 |
|
|||
|
|
|
, |
|
|
, |
|
|
(рис. 1). Тогда % |
, , + . |
|
|
|
||||
|
|
|
|
Рис. 1 |
|
|
|
|
Рассмотрим функцию : % |
: |
|
, , |
при |
, , |
0 |
при |
, % . |
Так |
как функция интегрируема и ограничена на , то функ- |
|
ция |
, интегрируемая на и на % , интегрируема на %, |
|
причём |
1 , + + , + +. |
|
10*
