
ЛпМА_Бесов
.pdf
202 Гл. 14. Определённый интеграл
А это означает, что
2 0 |
0 при |
0 |
, , |
0, |
|
||||
что и требовалось доказать. |
|
|
|
|
Пусть функция интегрируема на , . Тогда на |
, опре- |
|||
делена функция |
|
|
|
|
|
C " +", |
, , |
|
|
называемая интегралом с переменным нижним пределом. Поскольку
C " +" / ,
|
|
|
то функция C непрерывна на |
, . Если же |
непрерывна |
в точке 0 , , то существует |
|
|
C 0 / |
0 0 |
(3) |
Как и раньше, через , будем обозначать промежуток (т. е. отрезок, интервал или какой-либо из полуинтервалов) с концами в точках , .
Теорема 3. Пусть функция непрерывна на промежут-
ке , . Тогда она имеет на , |
первообразную |
|
|||||
|
|
|
|
|
|
|
|
/ |
" +", |
где |
0 , |
|
|||
|
0 |
|
|
|
|
|
|
Д о к а з а т е л ь с т в о |
следует из (2) при |
, , |
0 |
||||
или из (3) при |
, , |
0, если учесть, что в последнем |
|||||
случае / можно представить в виде / |
0 " +". |
|
|||||
|
|
|
|
|
|
|
|
Теорема 4 (основная теорема интегрального исчисления). |
|||||||
Пусть функция непрерывна на отрезке |
, |
и < — её первооб- |
|||||
разная на этом отрезке. Тогда |
|
|
|
|
|
||
|
+ |
< < |
|
|
(4) |
||
Эта формула называется формулой Ньютона–Лейбница.
Д о к а з а т е л ь с т в о. Функция / " +" является |
||
первообразной для функции на отрезке , . |
Поэтому |
|
/ < $, |
|
|
|
§ 14.5. Замена переменного и интегрирование по частям |
203 |
|
Отсюда |
|
|
|
|
" +" / / < $ < $ |
|
|
|
< < , |
|
При последнее равенство совпадает с (4).
Значение формулы Ньютона–Лейбница состоит в том, что она связывает два понятия: неопределённого и определённого интегралов, которые были введены и изучались независимо. Она даёт возможность вычислить определённый интеграл, если найден неопределённый.
Упражнение 1. Пусть на , функция |
интегрируема |
и имеет первообразную /. Доказать, что |
+ / |
/ . |
|
§14.5. Замена переменного
иинтегрирование по частям
Теорема 1 (о замене переменного). Пусть функция непрерывно дифференцируема на отрезке , , а функция непре-
рывна на отрезке , , |
|
, . Тогда |
|
|
|
|
|
+ |
|
" " +" |
(1) |
До к а з а т е л ь с т в о. Пусть < — первообразная для на отрезке , . Тогда < — первообразная для на
отрезке , , поскольку < " " " , где производные при " и при " понимаются как односторонние
(см. теорему 5.5.1 и замечание 5.5.1). |
|
Дважды воспользовавшись формулой |
Ньютона–Лейбница, |
получаем (при любом расположении точек |
и ) |
+ < < ,
" " +" < < < <
Из этих двух равенств вытекает утверждение теоремы.
204 |
Гл. 14. Определённый интеграл |
Упражнение 1. Доказать, что если функция непрерывна |
|
на , , |
0 на , , , , то из существова- |
ния одного из интегралов формулы (1) следуют существование другого и равенство (1).
Теорема 2 (интегрирование по частям). Пусть функции 0, =
непрерывно дифференцируемы на отрезке |
, . Тогда |
|
||
0 |
= + 0 = 0 |
= + , |
(2) |
|
|
|
|
|
|
|
|
|
||
где 0 = |
0 = 0 = . |
|
|
|
Д о к а з а т е л ь с т в о. Из равенства |
|
|
||
0 = 0 = 0 = , |
, |
|
||
следует |
|
|
|
|
0 = + 0 = + |
0 = + |
|
||
|
|
|
|
|
Остаётся заметить, что по формуле Ньютона–Лейбница |
|
|||
0 = + 0 = 0 = |
|
|||
|
|
|
|
|
Определение 1. Функция : , |
называется непрерыв- |
|||
ной и кусочно-непрерывно дифференцируемой, или непрерывной и кусочно-гладкой, на отрезке , , если она непрерывна
на , и существует разбиение отрезка , , при котором
0
производная непрерывна на каждом отрезке 1, , если в его концах производную понимать как одностороннюю.
Обобщим понятие определённого интеграла.
Определение 2. Интегралом по отрезку , функции , определённой на отрезке , за исключением конечного числа точек, называется число
+ + ,
если стоящий справа интеграл существует. Здесь : , — функция , каким-либо образом доопределённая в этих точках.

|
§ 14.6. Приложения определённого интеграла |
205 |
|
Интеграл + определён здесь корректно, так |
как |
+ не зависит от способа доопределения функции , что |
||
следует из свойства 8 интеграла. |
|
|
Теорема 3 (интегрирование по частям). Пусть функции 0, =
непрерывны и кусочно-непрерывно дифференцируемы на отрезке , . Тогда справедлива формула (2).
Д о к а з а т е л ь с т в о. В силу определения 1 существует
разбиение отрезка , , при котором функции 0, = непре- |
|||
0 |
|
|
|
рывно дифференцируемы на каждом отрезке 1, ( 1, ... |
|||
... , ). Производные же 0 , = |
в точках ( 0, ... , ) могут не |
||
существовать. В силу определения 2 и свойства 8 интеграла |
|||
|
|
|
|
0 = + |
0 = + |
||
|
|||
|
1 1 |
||
Применяя к каждому слагаемому правой части теорему 2, получаем
0 = + |
|
|
|
|
0 = |
|
0 = + |
||
|
1 |
1 1 |
|
|
0 = +
§14.6. Приложения определённого интеграла
Вэтом параграфе будет показано, как с помощью определённого интеграла вычислить площадь криволинейной трапеции,
объём тела вращения и другие величины. Фигуру в 2 , имеющую площадь, называют квадрируемой, а тело в 3 , имеющее объём, — кубируемым. Обобщением этих понятий является понятие измеримого множества в ( ). Здесь же мы ограничимся лишь констатацией некоторых свойств измеримости (по Жордану) и (жордановой) меры, позволяющих вычислить меры (площади) плоских фигур и меры (объёмы) трёхмерных тел простых геометрических форм 1). Меру множества будем обозначать символом .
1) Ниже (гл. 18) будет показано, что такие множества измеримы (т. е. имеют меру).
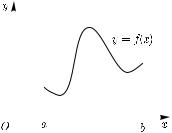
206 |
Гл. 14. Определённый интеграл |
|
|
Перечислим свойства меры, которые будут |
использованы |
в этом параграфе: |
|
|
|
а) если % — прямоугольный параллелепипед в , опреде- |
|
ляемый соотношениями |
|
|
|
1, 1 ... , % 1, 1 ... , , |
|
где |
(@ 1, ..., ), то % & |
; |
|
1 |
|
б) (монотонность меры) если множества 1, 2 измеримы, и 1 2, то 1 2;
в) (аддитивность меры) если множества 1, 2 измеримы, и 1 2 , то 1 2 1 2.
Из a) и б) следует, что 0 для всякого измеримого множества (неотрицательность меры).
Из б) и в) следует г) (полуаддитивность меры) если множества 1, 2 измери-
мы, то 1 2 1 2.
(I) Площадь криволинейной трапеции. Криволинейной
трапецией называется множество C 2 |
вида |
|
|||||||||||||||
|
|
|
C |
|
, 2 |
|
|
|
, |
0 , |
(1) |
||||||
где функция непрерывна на отрезке |
, , 0 на |
, . |
|||||||||||||||
|
Пусть 6 |
, |
|
0 |
|
1 |
... |
, |
, |
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
. |
1, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим две ступенчатые фи- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
гуры C 6 , C 6 следующим об- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
разом (рис. 1): |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C 6 |
|
1, 0, , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
'1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C 6 |
|
1, 0, |
||
Рис. 1
'1
Очевидно, C 6 C C 6 , откуда следует
C 6 C C 6

§ 14.6. Приложения определённого интеграла |
207 |
Поскольку
C 6 8 ,
1
C 6 8 ,
1
где 8 , 8 — соответственно наименьшая и наибольшая интегральные суммы Римана функции для разбиения 6, то
8 C 8
Отсюда, устремляя мелкость 6 разбиения 6 к нулю, получаем, что площадь криволинейной трапеции C равна
|
C |
+ |
|
|
|
|
Замечание 1. Аналогично показывается, что |
|
|
C + |
C C DC |
|
|
|
|
Упражнение 1. Выяснить геометрический смысл интеграла |
|
|
+ , где непрерывная на отрезке , функция отрица- |
|
тельна или меняет знак. |
|
|
|
Упражнение 2. Выразить с помощью определенных интегра- |
|
лов площадь круга радиуса ; и площадь его сектора. |
||
|
(II) Площадь криволинейного сектора. Пусть в полярной |
|
системе координат задана кривая |
|
|
7 , 2 2 , 2 ,
где функция 2 непрерывна и неотрицательна на ,0, 2- , C , 2 : 2 , 0 2 — криволинейный сектор.
Пусть 6 — разбиение отрезка , , , |
|
0 |
, |
1 |
|
. |
|
1, |
|
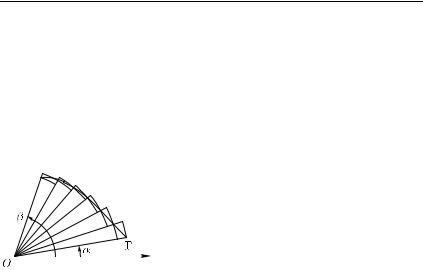
208 Гл. 14. Определённый интеграл
Построим две фигуры C 6 , C 6 (рис. 2):
|
|
C 6 |
, 2 2 , 0 , |
|
'1 |
|
|
C 6 |
, 2 2 , 0 |
|
'1 |
Тогда площадь криволинейного сектора C удовлетворяет двойному неравенству (см. упражнение 2)
|
|
1 |
|
|
2 C 6 C |
|
||||||
|
|
|
|
|
|
|||||||
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
C 6 |
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
||||
Рис. 2 |
Отсюда при 6 0 получаем, что пло- |
|||||||||||
щадь криволинейного сектора C равна |
||||||||||||
|
||||||||||||
|
C |
1 |
2 2 +2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|||||||
(III) Объём тела вращения. Множество 3 , определяемое соотношением
, , . 3 , 2 .2 ;2, , . 3 , 2 .2 ;2 ,
называется прямым круговым цилиндром.
Упражнение 3. Вывести формулу -;2 .
Пусть функция непрерывна и неотрицательна на отрез-
ке , , тело |
3 образовано вращением криволинейной |
|
трапеции (1) вокруг оси ' . |
||
Пусть 6 |
|
— разбиение отрезка , , , |
|
|
0 |
|
, |
1, |
|
|
|
1, |
|
|
|
|
, , . 3 1 , 2 .2 2 , |
6 |
|
|
|
'1 |
|
|
|
, , . 3 1 , 2 .2 2 |
6 |
|
|
'1

§ 14.6. Приложения определённого интеграла |
209 |
Тогда
|
|
|
|
- 2 |
6 |
6 - 2 |
|
1 |
|
1 |
|
Отсюда при 6 0 получаем, что объём тела вращения равен
- 2 +
(IV) Вычисление длины кривой. Пусть кривая 7 " :
" непрерывно дифференцируема.
Ранее было установлено, что непрерывно дифференцируемая кривая спрямляема (имеет длину) и что производная переменной длины дуги 9 " этой кривой
9 " "
Пусть 8 — длина кривой 7. Тогда
89 9 9 " +" " +"
2 " 2 " . 2 " +"
Если 7 , : — плоская кривая, то её длина равна
8 1 2 +
(V) Площадь поверхности вращения. Пусть функция
непрерывно дифференцируема и неотрицательна на отрезке , . Пусть 8 — поверхность, образованная вращением вокруг оси ' кривой 7 , : , т. е. графика функции . Площадь поверхности 8 (определение которой будет дано ниже) обозначим символом 8.
Пусть 6 , |
|
0 |
|
1 |
... — разбиение |
0 |
|
|
|
||
отрезка , . Построим вписанную в 7 ломаную 7 6 , соединив |
|||||
последовательно точки |
, |
, 0, 1, ... , , кривой 7 от- |
|||
резками. Поверхность, образованную вращением ломаной 7 6 вокруг оси ' , обозначим через 8 6 . Эта поверхность представляет собой объединение боковых поверхностей усечённых конусов или цилиндров, площади которых известны из курса

210 Гл. 14. Определённый интеграл
элементарной геометрии. Поэтому площадь поверхности 8 6 |
||||||||
равна |
|
|
|
|
|
|
||
|
|
|
|
1 4 , |
||||
|
|
|
8 6 - |
|||||
где |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
4 1 2 1 2 |
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
1 |
1 2 , (2) |
||||||
|
|
|
|
|
|
|
|
|
а точки 1, определяются формулой (6.1.3) конечных приращений Лагранжа.
Определение 1. Площадью поверхности 8 называется
8 8 6 , |
(3) |
0 |
|
если этот предел существует.
Покажем, что в рассматриваемом случае площадь поверхности 8 существует и равна
8 2- 1 2 + |
(4) |
Обозначим через G ; 1, ... , интегральную сумму Римана последнего интеграла, построенную по разбиению 6 и по тем же самым, что и в (2), отмеченным точкам 1, ..., . Тогда, полагая
1 , имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 $ |
|
|
|
$ |
|
|||||||||
8 6 2-G 2- |
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
6 1 2 |
|
|
||||||||||
1 |
|
2- |
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2- 1 1 |
2 |
|
|
|
|
0 при 6 0 |
||||||||||
|
|
|
1 |
6 |
||||||||||||||
Следовательно, и левая часть этой цепочки неравенств стре- |
||||||||||||||||||
мится к нулю при 6 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
G |
1 |
2 + |
при 6 |
0, |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поскольку подынтегральная функция непрерывна на , . Следовательно, существует предел (3), и справедливо равенство (4).
§ 14.7. Несобственные интегралы |
211 |
§ 14.7. Несобственные интегралы
Определение 1. Пусть функция : |
, , , ин- |
тегрируема по Риману на любом отрезке |
, , . |
Символ |
|
+ |
(1) |
называется несобственным интегралом (Римана) по полуинтервалу , . Говорят, что несобственный интеграл (1) сходится, и пишут
|
+ |
|
+ , |
(2) |
|
0 |
|
||
|
|
|
|
|
если указанный предел существует, и что несобственный интеграл (1) расходится в противном случае (здесь и далее символ0 равнозначен символу ).
Таким образом, в случае сходимости несобственным интегралом называют не только символ (1), но и его значение — число (2).
Сравним понятия интеграла Римана и несобственного интеграла Римана. Если , то функция задана на бесконечном промежутке, для которого интеграл Римана не определён, в то время как несобственный интеграл (2) может существовать. Если же , а функция неограничена на , , то интеграл Римана по , не существует, в то время как несобственный интеграл (2) может существовать.
Если функция интегрируема по Риману на отрезке , , то сходится и несобственный интеграл (2) по , причём эти
интегралы равны. Это следует из непрерывности + как функции аргумента в силу теоремы 14.4.1.
Упражнение 1. Доказать, что если функция ограничена на отрезке , и интегрируема по Риману на любом отрезке, , , то она интегрируема по Риману на , , и, следовательно, её интеграл Римана по , и несобственный интеграл по , совпадают.
У к а з а н и е. Воспользоваться критерием интегрируемости функции.
Таким образом, понятие несобственного интеграла шире понятия интеграла Римана.
Замечание 1. Если верхний предел несобственного интеграла равен , то вместо символа часто пишут .
