
ЛпМА_Бесов
.pdf
92 Гл. 7. Исследование поведения функций
Д о к а з а т е л ь с т в о (для случая выпуклости вверх). До-
статочность. При |
|
|
|
имеем, используя (1) |
|||||
и формулу конечных приращений Лагранжа, |
|
|
|
||||||
|
|
|
$ |
|
|
' |
|
|
|
4 , |
|
|
|
|
|
|
|
|
|
) $ |
' 0 |
0 при 5 0 , |
|||||||
|
|
|
|
|
|
|
|
|
|
где 5 3 . |
|
|
|
|
|
||||
Отсюда следует достаточность в утверждении 1Æ и утверждение 2Æ.
Упражнение 2. Доказать необходимость условия 1Æ. Можно использовать при этом анализ расположения кривой относитель-
но касательной, который будет приведен ниже. |
|
|||
Определение 2. Точка |
0 называется |
точкой |
перегиба |
|
функции , а точка 0, |
0 — точкой |
перегиба |
графика |
|
функции , если: |
|
|
|
|
1Æ существует производная 0 (конечная или бесконеч- |
||||
ная); |
|
|
|
|
2Æ точка |
0 является концом интервала строгой выпуклости |
|||
вверх и концом интервала строгой выпуклости вниз. |
|
|||
Напомним, что при выполнении условия 1Æ функция непре- |
||||
рывна в точке |
0. |
|
|
|
Теорема 2 (необходимые |
условия точки перегиба). Пусть |
|||
0 — точка перегиба функции , причём |
непрерывна в точке |
|||
0. Тогда |
0 0. |
|
|
|
Д о к а з а т е л ь с т в о проведём от противного. Допустим, что 0 0 и для определённости 0 0. Тогда 0 на некоторой окрестности 0 . По предыдущей теореме точка 0 находится внутри интервала 0 строгой выпуклости вниз
и поэтому не может быть точкой перегиба.
Теорема 3 (достаточные условия точки перегиба). Пусть существует 0 , а меняет знак при переходе через точку 0.
Тогда 0 — точка перегиба функции .
Д о к а з а т е л ь с т в о сводится к проверке определения точки перегиба с помощью теоремы о достаточных условиях строгой выпуклости функции.
Следствие. Пусть 0 0, 0 0. Тогда 0 — точка перегиба функции .
§ 7.3. Асимптоты |
93 |
Теорема 4 (о расположении графика функции относительно касательной).
1.Æ Если 0 0 ( 0 0), то 0 : график функциилежит строго выше (строго ниже) касательной
|
0 0 |
0 при |
|
0 . |
|||
2.Æ |
Если |
0 |
0, |
0 |
0, то 0 : график функции |
||
|
переходит через касательную, т. е. при 0 и при |
||||||
|
0 |
( |
|
0 ) лежит строго по разные стороны от каса- |
|||
тельной. |
|
|
|
|
|
||
Д о к а з а т е л ь с т в о аналогично доказательству теоремы 7.1.4. Утверждение 1Æ следует из формулы Тейлора
|
|
|
|
|
|
|
|
|
0 0 0 2 |
0 |
|||
а утверждение 2Æ — из формулы Тейлора |
||||||
|
|
0 |
|
0 0 |
0 |
|
|
3 |
|
||||
|
0 0 2 |
, |
|
0 0 3 |
, |
написанных для |
Æ 0 , где Æ 0 достаточно мало. |
||
|
§ 7.3. Асимптоты |
|
|
Определение 1. Пусть функция определена на , . |
|||
Прямая |
называется асимптотой (или |
наклонной |
|
асимптотой) графика функции при |
, если |
||
* 1 при |
|
|
|
Аналогично определяется (наклонная) асимптота при |
. |
||
Теорема 1. Для того чтобы график функции имел принаклонную асимптоту , необходимо и доста-
точно, чтобы
|
, |
|
|
|
|
Д о к а з а т е л ь с т в о |
предлагается провести в качестве |
|
упражнения.
Аналогично формулируется теорема о существовании (на-
клонной) асимптоты при |
. |
Определение 2. Прямая |
0 называется вертикальной |
асимптотой графика функции , если хотя бы один из пределов0 0 , 0 0 существует и равен или .

94 Гл. 7. Исследование поведения функций
Упражнение 1. Выяснить наличие наклонных и вертикальных асимптот у графиков функций 2 ,
1 .
§ 7.4. Построение графика функции
Построение графика функции рекомендуется проводить по следующей схеме.
1Æ Найти область определения функции, точки разрыва.
2Æ Найти асимптоты.
3Æ Построить приблизительный график функции.
4Æ Найти первую и вторую производные.
5Æ Найти точки, в которых эти производные не существуют или равны нулю.
6Æ Составить таблицу изменения знаков первой и второй производных.
7Æ Найти области возрастания и убывания функции и точки экстремума.
8Æ Найти интервалы выпуклости вверх (вниз) функции, точки перегиба.
9Æ Найти точки пересечения графика функции с осью ' , вычислить значения функции в точках экстремума и в точках перегиба.
10Æ Построить уточнённый график функции.
|
|
|
|
|
|
|
2 |
|
|
Пример 1. Построить |
график |
функции |
|
||||
|
1 |
|||||||
|
2 |
|
2 |
|
|
|||
|
|
, |
|
. |
|
|||
|
1 2 |
|
|
|
||||
|
|
|
1 3 |
|
||||
Составляем таблицу в соответствии с приведенной схемой:
|
|
, 0 |
0 |
0, 1 |
1 |
1, 2 |
2 |
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
не сущ. |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не сущ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строго |
строгий |
строго |
не сущ. |
строго |
строгий |
строго |
|
|
возр. |
макс. |
убыв. |
|
убыв. |
мин. |
возр. |
|
|
|
|
|
|
|
|
|
|
|
выпуклость вверх |
точка |
выпуклость вниз |
||||
|
|
разр. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
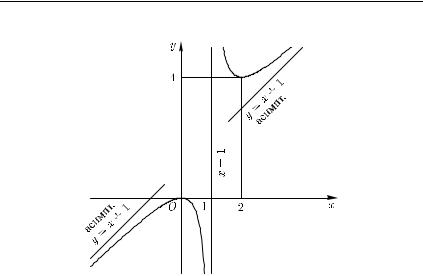
§ 7.4. Построение графика функции |
95 |
Построенный график функции изображен на рис. 1. |
|
Рис. 1 |
|

Г л а в а 8
КРИВЫЕ В ТРЁХМЕРНОМ ПРОСТРАНСТВЕ
§ 8.1. Векторнозначные функции
Определение 1. Пусть каждой точке " ! поставлен в соответствие вектор " трёхмерного пространства. Тогда будем говорить, что на ! задана вектор-функция (или векторная функция, или векторнозначная функция) .
Пусть в трёхмерном пространстве зафиксирована декартова прямоугольная система координат. Тогда " " , " , . " , где " , " , . " — координаты (компоненты) вектора " . Таким образом, задание на ! вектор-функции равносильно заданию на ! трёх числовых функций.
Символом обозначают длину вектора .
Определение 2. Вектор 0 |
называется |
пределом вектор- |
||
функции |
" при " |
"0 |
(пишут 0 |
" ), если |
" |
0 0. |
|
|
0 |
|
|
|
||
0 |
|
|
|
|
Как видим, в этом определении предполагается, что вектор-
функция " определена на некоторой окрестности "0 . Определение предела вектор-функции сведено к известно-
му определению предела числовой функции " " 0 . Написав последнее в ( -Æ)-терминах, приходим к иной форме определения предела вектор-функции.
Определение 3. Пусть вектор-функция " определена
на "0 . Вектор 0 называется пределом " при " "0, если
0 Æ Æ 0 " 0 " 0 " "0 Æ
Если " " , " , . " и 0 0, 0, .0 , то
" 0 " 0 2 " 0 2 . " .0 2
Из этого равенства видно, что существование предела "
0
0 равносильно существованию следующих трёх пределов чис-
ловых функций:
" 0, " 0, . " .0
0 |
0 |
0 |

§ 8.1. Векторнозначные функции |
97 |
Теорема 1. Пусть существуют пределы
1 " , |
2 " , |
" , |
0 |
0 |
0 |
где — числовая функция. Тогда существуют следующие пределы:
1Æ |
1 " 2 " 1 " 2 " ; |
||||||
|
0 |
|
0 |
|
0 |
|
|
2Æ |
" 1 " " |
|
1 " ; |
|
|||
|
0 |
|
0 |
0 |
|
|
|
3Æ |
|
" , |
" |
" , |
" ; |
||
|
1 |
2 |
|
1 |
|
2 |
|
|
0 |
|
0 |
|
0 |
|
|
4Æ |
" , " |
" , |
" 1). |
||||
|
1 |
2 |
1 |
|
2 |
|
|
|
0 |
|
0 |
|
0 |
|
|
Д о к а з а т е л ь с т в о. Эти свойства можно вывести из свойств числовых функций, перейдя к соответствующим равенствам для координат векторов.
Эти свойства можно доказать и непосредственно, опираясь на определение предела вектор-функции. Установим для примера свойство 4Æ. Пусть 1 " 10, 2 " 20. Тогда 1 "
0 |
0 |
10 α " , 2 " 20 |
β " , где α " , β " 0, 0, 0 при |
" "0. |
|
Имеем 1 " 2 " 10 20 10 α " 20 β "10 20 10 β " α " 20 α " β " при " "0,
так как
10 β " 10 β " 0, α " 20 α " 20 0,
α " β " α " β " 0
Определение 4. Пусть вектор-функция определена на"0 0 . Вектор 0 называют её пределом справа в точке "0, и пишут
|
|
|
0 |
" "0 0 , |
|
|
|
|
0 0 |
|
|
если |
" |
|
0 0. |
|
|
0 0 |
|
|
|
|
" "0 0 . |
Аналогично определяется предел слева |
|||||
|
|
|
|
0 0 |
|
Свойства 1Æ–4Æ верны и для односторонних пределов.
1) Наряду с обозначением 1, 2 для векторного произведения будет использоваться также 1 2.
4 О.В. Бесов
98 |
Гл. 8. Кривые в трёхмерном пространстве |
|
|
Определение |
5. Пусть вектор-функция определена |
на |
"0 . Она |
называется непрерывной в точке "0, если |
" "0 .
0
Из свойств пределов вектор-функций следует, что непрерывность вектор-функции равносильна непрерывности трёх числовых функций — её координат.
Теорема 2. Пусть вектор-функции 1, 2 и числовая функ-
ция непрерывны в точке "0. Тогда 1 2, 1, 1, 2 , 1, 2 непрерывны в точке "0.
Д о к а з а т е л ь с т в о следует из свойств пределов векторфункций.
Аналогично определению непрерывности даётся определение односторонней непрерывности. На этот случай переносятся и свойства, указанные в последней теореме.
Производная вектор-функции " , определённой на"0 , определяется как предел
"0 0 !0 ! !0 ,
0 !
если этот предел существует.
Если " " , " , . " , то, как легко видеть,
" " , " , . "
Односторонние производные вектор-функции определяются как соответствующие односторонние пределы отношения приращения вектор-функции к приращению аргумента.
Определение 6. Вектор-функция " , определённая на
"0 , называется дифференцируемой в точке "0, если существует такой вектор , что при " "0 " "0
"0 " "0 " ε " ",
где ε " при " 0.
Как и в случае числовых функций, показывается, что существование производной "0 и дифференцируемость в точке "0 — эквивалентные свойства и что "0 .
Дифференцируемость в точке "0 (существование "0 ) влечёт, очевидно, непрерывность в точке "0.
Дифференциалом вектор-функции в точке "0 называется линейная функция
+ "0 "0 +", +"

§ 8.1. Векторнозначные функции |
99 |
Теорема 3. Пусть в точке "0 существуют производные вектор-функций 1, 2 и числовой функции . Тогда в точке "0 существуют производные:
1Æ 1 2 1 2;
2Æ 1 1 1;
3Æ 1, 2 1, 2 1, 2 ; 4Æ 1, 2 1, 2 1, 2 .
Д о к а з а т е л ь с т в о приведём лишь для свойства 4Æ. Имеем
1 "0 " 2 "0 " 1 "0 2 "0
1 "0 " 1 "0 2 "0 "1 "0 2 "0 " 2 "0
Поделив обе части этого равенства на " и перейдя к пределу при " 0, получим 4Æ.
Выведем правило дифференцирования сложной вектор-функ-
ции " 6 , 6 60 .
Из равенства " 6 " 6 , " 6 , . " 6 дифференцированием получаем
! " 6 " 6 " 6 , " 6 " 6 , . " 6 " 6
" 6 " 6
Из этой формулы получаем выражение для дифференциала сложной вектор-функции
+ " +6 +"
Как видим, дифференциал + записывается в том же виде + +", как и в случае, когда " — независимое переменное. В этом состоит свойство инвариантности формы дифференциала первого порядка.
Производные высших порядков и дифференциалы высших порядков вектор-функций определяются аналогично тому, как это было сделано для числовых функций. Именно, " " и вообще " 1 " ,
+2 " Æ + " |
Æ |
Æ " +" |
" +"2, |
|
|
Æ |
|
|
|
и вообще |
|
|
|
|
+ " Æ + 1 " |
Æ 1 " +" 1 |
|
" +" |
|
Æ |
|
Æ |
|
|
4*

100 Гл. 8. Кривые в трёхмерном пространстве
Теорема 4 (формула Тейлора). Пусть существует "0 . Тогда существует окрестность "0 такая, что при " "0
" !0 " "0 ε " "0 " "0 ,
0 #
где ε " "0 при " "0.
Д о к а з а т е л ь с т в о. Каждую координату вектор-функции" " , " , . " заменим её разложением по формуле Тейлора. Полученное представление " запишем в виде суммы векторов, стоящих в правой части доказываемой формулы Тейлора.
Замечание 1. Модуль остаточного члена доказанной формулы Тейлора есть, конечно, * " "0 при " "0.
Определение 7. Вектор-функцию называют непрерывной
(дифференцируемой) на интервале или на отрезке, если она непрерывна (дифференцируема) в каждой точке интервала или соответственно отрезка. При этом непрерывность (дифференцируемость) в концах отрезка понимается как односторонняя.
Вектор-функцию называют непрерывно дифференцируемой в точке (на интервале, на отрезке), если непрерывна в точке (на интервале, на отрезке).
Мы видим, что многие свойства числовых функций переносятся на вектор-функции. Однако не так обстоит дело с формулой конечных приращений Лагранжа. В самом деле, пусть
" ", ", 0 , 0 " 2-. Тогда " ", ", 0 ,
" 1 и
2- 0 2- 0
ни при каком значении .
Справедлив, однако, векторный аналог оценки, вытекающей
из теоремы Лагранжа. |
|
|
|
Теорема 5. Пусть вектор-функция непрерывна |
на , |
||
и дифференцируема на , . Тогда |
, : |
|
|
|
|
|
(1) |
Д о к а з а т е л ь с т в о. |
Считая, что , |
положим |
|
. Тогда 1 и
, , ,
Рассмотрим функцию " " , . Для неё выполняются условия теоремы Лагранжа. Поэтому

§ 8.2. Кривая |
101 |
,
,
Отсюда следует утверждение теоремы.
§ 8.2. Кривая
Будем считать, что в трёхмерном пространстве 3 фиксирована декартова прямоугольная система координат.
Определение 1. Множество точек 7 3 с конкретным его описанием:
7 " , " , . " " ,
где , , . — непрерывные функции на , , называется (непрерывной) кривой.
Говорят ещё, что кривой называется «непрерывное отображение отрезка в пространство 3 ». На разъяснении этого понятия здесь останавливаться не будем.
Подчеркнём, что кривая определяется не только положением множества точек в пространстве 3 , но и способом его задания.
Ту же кривую 7 можно задать в виде
|
7 " " или 7 " |
" , |
где |
" " , " , . " — радиус-вектор |
точки " |
|
" , " , . " . Точкой кривой 7 называют пару ", " . |
|
Точка 3 называется кратной точкой (точкой самопе-
ресечения) кривой 7, если "1, "2 , , "1 "2: "1 "2
.
Кривая без кратных точек называется простой кривой (или
простой дугой).
Кривая 7 называется замкнутой кривой, или контуром, если . Контур называется простым контуром, если
из "1 "2 , "1 "2 следует "1 , "2 . Возрастание параметра " определяет некоторое направление
движения точки " по кривой (некоторый порядок прохождения точек кривой).
Поэтому говорят, что на кривой 7 задана ориентация, рассматриваемую кривую называют ориентированной кривой, точку — началом кривой, а точку — концом кривой.
Введём понятие касательной к кривой 7. Пусть "0, "0 ", . Проведём секущую через точки "0 , "0 " , и пусть
" — единичный вектор секущей, так что " , где
